
- •4.Энергетическая характеристика поля - потенциал. Потенциал точечного заряда. Принцип суперпозиции потенциалов.
- •5.Теорема о циркуляции вектора e.
- •6.Связь между напряженностью поля и разностью потенциалов
- •7.Силовые линии и эквипотенциальные поверхности. Свойства силовых линий.
- •8.Типы диэлектриков. Поляризованность.
- •9.Теорема Гаусса для вектора р.
- •10.Поведение вектора р на границе раздела двух сред.
- •12.Условия на границе раздела двух диэлектриков.
- •13.Поле внутри проводника. Статический случай.
- •14.Электроемкость уединенного проводника и конденсатора. Плоский конденсатор.
- •15.Электроемкость сферического конденсатора
- •16.Электроемкость цилиндрического конденсатора
- •17.Энергия взаимодействия зарядов
- •1 8.Энергия электрического поля (уединенный проводник, конденсатор).
- •19.Характеристики и условия существования электрического тока.
- •20.Уравнение непрерывности.
- •21.Закон Ома и закон Джоуля-Ленца в дифференциальной форме.
- •22.Классическая теория электропроводности
- •25.Виток с током в магнитном поле.
- •26.Линии вектора магнитной индукции. Теорема Гаусса для вектора в.
- •27.Теорема о циркуляции вектора Вв интегральной и дифференциальной формах.
- •28.Магнитное поле движущегося заряда.
- •2 9.Сила Лоренца.
- •30.Движение заряженной частицы в магнитном поле
15.Электроемкость сферического конденсатора
Н![]() айдем
разность потенциалов между обкладками
конденсатора, воспользуемся связью
между напряженностью и потенциалом:
айдем
разность потенциалов между обкладками
конденсатора, воспользуемся связью
между напряженностью и потенциалом:
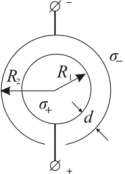
Н![]() апряженность
поля найдем с помощью теоремы Гаусса
апряженность
поля найдем с помощью теоремы Гаусса
![]()
![]()
![]()

Тогда

Е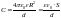
 сли
расстояние между обкладками мало п
по сравнению с
радиусами обкладок, то ф
формула переходит
в формулу для плоского конденсатора.d<<a,b
сли
расстояние между обкладками мало п
по сравнению с
радиусами обкладок, то ф
формула переходит
в формулу для плоского конденсатора.d<<a,b
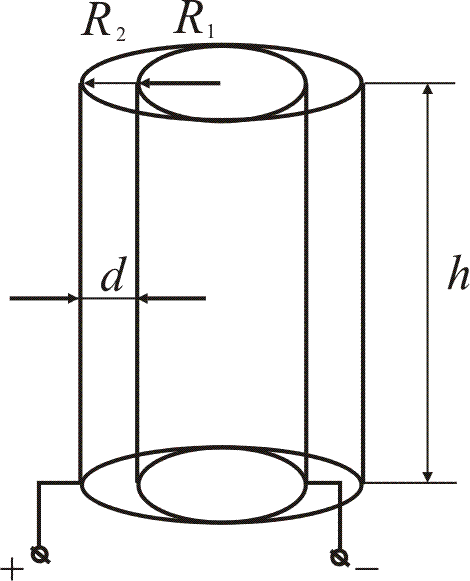
16.Электроемкость цилиндрического конденсатора
Расчет емкости проведем тем же способом, что и в случае сферического конденсатора:
![]()
![]()
![]()
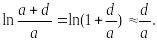
![]()

Еслиd<<a,b то
Приходим к формуле для плоского конденсатора:

17.Энергия взаимодействия зарядов
Р![]() ассмотрим
энергию взаимодействия двух зарядов,
которые в результате кулоновского
взаимодействия совершили перемещения
наПри этом силами поля совершена работа
ассмотрим
энергию взаимодействия двух зарядов,
которые в результате кулоновского
взаимодействия совершили перемещения
наПри этом силами поля совершена работа
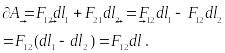
Работа равна убыли потенциальной энергии
![]()
Обобщая на систему зарядов
м ожно
записать для системы точечных зарядов:
ожно
записать для системы точечных зарядов:
г де
де
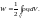
 потенциал,
создаваемый всеми остальными зарядами
системысистемыв
месте нахождения зарядаЕсли заряды
распределены непрерывно, то
потенциал,
создаваемый всеми остальными зарядами
системысистемыв
месте нахождения зарядаЕсли заряды
распределены непрерывно, то

-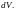 потенциал, создаваемый всеми зарядами
системы в элементе объема
потенциал, создаваемый всеми зарядами
системы в элементе объема
1 8.Энергия электрического поля (уединенный проводник, конденсатор).
Д ля
уединенного проводника:
ля
уединенного проводника:


Энергия взаимодействия не только обкладок между собой, но и
взаимодействия зарядов внутри каждой обкладки
Энергию системы зарядов можно выразить не только через заряд и потенциал, но и через характеристику поля – напряженность.
В случае плоского конденсатора
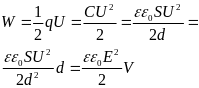
Э нергия
поля распределяется в пространстве с
объемной плотностью
нергия
поля распределяется в пространстве с
объемной плотностью
19.Характеристики и условия существования электрического тока.
Электрический ток – это упорядоченное движение носителей заряда.Для существования электрического тока необходимо:
наличие зарядов, способных перемещаться в пределах тела;
в проводнике должно существовать электрическое поле.
К оличественной
мерой тока служит сила
тока - заряд,
перенесенный через заданную поверхность
S (или через поперечное сечение
проводника), в единицу времени, т.е.:
оличественной
мерой тока служит сила
тока - заряд,
перенесенный через заданную поверхность
S (или через поперечное сечение
проводника), в единицу времени, т.е.:
За направление тока принято направление
движения положительных зарядов.
Э лектрический
ток может быть распределен по сечению
проводника неравномерно. Поэтому для
детальной характеристики тока вводят
вектор плотности тока j.Модуль
плотности
тока численно
равен заряду, переносимому через
единичную площадку, расположенную в
данной точке перпендикулярно направлению
движения носителей, за единицу времени
лектрический
ток может быть распределен по сечению
проводника неравномерно. Поэтому для
детальной характеристики тока вводят
вектор плотности тока j.Модуль
плотности
тока численно
равен заряду, переносимому через
единичную площадку, расположенную в
данной точке перпендикулярно направлению
движения носителей, за единицу времени
Плотность тока и сила тока
с вязаны
соотношением
вязаны
соотношением
