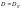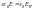10.Поведение вектора р на границе раздела двух сред.

Р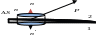 ассмотрим поведение вектора P на границе раздела двух диэлектриков. В качестве гауссовой поверхности возьмем небольшой цилиндр. Высоту цилиндра будем считать пренебрежимо малой, а ΔS настолько малой, чтобы вектор P для каждой точки ΔS можно было бы считать одинаковым. Нормаль к поверхности всегда будем проводить от первого диэлектрика ко второму.

П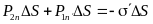 ренебрегая потоком через боковую поверхность, запишем

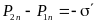
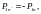
У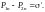 читывая, что получим

Или

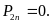
Е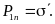 сли 2-ая среда вакуум,

С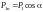 ледовательно Знак проекции

о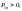 пределяет и знак

Е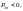 сли то на поверхности диэлектрика находится поло-

жительный заряд , если же то отрицательный.

11.Вектор электрического смешения D. Теорема Гаусса для вектора D. Рассмотрим теорему Гаусса для электростатического поля, которое в общем случае создается как свободными, так и связанными зарядами.

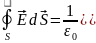
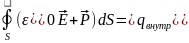
q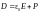 внутр – это свободные заряды, которые в дальнейшем будем называть сторонними. Величину

называют вектором электрического

смещения. В отличие от вектора напряженности электрического поля, вектор электрического смещения физического смысла не имеет. Он вводится для удобства расчета полей в средах.

Приходим к теореме Гаусса для вектораD:

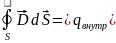
П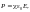 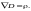оток вектора электрического смещения сквозь произвольную замкнутую поверхность равен алгебраической сумме сторонних (свободных) зарядов, охватываемых этой поверхностью. В дифференциальной форме: В случае изотропных диэлектриков, для которыхполучаем:

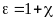
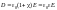
Величина

называется диэлектрической проницаемостьювещества.

Поле вектора D также может быть представлено с помощью линий, направление и густота которых определяются точно так же как и для линий вектора E. Источниками и стоками поляD являются только сторонние заряды.

12.Условия на границе раздела двух диэлектриков.

Р ассмотрим как ведут себя вектор электрического смещения и вектор напряженности электростатического поля на границе раздела двух сред. Для этого воспользуемся теоремой о циркуляции для вектора E и теоремой Гаусса для вектораD. Пусть поле вблизи границы разделаравно cоответственно

E1 и E2.Найдемциркуляцию вектора E

вдоль контура, имеющегоформу

вытянутого прямоугольника.

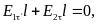
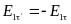
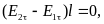
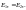
Т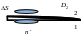 ангенциальная составляющая вектора E не

претерпевает скачок на границе раздела.Возьмем очень малой высоты цилиндр, расположив его на границе раздела, и воспользуемся теоремой Гаусса для вектора D.

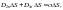
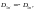
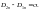
Е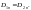 сли сторонние заряды на границе раздела отсутствуют,

Нормальная составляющая вектора D не

и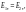 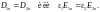спытывает скачок на границе раздела двух сред, если нет сторонних зарядов на границе.Рассмотрим полученные условия:

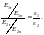
Р азделим одно на другое, получим

Рассмотрим рисунок:

Из рисунка:

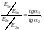
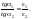
Следовательно:

Полученный закон преломления справедлив и для линий вектора электрического смещенияD.

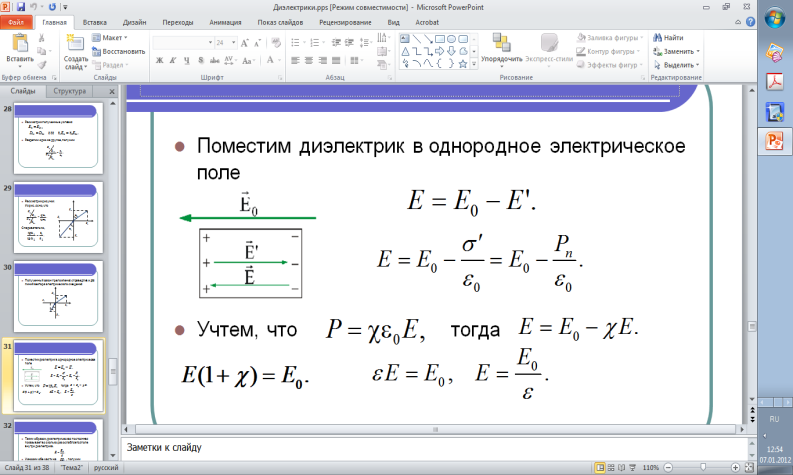
Т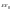 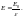аким образом, диэлектрическая постоянная показывает во сколько раз ослабляется поле внутри диэлектрика.

Умножим обе части на , получим