7.Силовые линии и эквипотенциальные поверхности. Свойства силовых линий.

С иловые линии – это линии, касательная к которым в любой точке поля совпадает с направлением вектора напряженности.В случае точечного заряда, линии напряженности исходят из положительного заряда и уходят в бесконечность; и из бесконеч­ности входят в отрицательный заряд. Густота силовых линий должна быть такой, чтобы единичную площадку, нормальную к вектору напряженности пересекало такое их число, которое равно либо пропорционально модулю вектора напряженности в данном месте. Связь напряженности поля с потенциалом позво­ляет доказать, что силовые линии всегда перпендикулярны к эквипотенциальным поверхностям и направлены в сторону убывания потенциала.Эквипотенциальная поверхность – это воображаемая поверхность, все точки которой имеют одинако­вый потенциал. Её уравнение:

С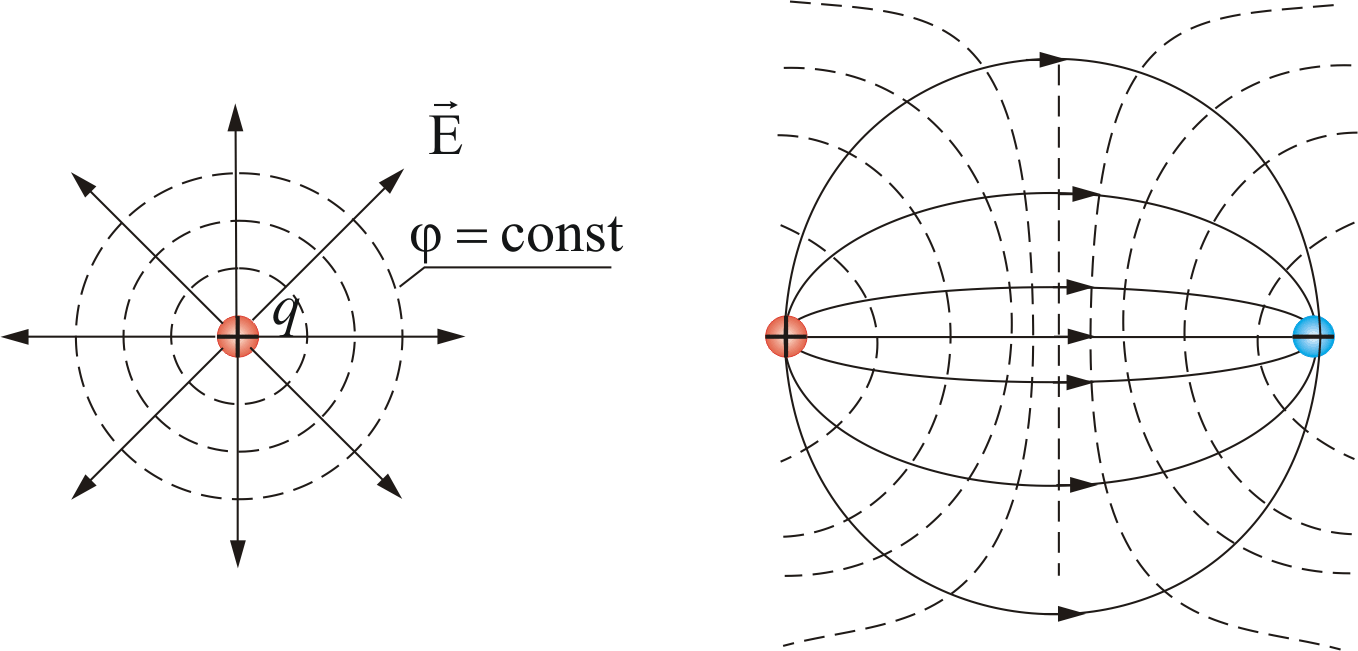 иловые линии и эквипотенциальные поверхности различных полей:

Силовые линии перпендикулярны к эквипотенциальным поверхностям.Эквипотенциальные поверхности проводят так, чтобы разность потенциалов для двух соседних поверхностей была бы одинаковой. По густоте эквипотенциальных поверхностей можно наглядно судить о значении напряженности поля в различных точках. Чем гуще расположены поверхности, тем напряженность поля больше.

8.Типы диэлектриков. Поляризованность.

Все известные в природе вещества, в соответствии с их способностью проводить электрический ток, делятся на три основных класса: проводники, полупроводники и диэлектрики.Диэлектрики – вещества, практически не проводящие электрического тока, так как в них отсутствуют свободные заряды, способные перемещаться на значительные расстояния.

Тем не менее при внесении диэлектрика в электрическое поле на его поверхности появляются электрические заряды, которые называются связанными.Смещение электрических зарядов вещества под действием электрического поля, в результате чего на поверхности, а также, вообще говоря, и в его объеме появляются нескомпенсированные заряды, называется поляризацией.Диэлектрики состоят либо из нейтральных молекул, либо из заряженных ионов, находящихся в узлах кристаллической решетки. Молекулы могут быть полярными и неполярными. У полярных молекул центр «тяжести» отрицательных зарядов сдвинут относительно центра «тяжести » положительных зарядов, в результате чего они обладают собственным дипольным моментом.Неполярные диэлектрики собственным дипольным моментом не обладают: у них центры «тяжести» положительного и отрицательного зарядов совпадают.Главное в поляризации – смещение зарядов в электростатическом поле. В результате, каждая молекула или атом приобретает дипольный момент.

9.Теорема Гаусса для вектора р.

Д ля количественного описания поляризации диэлектрика берут дипольный момент единицы объема.

где ΔV - физически бесконечно

м алый объем. Поляризованность можно

представить в виде

Д ля большинства диэлектриков:

Где - диэлектрическая восприимчивость, а β-поляризуемость одной молекулы.

Теорема Гаусса для вектора P:

Поток вектора P сквозь произвольную замкнутую поверхность S равен взятому с обратным знаком избыточному связанному заряду диэлектрика в объеме, охватываемом поверхностью S.