
- •4.Энергетическая характеристика поля - потенциал. Потенциал точечного заряда. Принцип суперпозиции потенциалов.
- •5.Теорема о циркуляции вектора e.
- •6.Связь между напряженностью поля и разностью потенциалов
- •7.Силовые линии и эквипотенциальные поверхности. Свойства силовых линий.
- •8.Типы диэлектриков. Поляризованность.
- •9.Теорема Гаусса для вектора р.
- •10.Поведение вектора р на границе раздела двух сред.
- •12.Условия на границе раздела двух диэлектриков.
- •13.Поле внутри проводника. Статический случай.
- •14.Электроемкость уединенного проводника и конденсатора. Плоский конденсатор.
- •15.Электроемкость сферического конденсатора
- •16.Электроемкость цилиндрического конденсатора
- •17.Энергия взаимодействия зарядов
- •1 8.Энергия электрического поля (уединенный проводник, конденсатор).
- •19.Характеристики и условия существования электрического тока.
- •20.Уравнение непрерывности.
- •21.Закон Ома и закон Джоуля-Ленца в дифференциальной форме.
- •22.Классическая теория электропроводности
- •25.Виток с током в магнитном поле.
- •26.Линии вектора магнитной индукции. Теорема Гаусса для вектора в.
- •27.Теорема о циркуляции вектора Вв интегральной и дифференциальной формах.
- •28.Магнитное поле движущегося заряда.
- •2 9.Сила Лоренца.
- •30.Движение заряженной частицы в магнитном поле
1 .Свойства
заряда. Закон Кулона. Электрическое
поле и его силовая характеристика.
Физическая
величина, определяющая способность
частиц участвовать в электрическом
взаимодействии, называется электрическим
зарядом этой
частицы. Электрический заряд – это
неотъемлемое свойство элементарной
частицы, и без нее сам по себе заряд
существовать не может. Свойства
электрических зарядов:
1.Существование
двух видов электрических зарядов
(«положительных»
и «отрицательных»),
отличающихся лишь тем, что все заряды
одного знака отталкиваются друг от
друга, а противоположные по знаку –
притягиваются. 2.Дискретность
величины электрического заряда. В
природе существует минимальный заряд,
называемый элементарным и равный по
величине 1,6*10^-19 Кл, а все заряды тел
кратны ему. 3.Аддиттивность.При
соединении нескольких заряженных тел
полный заряд оказывается равным
алгебраической сумме зарядов соединяемых
тел. 4.Сохранение
заряда.
Согласно закону сохранения заряда, в
изолированной системе полный заряд
всех тел остается неизменным при любых
взаимодействиях тел, приводящих к
перераспределению зарядов между ними.
5.Инвариантность.
Электрический заряд остается неизменным
при переходе от одной системы отсчета
к другой. Вокруг любого электрического
заряда (подвижного либо неподвижного)
создаётся электрическое поле, которое
проявляет себя в том, что на любой
пробный заряд, внесённый в это поле,
начинает действовать сила. Пробный
заряд –
такой заряд, который не вносит искажение
в исследуемое электрическое поле. Закон
Кулона. Взаимодействие заряженных тел
осуществляется посредством электрических
полей, образованных этими телами.
Взаимодействие точечных зарядов в
вакууме описывается законом Кулона:
.Свойства
заряда. Закон Кулона. Электрическое
поле и его силовая характеристика.
Физическая
величина, определяющая способность
частиц участвовать в электрическом
взаимодействии, называется электрическим
зарядом этой
частицы. Электрический заряд – это
неотъемлемое свойство элементарной
частицы, и без нее сам по себе заряд
существовать не может. Свойства
электрических зарядов:
1.Существование
двух видов электрических зарядов
(«положительных»
и «отрицательных»),
отличающихся лишь тем, что все заряды
одного знака отталкиваются друг от
друга, а противоположные по знаку –
притягиваются. 2.Дискретность
величины электрического заряда. В
природе существует минимальный заряд,
называемый элементарным и равный по
величине 1,6*10^-19 Кл, а все заряды тел
кратны ему. 3.Аддиттивность.При
соединении нескольких заряженных тел
полный заряд оказывается равным
алгебраической сумме зарядов соединяемых
тел. 4.Сохранение
заряда.
Согласно закону сохранения заряда, в
изолированной системе полный заряд
всех тел остается неизменным при любых
взаимодействиях тел, приводящих к
перераспределению зарядов между ними.
5.Инвариантность.
Электрический заряд остается неизменным
при переходе от одной системы отсчета
к другой. Вокруг любого электрического
заряда (подвижного либо неподвижного)
создаётся электрическое поле, которое
проявляет себя в том, что на любой
пробный заряд, внесённый в это поле,
начинает действовать сила. Пробный
заряд –
такой заряд, который не вносит искажение
в исследуемое электрическое поле. Закон
Кулона. Взаимодействие заряженных тел
осуществляется посредством электрических
полей, образованных этими телами.
Взаимодействие точечных зарядов в
вакууме описывается законом Кулона:
 Т
Т очечным
зарядом
называется заряженное тело, размеры
которого пренебрежительно малы по
сравнению с расстоянием до других
заряженных тел, с которым оно
взаимодействует. Таким образом, сила
взаимодействия точечных зарядов в
вакууме пропорциональна величине
зарядов и обратно пропорциональна
квадрату расстояния между ними. В
векторной форме закон Кулона записывается:
очечным
зарядом
называется заряженное тело, размеры
которого пренебрежительно малы по
сравнению с расстоянием до других
заряженных тел, с которым оно
взаимодействует. Таким образом, сила
взаимодействия точечных зарядов в
вакууме пропорциональна величине
зарядов и обратно пропорциональна
квадрату расстояния между ними. В
векторной форме закон Кулона записывается:
 г
г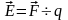 де
F12
- сила, действующая на заряд q1,
со стороны заряда q2.F21
– сила, действующая на за зарядq2
со сторонызарядаq1.(r2-r1)/(|r2-r1|)-
единичный вектор, направленный от
заряда q1
к заряду q2.Электрическим
полем
называется часть пространства, в которой
на помещенный туда электрический заряд
действуют электрические силы.Основное
свойство поля заключается в том, что
на всякий заряд, помещенный в это поле,
действует сила.Силовой
характеристикой
поля, создаваемого зарядом q,
является напряженность
электростатического поля, которая
определяется отношением силы, действующей
на заряд, к величине этого заряда.
де
F12
- сила, действующая на заряд q1,
со стороны заряда q2.F21
– сила, действующая на за зарядq2
со сторонызарядаq1.(r2-r1)/(|r2-r1|)-
единичный вектор, направленный от
заряда q1
к заряду q2.Электрическим
полем
называется часть пространства, в которой
на помещенный туда электрический заряд
действуют электрические силы.Основное
свойство поля заключается в том, что
на всякий заряд, помещенный в это поле,
действует сила.Силовой
характеристикой
поля, создаваемого зарядом q,
является напряженность
электростатического поля, которая
определяется отношением силы, действующей
на заряд, к величине этого заряда.
2 .
Напряженность поля точечного заряда
Принцип суперпозиции электрических
полей.Напряженность
поля, созданного точечным зарядом,
легко получается из закона Кулона:
.
Напряженность поля точечного заряда
Принцип суперпозиции электрических
полей.Напряженность
поля, созданного точечным зарядом,
легко получается из закона Кулона:
 Поля,
одновременно созданные во
однойи
той же областиразличными
ными
источниками, существуют неза
независимо
друг от друга.Напряженность поля,
созданного системой зарядов, определяется
в каждой точке пространства как
геометрическая сумма напряженностей
полей отдельных зарядов – принцип
суперпозиции полей.
Для дискретного распределения зарядов:
Поля,
одновременно созданные во
однойи
той же областиразличными
ными
источниками, существуют неза
независимо
друг от друга.Напряженность поля,
созданного системой зарядов, определяется
в каждой точке пространства как
геометрическая сумма напряженностей
полей отдельных зарядов – принцип
суперпозиции полей.
Для дискретного распределения зарядов:
Д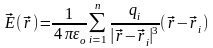 ля
системы точечных зарядов:
ля
системы точечных зарядов:
Когда заряд непрерывнораспределён в какой-либо области пространства, областипространства вводятся вводятсяпонятиялинейной плотности заряда (заряд единицы длины):
поверхностной плотности заряда (заряд единицы площади):
и объемной плотности заряда (заряд единицы
объёма):
объемной плотности заряда (заряд единицы
объёма):

 Соответственно
заряд элемента
Соответственно
заряд элемента
Длины dl, поверхности dS и
объёма dVравенλdl, σdS, ρdV.
А напряжённось рассчитывается по формулам:

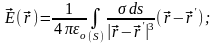
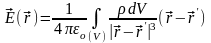
3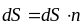
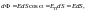 .Теорема
Гаусса для вектора Е в интегральной и
дифференциальной формах.Силовые линии
– это линии, касательная к которым в
любой точке поля совпадает с направлением
вектора напряженности.Однородным
называется электростатическое поле,
во всех точках которого напряженность
одинакова по величине и направлению.Полное
число силовых линий, проходящих через
поверхность S называется потоком вектора
напряженности Ф через эту поверхность.Так
как густота линий равна модулю вектора
напряженности поля, то поток
через элементарную площадкуможет
быть определен как:
.Теорема
Гаусса для вектора Е в интегральной и
дифференциальной формах.Силовые линии
– это линии, касательная к которым в
любой точке поля совпадает с направлением
вектора напряженности.Однородным
называется электростатическое поле,
во всех точках которого напряженность
одинакова по величине и направлению.Полное
число силовых линий, проходящих через
поверхность S называется потоком вектора
напряженности Ф через эту поверхность.Так
как густота линий равна модулю вектора
напряженности поля, то поток
через элементарную площадкуможет
быть определен как:
где
Т олько
в пределах элементарной площадкиdS
в общем случае вектор Eможно
считать постоянным. Для произвольной
поверхности поток
через нее определяется:
олько
в пределах элементарной площадкиdS
в общем случае вектор Eможно
считать постоянным. Для произвольной
поверхности поток
через нее определяется:
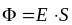
Для однородного поля:
Поток величина алгебраическая (скаляр), зависящая от выбора направления нормали (угла αмежду направлением нормали и вектором напряженности поля ). Может быть положителен, отрицателен, равен нулю. В случае замкнутой поверхности выбирают внешнюю нормаль.Теорема Остроградского-Гаусса:
Поток вектора напряженности сквозь замкнутую поверхность равен алгебраической сумме зарядов внутри этой поверхности, деленной на ε0.

С помощью теоремы Гаусса можно рассчитать напряжённость поля в случает симметричного распределения заряда по телу. Заряд может быть распределён по объёму, по поверхности и вдоль линии.
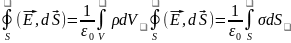

Дифференциальная форма (дивергенция):
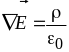
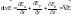
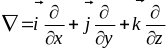
4.Энергетическая характеристика поля - потенциал. Потенциал точечного заряда. Принцип суперпозиции потенциалов.
С уществует
еще одна (помимо силовой-апряженность)характеристика
поля – энергетическая, названная
потенциалом.Потенциал
численно
равен потенциальной энергии, которой
обладает в данной точке поля единичный
положительный заряд.
уществует
еще одна (помимо силовой-апряженность)характеристика
поля – энергетическая, названная
потенциалом.Потенциал
численно
равен потенциальной энергии, которой
обладает в данной точке поля единичный
положительный заряд.
С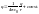 ледовательно
потенциал поля точечного заряда
ледовательно
потенциал поля точечного заряда
Равен:
Е сли
принять потенциал поля на бесконечном
удалении от заряда равным нулю, то можно
дать другое определение потенциала:
потенциал
численно равен работе, которую совершают
силы поля над единичным положительным
зарядом при удалении его из данной
точки в бесконечность
сли
принять потенциал поля на бесконечном
удалении от заряда равным нулю, то можно
дать другое определение потенциала:
потенциал
численно равен работе, которую совершают
силы поля над единичным положительным
зарядом при удалении его из данной
точки в бесконечность
Потенциал поля, создаваемый системой зарядов, в соответствии с принципом суперпозиции, равен алгебраической сумме потенциалов, создаваемых каждым из зарядов в отдельности.
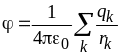
Для
непрерывного распределения зарядов: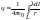
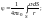

5.Теорема о циркуляции вектора e.
Интеграл
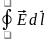 называют
циркуляцией. А утверждение
называют
циркуляцией. А утверждение


 теоремой
о циркуляции.
Циркуляция вектора напряжённости
электростатического поля по любому
замкнутому контуру равна нулю. Теорема
о циркуляции говорит о том, любое
электростатическое поле является
потенциальным. Теорема позволяет
сделать ряд важных выводов, практически
не прибегая к расчётам: линии
электростатического поля не могут быть
замкнутыми. Если это не так, и какая-то
линия – замкнута, то, взяв циркуляцию
вдоль этой линии, мы сразу же придем к
противоречию с теоремой о циркуляции
вектора E.
Интегрирование вдоль замкнутой силовой
линии даст результат отличный от
нуля.Величина
называетсяротором
(вихрем).
теоремой
о циркуляции.
Циркуляция вектора напряжённости
электростатического поля по любому
замкнутому контуру равна нулю. Теорема
о циркуляции говорит о том, любое
электростатическое поле является
потенциальным. Теорема позволяет
сделать ряд важных выводов, практически
не прибегая к расчётам: линии
электростатического поля не могут быть
замкнутыми. Если это не так, и какая-то
линия – замкнута, то, взяв циркуляцию
вдоль этой линии, мы сразу же придем к
противоречию с теоремой о циркуляции
вектора E.
Интегрирование вдоль замкнутой силовой
линии даст результат отличный от
нуля.Величина
называетсяротором
(вихрем).
В ажнейшее
уравнениеэлектростатики: ротор вектора
напряженностиэлектростатического
поля равен
нулю(электростатическое поле
безвихревое).Теорему
о циркуляции вектора напряженности
электростатического поля можно получить
также используя теорему Стокса:
ажнейшее
уравнениеэлектростатики: ротор вектора
напряженностиэлектростатического
поля равен
нулю(электростатическое поле
безвихревое).Теорему
о циркуляции вектора напряженности
электростатического поля можно получить
также используя теорему Стокса:
Эта теорема связывает контурный и поверхностный интегралы. Контур Lограничивает поверхность S, ориентация которой определяется направлением вектора положительной нормали. Направление обхода по контуру связано с направлением нормали к поверхности, ограниченной контуром правилом правого винта.
6.Связь между напряженностью поля и разностью потенциалов
Р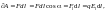 аботу,
совершенную силами электростатического
поля на бесконечно малом отрезке dl
можно найти так:
аботу,
совершенную силами электростатического
поля на бесконечно малом отрезке dl
можно найти так:
Э та
работа равна убыли потенциальной
энергии:
та
работа равна убыли потенциальной
энергии:
Приравнивая два выражения для работы, получаем:


Вспомним связь силы с
потенциальной
энергией:

Окончательно:
Фомулавыражает связь потенциала с напряженностью и позволяет по известным значениям φ найти напряженность поля в каждой точке.Можно решить и обратную задачу, т.е. по известным значениям E в каждой точке поля найти разность потенциалов между двумя произвольными точками поля:

