
- •30.Движение заряженной частицы в магнитном поле
- •31.Эффект Холла.
- •3 2.Явление электромагнитной индукции. Контур движется в магнитном поле.
- •33.Явление электромагнитной индукции. Контур неподвижен.
- •34.Явление самоиндукции. Ток размыкания
- •35.Явление самоиндукции Ток замыкания.
- •36.Взаимная индукция.
- •37.Магнитная энергия поля
- •38.Магнитная энергия двух контуров с токами.
- •39.Магнитное поле в веществе. Намагниченность. Токи намагничивания.
- •40.Напряженность магнитного поля Теорема о циркуляции вектора н.
- •4 1.Условия на границе раздела двух магнетиков.
- •42.Ток смещения.
- •46.Плоская электромагнитная волна. Вектор Умова-Пойтинга.
- •44.Уравнения Максвелла для стационарных полей и нейтральных непроводящих сред.
- •45.Электромагнитныеволны.
- •46.Плоская электромагнитная волна. Вектор Умова-Пойтинга.
- •47.Излучение диполя.
- •48.Интерференция света (два когерентных источника).
- •49.Интерференция в тонких пленках.
- •50.Многолучевая интерференция.
- •51.Дифракция света на круглом отверстии.
- •52.Дифракция света на круглом диске.
46.Плоская электромагнитная волна. Вектор Умова-Пойтинга.
В
 олновое
уравнение плоской электромагнитной
волны, распространяющейся вдоль оси
х имеет вид:
олновое
уравнение плоской электромагнитной
волны, распространяющейся вдоль оси
х имеет вид:
П
 ростейшим
решением этих уравнений являются
функции:
ростейшим
решением этих уравнений являются
функции:

Уравнение электромагнитной волны в векторной форме:


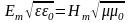

Причём:
44.Уравнения Максвелла для стационарных полей и нейтральных непроводящих сред.
Стационарные поля – поля постоянные во времени.




О![]()
![]() чем
говорят уравнения Максвелла? Электрическое
поле может возникнуть по двум причинам:
1. Его источником являются заряды как
сторонние, так и связанные
чем
говорят уравнения Максвелла? Электрическое
поле может возникнуть по двум причинам:
1. Его источником являются заряды как
сторонние, так и связанные
 ,
,
2. Переменное магнитное поле:
М агнитное
поле возбуждается либо движущимися
зарядами (токами), либо переменными
электрическими полями, либо и тем и
другим одновременно:
агнитное
поле возбуждается либо движущимися
зарядами (токами), либо переменными
электрическими полями, либо и тем и
другим одновременно:




У
 равнения
Максвелла в нейтральной непроводящей
среде:
равнения
Максвелла в нейтральной непроводящей
среде:
В нейтральной непроводящей среде, где
Уравнения Максвелла приобретают симметричный
в
 ид
с точностью до знака:
ид
с точностью до знака:


Л

 инии
вихревого электрического поля,
индуцированного изменениями поля
, образуют с вектором E-
левовинтовуюсистему,
в то время как линии магнитного поля,
индуцируемого изменением , образуют
с вектором H
правовинтовую систему.
инии
вихревого электрического поля,
индуцированного изменениями поля
, образуют с вектором E-
левовинтовуюсистему,
в то время как линии магнитного поля,
индуцируемого изменением , образуют
с вектором H
правовинтовую систему.
45.Электромагнитныеволны.
И
 з
уравнений Максвелла следует вывод о
существовании нового физического
явления - электромагнитное поле может
существовать самостоятельно – без
электрических зарядов и токов. При этом
изменение его состояния имеет волновой
характер. Поля такого рода называются
электромагнитными волнами. Рассмотрим
однородную нейтральную (ρ=0)
непроводящую среду (j=0)
с постояннымиε
и μ.
Запишем уравнения Максвелла и дополним
их материальными условиями.
з
уравнений Максвелла следует вывод о
существовании нового физического
явления - электромагнитное поле может
существовать самостоятельно – без
электрических зарядов и токов. При этом
изменение его состояния имеет волновой
характер. Поля такого рода называются
электромагнитными волнами. Рассмотрим
однородную нейтральную (ρ=0)
непроводящую среду (j=0)
с постояннымиε
и μ.
Запишем уравнения Максвелла и дополним
их материальными условиями.





 Произведем
подстановку материальных условий в
уравнения:
Произведем
подстановку материальных условий в
уравнения:


, , ,
В озьмем
ротор от обеих частей уравнений:
озьмем
ротор от обеих частей уравнений:
Р аскроем
ротор ротора:
аскроем
ротор ротора:

И используем: Получим



(1)
А налогичная
процедура для второго уравнения
приводит к результату:
налогичная
процедура для второго уравнения
приводит к результату:

(2) Учтём что
Уравнения (1) и (2)представляют собой типичные
волновые уравнения. Функция, удовлетворяющая такому уравнению, описывает волну, распространяющую с фазовой скоростью (3) .
46.Плоская электромагнитная волна. Вектор Умова-Пойтинга.
Э
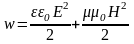 лектромагнитные
волны переносят энергию. Плотность
потока энергии можно получить, если
умножить плотность энергии на скорость
распространения волны. Плотность
энергии электромагнитной волны
так как
лектромагнитные
волны переносят энергию. Плотность
потока энергии можно получить, если
умножить плотность энергии на скорость
распространения волны. Плотность
энергии электромагнитной волны
так как

 то
то
что можно записать в виде

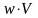

 Умножив ,
получим для плотности потока энергии
Умножив ,
получим для плотности потока энергии
Т.к. и образуют правовинтовую систему, то вектор
 совпадает
с направлением распространения волны
и
совпадает
с направлением распространения волны
и
р
 авен
по модулюСледовательно, вектор плотности
потока энергии
авен
по модулюСледовательно, вектор плотности
потока энергии


 Вектор
называется вектором
Пойтинга.
Поток электромагнитной энергии
через произвольную поверхность
можно найти как
Вектор
называется вектором
Пойтинга.
Поток электромагнитной энергии
через произвольную поверхность
можно найти как
