
- •30.Движение заряженной частицы в магнитном поле
- •31.Эффект Холла.
- •3 2.Явление электромагнитной индукции. Контур движется в магнитном поле.
- •33.Явление электромагнитной индукции. Контур неподвижен.
- •34.Явление самоиндукции. Ток размыкания
- •35.Явление самоиндукции Ток замыкания.
- •36.Взаимная индукция.
- •37.Магнитная энергия поля
- •38.Магнитная энергия двух контуров с токами.
- •39.Магнитное поле в веществе. Намагниченность. Токи намагничивания.
- •40.Напряженность магнитного поля Теорема о циркуляции вектора н.
- •4 1.Условия на границе раздела двух магнетиков.
- •42.Ток смещения.
- •46.Плоская электромагнитная волна. Вектор Умова-Пойтинга.
- •44.Уравнения Максвелла для стационарных полей и нейтральных непроводящих сред.
- •45.Электромагнитныеволны.
- •46.Плоская электромагнитная волна. Вектор Умова-Пойтинга.
- •47.Излучение диполя.
- •48.Интерференция света (два когерентных источника).
- •49.Интерференция в тонких пленках.
- •50.Многолучевая интерференция.
- •51.Дифракция света на круглом отверстии.
- •52.Дифракция света на круглом диске.
40.Напряженность магнитного поля Теорема о циркуляции вектора н.
В магнетиках, помещенных в магнитное
поле , возникают токи намагничивания,
поэтому циркуляция вектора Bтеперь
будет определяться не только токами
проводимости, но и токами намагничивания:
Воспользуемся
магнетиках, помещенных в магнитное
поле , возникают токи намагничивания,
поэтому циркуляция вектора Bтеперь
будет определяться не только токами
проводимости, но и токами намагничивания:
Воспользуемся

теоремой о циркуляции вектора J.
Ц
 иркуляции
берутся по одному контуру, тогда:
иркуляции
берутся по одному контуру, тогда:
Или
В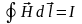
 еличину,
стоящую под интегралом, обозначим
буквой H
- вспомогательный вектор, получивший
название напряженности магнитного
поля:
еличину,
стоящую под интегралом, обозначим
буквой H
- вспомогательный вектор, получивший
название напряженности магнитного
поля:
Следовательно
Ц иркуляция
вектора Hпо
произвольному замкнутому контуру равна
алгебраической сумме токов проводимости,
охватываемых этим контуром (теорема о
циркуляции вектора H).
Правило знаков такое же как и для
циркуляции вектора B.
В дифференциальной форме:
Ротор вектора H
равен плотности тока
тока
проводимости.
иркуляция
вектора Hпо
произвольному замкнутому контуру равна
алгебраической сумме токов проводимости,
охватываемых этим контуром (теорема о
циркуляции вектора H).
Правило знаков такое же как и для
циркуляции вектора B.
В дифференциальной форме:
Ротор вектора H
равен плотности тока
тока
проводимости.
4 1.Условия на границе раздела двух магнетиков.
П
 олучим
условия с помощью теоремы Гаусса
олучим
условия с помощью теоремы Гаусса
и теоремы о циркуляции.
Представим малой высоты цилиндрик,
расположенный на границе раздела
магнетиков. Тогда поток вектора B
через основания ΔS(потоком через
боковую поверхность пренебрегаем)
м ожно
записать:
ожно
записать:
В
 зяв
проекции на общую нормаль, получим:
зяв
проекции на общую нормаль, получим:
Т.е.
н ормальная
составляющая вектора B
на границе двух сред скачка не испытывает.
Далее предположим, что вдоль границы
ормальная
составляющая вектора B
на границе двух сред скачка не испытывает.
Далее предположим, что вдоль границы
раздела течет поверхностный ток
проводимости с линейной
плотностью i. Применим
теорему о циркуляции
вектора H к очень малому
прямоугольному контуру, высота
которого пренебрежимо мала по сравнению с его длиной.
П
 ренебрегая
вкладом в циркуляцию на боковых сторонах
контура, получим:
ренебрегая
вкладом в циркуляцию на боковых сторонах
контура, получим:
где -
п роекция
плотности тока проводимости на нормаль
к контуру.
роекция
плотности тока проводимости на нормаль
к контуру.
В
 зяв
проекции на общий орт касательной
:
зяв
проекции на общий орт касательной
:
П олучим
олучим
Е


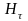

 сли
на границе раздела магнетиков токов
проводимости нет
, то:Таким образом, если на границе
раздела двух
однородных магнетиков токов проводи-мости
нет, то составляющие и
изменяются непрерывно, без скачка, а
составляющие и претерпевают
скачок. В результате на границе раздела
двух магнетиков линии вектора B
(вектора H)
испытываютпре-ломление, причем
сли
на границе раздела магнетиков токов
проводимости нет
, то:Таким образом, если на границе
раздела двух
однородных магнетиков токов проводи-мости
нет, то составляющие и
изменяются непрерывно, без скачка, а
составляющие и претерпевают
скачок. В результате на границе раздела
двух магнетиков линии вектора B
(вектора H)
испытываютпре-ломление, причем
42.Ток смещения.
Ф
 арадей
доказал, что изменяющееся во времени
магнитное поле создает электрическое
поле.Максвелл высказал мысль, что
электрическое поле, меняющееся во
времени, должно создавать магнитное
поле.К этой идее можно придти с помощью
следующих рассуждений.Рассмотрим
участок цепи, содержащей конденсатор,
разряжающийся через внешнее
сопротивление.Согласно теореме о
циркуляции
арадей
доказал, что изменяющееся во времени
магнитное поле создает электрическое
поле.Максвелл высказал мысль, что
электрическое поле, меняющееся во
времени, должно создавать магнитное
поле.К этой идее можно придти с помощью
следующих рассуждений.Рассмотрим
участок цепи, содержащей конденсатор,
разряжающийся через внешнее
сопротивление.Согласно теореме о
циркуляции
(1)
В качестве контура возьмем
контур, охватывающий ток. На этот контур можно натянуть две
совершенно равноправные поверхностиS1 и S2.
Р
 ассмотрим
циркуляцию вектора H
по произвольному контуру. (1) Для
поверхности S1:
ассмотрим
циркуляцию вектора H
по произвольному контуру. (1) Для
поверхности S1:
Для S2:
Циркуляция вектора H не может зависеть от выбора поверхности.Проведем следующие рассуждения.Заметим, что поверхность S1 пронизывает только
э лектрическое
поле. Воспользуемся теоремой Гаусса
для вектора D:
лектрическое
поле. Воспользуемся теоремой Гаусса
для вектора D:
Продифференцируем по времени и
поменяем порядок действий:
В

 оспользуемся
ура-ем непрерывности:
оспользуемся
ура-ем непрерывности:
Сложим уравнения:
Полученное уравнение аналогично
У равнению
непрерывности для по-
равнению
непрерывности для по-
стоянного тока, в котором кроме плотности тока имеется слагаемое той же размерности:
Максвелл назвал это слагаемое плотностью тока смещения.
С умму
тока смещения и тока проводимости
называют п
полным током. Его плотность равна
умму
тока смещения и тока проводимости
называют п
полным током. Его плотность равна
Токи смещения существуют лишь там, где
меняется со временем электрическое поле.
4
 3.Уравнения
Максвелла и их свойства. Система
уравнений
3.Уравнения
Максвелла и их свойства. Система
уравнений
1) 2)


3) 4)
1![]() )Циркуляциявектора
E
по любому замкнутому контуру равна
взятой со знаком минус производной по
времени от магнитного потока через
любую поверхность, ограниченную данным
контуром.2)Поток
вектора D
сквозь любую замкнутую поверхность
равен алгебраической сумме сторонних
зарядов, охватываемых этой поверхностью.
3)Циркуляция
вектора H
по любому замкнутому контуру равна
полному току через произвольную
поверхность, ограниченную данным
контуром. 4)Поток
вектора B
сквозь произвольную замкнутую поверхность
всегда равен нулю. Система уравнений
Максвелла в дифференциальной форме:
)Циркуляциявектора
E
по любому замкнутому контуру равна
взятой со знаком минус производной по
времени от магнитного потока через
любую поверхность, ограниченную данным
контуром.2)Поток
вектора D
сквозь любую замкнутую поверхность
равен алгебраической сумме сторонних
зарядов, охватываемых этой поверхностью.
3)Циркуляция
вектора H
по любому замкнутому контуру равна
полному току через произвольную
поверхность, ограниченную данным
контуром. 4)Поток
вектора B
сквозь произвольную замкнутую поверхность
всегда равен нулю. Система уравнений
Максвелла в дифференциальной форме:
![]()
![]()
![]()
У равнения
Максвелла совместно с уравнением
движения заряженных частиц под действием
силы Лоренца составляют фундаментальную
систему уравнений. Этой системы
достаточно для описания всех
электромагнитных явлений, в которых
не проявляются квантовые эффекты.
Чтобы найти поля по заданным
равнения
Максвелла совместно с уравнением
движения заряженных частиц под действием
силы Лоренца составляют фундаментальную
систему уравнений. Этой системы
достаточно для описания всех
электромагнитных явлений, в которых
не проявляются квантовые эффекты.
Чтобы найти поля по заданным
р аспределениям
зарядов и токов, необходимо уравнения
Максвелла дополнить материальными
уравнениями. В случае изотропных сред
без сегнетоэлектриков и ферромагнетиков
эти уравнения имеют вид:
аспределениям
зарядов и токов, необходимо уравнения
Максвелла дополнить материальными
уравнениями. В случае изотропных сред
без сегнетоэлектриков и ферромагнетиков
эти уравнения имеют вид:


Свойства уравнений Максвелла:
1)Уравнения Максвелла линейны. Содержат только первые производные полей E и B по времени и пространственным координатам и первые степени плотности электрических зарядов ρ и j токов. Свойство линейности непосредственно связано с принципом суперпозиции. 2)Уравнения Максвелла содержат уравнение непрерывности, выражающее закон сохранения электрического заряда.3)Уравнения Максвелла выполняются во всех инерциальных системах отсчета – они релятивистски инвариантны. 4)Уравнения Максвелла не симметричны относительно электрического и магнитного полей. Это обусловлено тем, что в природе не существует магнитных зарядов.
