18. Нахождение коэффициентов тригонометрического ряда по формулам Фурье.

Если n и k – целые числа, то

.

Отметим следующее свойство периодической функции ψ(х) с периодом 2π:

каково бы ни было число λ.

Указанное свойство означает, что интеграл от периодической функции ψ(х) по любому отрезку, длина которого равна периоду, имеет всегда одно и то же значение.

15. Разложение по степеням х функций ех, shx, chx, cosx, sinx.

1.

2.

3.

4.

f(0)=0

5.

.

Разложение по степеням X функций: и (разложение вывести для одной функции)

1) ;

;

;

при X=1 ряд тоже сходится

2) ; .

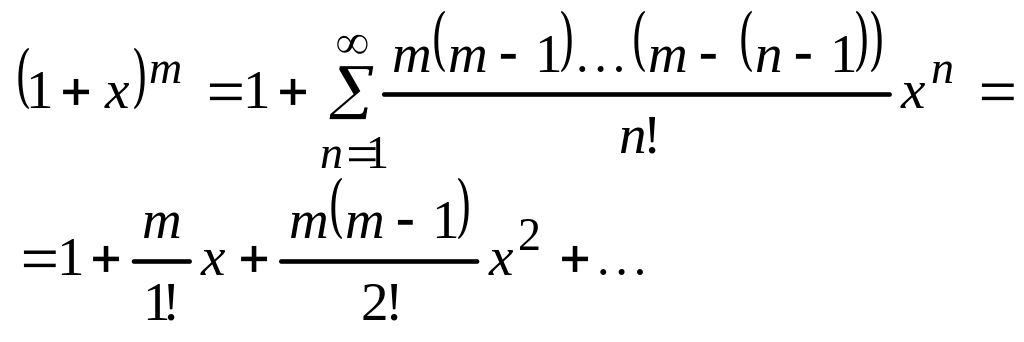16. Приложения степенных рядов. Приближенное вычисление значений ф-ций. Вычисление сумм числовых рядов.

Приближенное вычисление значений ф-ций.

- входит в обл. сходимости.

Подставляют

В зависимости от того, с какой точностью требуется вычислить оставляют достаточное число членов этого числового ряда. Достаточное число слагаемых берут из оценки достаточного члена ф-лы Тейлора или ост члена ряда Тейлора. Либо для знакочередуюшегося ряда, используя следствие из признака Лейбница.

Пример: Найти значение с точностью до 0,01

2) Вычисление сумм числовых рядов.

19. Разложение в ряд Фурье четных и нечетных ф-ций на интервале .

1. Пусть ф-ция f(x) – четная, т. е. f(-x)=f(x).

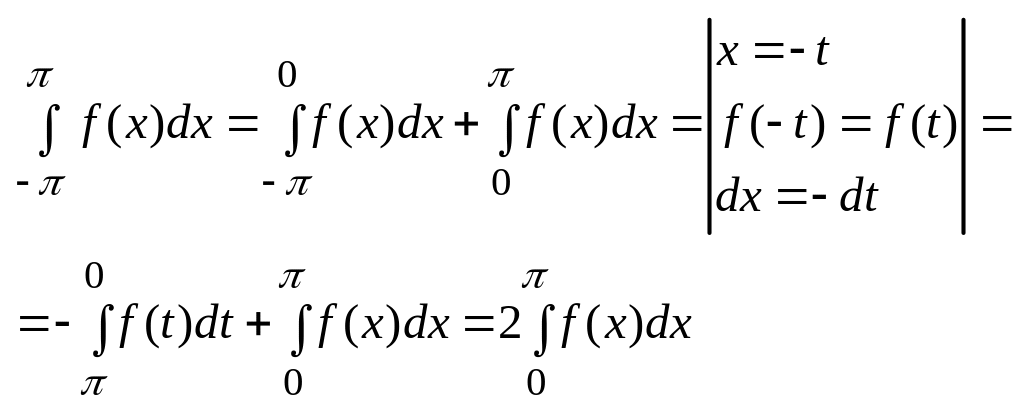
Значит:

;

;

.

Ряд Фурье для четных ф-ций – ряд только по косинусам

2. Пусть ф-ция f(x) – нечетная, т. е. f(-x)=-f(x).

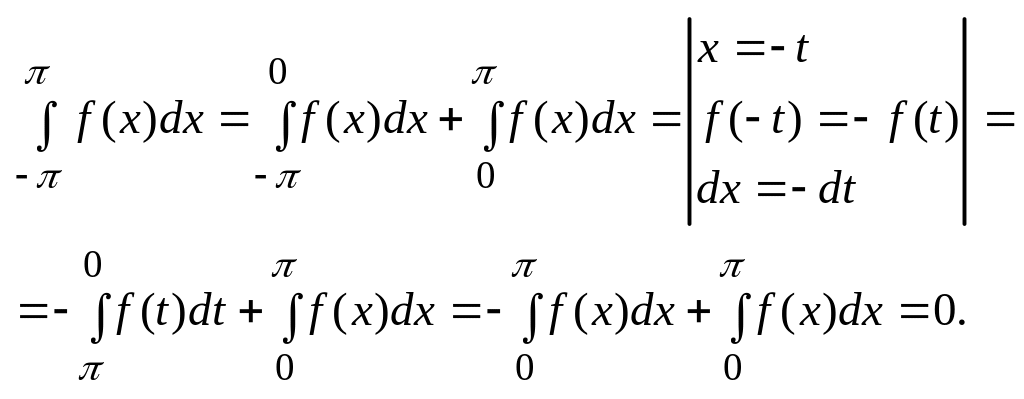
Значит:

;

;

.

Ряд Фурье для четных ф-ций – ряд только по синусам

20. Разложение в ряд Фурье функций, заданных на интервале [-l; l].

Пусть f(х) есть периодическая функция с периодом 2l, вообще говоря, отличным от 2π. Разложим ее в ряд Фурье.

Сделаем замену переменной по формуле: .

Тогда функция будет периодической функцией от t с периодом 2π. Ее можно разложить в ряд Фурье на отрезке :

где

Возвратимся теперь к старой переменной х:

Тогда будем иметь:

23.Интеграл Фурье.

Пусть ф-ция f(x) представлена на отрезке (-l;l)

, где

; ;

f(x) абсолютно интегрируема на , тогда * Ф-ция , стоящая в правой части явл. Ф-цией от переменных . Устремим . Можно показать что если ф-ция f(x) кусочно-монотонная и ограничена, то тогда превращается в следующее (при ) -интеграл Фурье.