
- •Гоу спо Калининградской области «Озёрский техникум природообустройства»
- •Н.С. Безрукова
- •Математика
- •Методические указания и контрольные задания для студентов заочной формы обучения
- •Для специальности
- •110301 «Механизация сельского хозяйства»
- •Общие методические указания
- •Требования к выполнению и оформлению контрольной работы.
- •Контрольная работа
- •Контрольная работа
- •Рекомендуемая литература
- •Содержание
- •110301 «Механизация сельского хозяйства»
Требования к выполнению и оформлению контрольной работы.
Каждая контрольная работа выполняется в отдельной тетради школьного формата в клетку. Следует пронумеровать страницы и оставить на них поля не менее 3 см для замечаний преподавателя.
На обложке тетради должен быть приклеен титульный лист утвержденного образца или аккуратно записаны все данные титульного листа: шифр, специальность, если она не отражена в шифре, фамилия, имя, отчество учащегося, предмет и номер работы.
Работу выполняют чернилами одного цвета , аккуратно, разборчиво.
Каждую задачу надо начинать с новой страницы.
Решения задач желательно располагать в порядке номеров , указанных в задании, номера задач следует указывать перед условием.
Условия задач необходимо переписывать полностью в контрольную тетрадь; к геометрическим задачам, кроме того, дается установленная краткая запись условия.
Чертежи следует выполнять карандашом с использованием чертежных инструментов , аккуратно , соблюдая масштаб.
При оформлении записей в тетради необходимо выполнять общие требования к культуре их ведения. Перечислим важнейшие из этих требований:
а) учащиеся должны соблюдать абзацы, всякую новую мысль следует начинать с красной строки;
б) важные формулы, равенства, определения нужно выделять в отдельные строки, чтобы сделать их более обозримыми;
в) при описании решения задачи краткая запись условия отделяется от решения и в конце решения ставится ответ;
г) серьезное внимание следует уделять правильному написанию сокращенных единиц величин;
д) необходимо правильно употреблять математические символы.
Решения задач должны сопровождаться краткими , но обоснованными пояснениями , используемые формулы нужно выписывать.
В конце работы следует указать список литературы , которой вы пользовались, проставить дату выполнения работы и подпись.
Если в работе допущены недочеты и ошибки, то учащийся должен выполнить все указания преподавателя, сделанные в рецензии.
Контрольная работа должна быть выполнена в срок в соответствии с учебным планом-графиком. В период сессии работы на проверку не принимаются.
Работа, выполненная не по своему варианту , не учитывается и возвращается студенту без рецензии и оценки.
Учащиеся, не имеющие зачета по контрольной работе, к экзамену не допускаются.
Во время экзамена зачтенные контрольные работы представляются преподавателю.
Критерии оценки контрольной работы
Оценка «Отлично» ставится, если все задания выполнены правильно и без ошибок.
Оценка «Хорошо» ставится, если выполнено 70% заданий полностью, и 10% с небольшими неточностями.
Оценка «Удовлетворительно» ставится, если выполнено полностью 50% заданий.
Оценка «Неудовлетворительно» ставится, если решено меньше 50% заданий.
Контрольная работа
Контрольная работа содержит задания, номера которых указаны в таблице распределения заданий по вариантам. Работу выполняют по букве, с которой начинается фамилия студента.
Задания контрольной работы
Задания 1-20
Движение тела но плоскости задано функцией y=f(x). Изучить траекторию движения тела, то есть:
Исследовать функцию y=f(x) . 2. Построить график функции y=f(x).
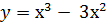 11.
у =
11.
у = 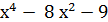
у =
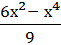 12. у =
12. у = 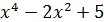
у =
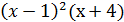 13. у =
13. у = 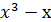
у =
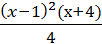 14.
у =
14.
у = 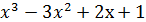
у =
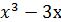 15. у =
15. у = 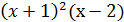
у =
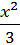 +х2
16. у =
+х2
16. у = 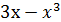
у = 12х – х3 17.
 х3 – х2 +
х3 – х2 + 
у =
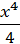 - 2
- 2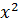 18. у =
18. у =  +2
+2у =
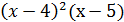 19. у =
19. у =  х3 – 4
х3 – 4
у = х3 – 4х2 – 3х+6 20. у = -2х2+4х.
Задания 21-25
Найти производные функций при заданном значении аргумента.
21. а) х2 - ![]() ; у1 = (2), у1(-2) б) у =
; у1 = (2), у1(-2) б) у = ![]() ; у1 = (0), у1(2)
; у1 = (0), у1(2)
22. а) у = ![]() ; у1(0) б) у =
; у1(0) б) у = ![]() ; у1 = (2), у1(е2)
; у1 = (2), у1(е2)
23. а) у = х![]() ;
у1 = (1), у1(е) б) у =
;
у1 = (1), у1(е) б) у =
![]() у1 = (0), у1(-1)
у1 = (0), у1(-1)
24. а) у = (х-1)(х3+2);
у1 = (0), у1 (2 б) у = ![]() х3- х; у1 = (0), у1(2),
х3- х; у1 = (0), у1(2),
25. а) у = (х – 1)(х3
+ 2); у1 = (1), у1 (2), б) у = ![]() ;
у1 = (0),
;
у1 = (0),
Задания 26 – 30
Найдите производные сложных функций.
26. а) у = ![]() б) у =
б) у = ![]()
27. а) у =![]() б) у = 2
б) у = 2![]()
28. а) у = ![]() б) у = tg(x2+
3)
б) у = tg(x2+
3)
29. а) у = sin2x3 б) у = lntg5x
30. а) у = lnsinx б) у = tg3x – 3tgx + 3x
Задания 31- 40
В следующих уравнениях найти:
общее решение дифференциальных уравнений;
частные решения уравнения по начальным условиям.
31. х у1 – у = 0 у0 = 4 при х0 = -2
32. у у1 + х = 0 у0 = 4 при х0 = -2
33. х2 у1 + у2 = 0 у0 = 1 при х0 = -1
34. х у1 + у = 0 у0 = 4 при х0 = -2
35. у1 = у у0 = 4 при х0 = -2
36. 2 у1![]() = у у0 = 1 при х0 = 4
= у у0 = 1 при х0 = 4
37. (2х + 1)dy + y2dx у0 = 1 при х0 = 4
38. (1 + ![]() )y
у1 = ex у0
= 1 при х0 = 0
)y
у1 = ex у0
= 1 при х0 = 0
39. 2![]() dx
= dy у0
= 1 при х0 = 0
dx
= dy у0
= 1 при х0 = 0
40. x
у1 = ![]() у0 = 1 при х0
= e
у0 = 1 при х0
= e
Задания 41 - 50
Найти общее решение:
а) линейных дифференциальных уравнений;
б) линейных однородных дифференциальных уравнений второго порядка
41. а) у1 – у ех б) у11 - 5 у1 + 4у = 0
42. а) у1 = х + у б) у11 - 6 у1 + 9у = 0
43. а) ху1 + у = ех б) у11 + 8 у1 +25у = 0
44. а) ху1 2у = х2 б) у11 - 3 у1 + 2у = 0
45. а) у1 = х + у б) у11 - 4 у1 + 4у = 0
46. у1 – ![]() б) у11 - 2 у1
+ 2у = 0
б) у11 - 2 у1
+ 2у = 0
47. у1![]() =
= ![]() б) у11 - 4 у1 + 3у = 0
б) у11 - 4 у1 + 3у = 0
48. а) у1 – ytgx = ctgx б) у11 + y = 0
49. а) ху1 + y = ln x + 1 б) у11 + 2 у1 + 5y = 0
50. а) ху1 + y = 3 б) у11 + 4 у1 = 0
Задания 51- 60
а) разложить в ряд Маклорена и найти интегралы сходимости функций;
б) исследовать ряд на сходимость по признаку Даламбера.
51. а) у = х2е-2х б)
![]()
52. а) у = ![]() б)
б) ![]()
53. а) y
= ![]() б)
б) ![]()
54. а) у = sin2x б)
![]()
55. а) у = sin
x2 б) ![]()
56. а) у = ![]() б)
б) ![]()
57. а) у = ![]() б)
б) ![]()
58. а) у = ![]() б)
б) ![]()
59. а) у = sin x2 б)
60. а) у = ln(1
+ 5x) б) ![]()
Задания 61- 70
Всхожесть семян
есть случайная величина. Исследования
всхожести семян методом выборки
представлены таблицей, в которой Х ![]() - характеристики случайной величины, N
- характеристики случайной величины, N
![]() - частота появления характеристик
выборки. Провести исследование выборки:
- частота появления характеристик
выборки. Провести исследование выборки:
а) найти объем выборки;
б) составить закон распределения случайной величины Х;
в) найти выборную среднюю дисперсию и среднее квадратичное отклонение.
61.
-
Х
2
4
9
N
10
20
30
62.
-
X
1
5
8
N
8
16
40
63.
-
X
4
7
10
N
10
5
15
64.
-
X
6
10
20
N
20
10
30
65.
-
X
2
4
5
N
8
7
6
66.
-
X
1
3
7
N
8
10
6
67.
-
X
3
8
10
N
20
10
15
68.
-
X
2
6
7
N
8
12
10
69.
-
X
1
4
7
N
20
15
10
70.
-
X
1
5
7
N
3
8
4
Задания 71- 80
Решить задачи теории вероятностей.
71. В ящике 30 яблок: 10 красных, 15 желтых и 5 незрелых. Наудачу извлекается яблоко. Найти вероятность извлечения зрелого (красного или желтого) яблока.
72. Ветеринарный участок получает пакеты с контрольными пробами из хозяйств А, В и С. Вероятность получения пакета из хозяйства А –
0,7, из хозяйства В – 0,2. Найти вероятность того, что очередной пакет будет получен из хозяйства С.
73. У сборщика имеется 3 конусных и 7 эллиптических валиков. Сборщик взял один валик, а затем второй. Найти вероятность того, что первый из взятых валиков – конусный, а второй – эллиптический.
74. Из слова «пчеловодство» выбирается наугад одна буква. Какова вероятность того, что это будет буква «о».
75. Имеется три ящика, содержащих 10 радиоламп. В первом ящике – 8, во втором – 7, в третьем – 9 стандартных радиоламп. Найти вероятность того, что все три вынутые лампы окажутся стандартными.
76. Исследуются две группы откормочного поголовья свиней: первая – 10 голов (из них 8 с высокими привесами), вторая – 15 голов (из них 12 с высокими привесами). Из каждой группы наудачу взяты по одному животному. Найти вероятность того, что оба животных окажутся с высокими привесами.
77. Три работника участвуют в стрижке овец. Вероятность выполнения работы без брака первого работника 0,75, второго – 0,8, третьего – 0,9. Найти вероятность того, что все три работника выполнят работу без брака.
78. Вероятность выхода из строя в течение одного рабочего дня равна 0,01. Какова вероятность того, что за 5 дней станок ни разу не выйдет из строя.
79. Среди 50 электроламп – 4 бракованных. Какова вероятность того, что две взятые наугад электролампы окажутся бракованными?
80. В ремонтной мастерской 14 слесарей и 16 токарей. Нужно выбрать делегацию из двух человек. Какова вероятность того, что выберут двух токарей?
Задания 81- 90
Опытный участок
представлен криволинейной трапецией,
ограниченной параллельными сторонами
и верхним основанием в виде ломаной
линии, выраженной функцией y = f(x), (a ![]()
Определить площадь опытного участка способами:
а) приближенного вычисления (прямоугольника, трапеции при n = 10,
б) точных расчетов (по формуле Ньютона – Лейбница).
Вычислить погрешности в расчетах:
а) абсолютную,
б) относительную.
№ |
f(x) |
способ |
|
|||
81 |
I = |
трапеции |
|
|||
82 |
I = |
прямоугольника |
|
|||
83 |
I= |
трапеции |
|
|||
84 |
I= |
трапеции |
|
|||
85 |
I= |
прямоугольника |
|
|||
|
|
|
|
|||
86 |
I = |
трапеции |
|
|||
87 |
I = |
прямоугольника |
|
|||
88 |
I = |
трапеции |
|
|||
89 |
I = |
трапеции |
|
|||
90 |
I = |
прямоугольника |
|
|||
|
|
|
|
|
|
|
Задания 91- 99.
Найти значение функции (четыре значения, определяемое дифференциальным уравнением у1 = f(x, y) при начальном условии у(0), с шагом h, используя метод Эйлера.
91. у1 = ![]() у(0) = 1; h = 0,1
у(0) = 1; h = 0,1
92. у1 = х + у у(0) = 1; h = 0,1
93. у1 = 1 + х + у2 у(0) = 1; h = 0,1
94. у1 = х2 + у2 у(0) = 0; h = 0,1
95. у1 = у2
+ ![]() у(0) = 4; h = 0,1
у(0) = 4; h = 0,1
96. у1 = у2 + х у(0) = 1; h = 0,1
97. у1 = у + 1 у(0) = 1; h = 0,2
98. у1 = у –
![]() у(0) = 1; h = 0,2
у(0) = 1; h = 0,2
99. у1 = ![]() + 0,5у у(0) = 1; h = 0,1
+ 0,5у у(0) = 1; h = 0,1
ПРИЛОЖЕНИЕ 1
ОБРАЗЕЦ ТИТУЛЬНОГО ЛИСТА (для заочной формы обучения)
Государственное образовательное учреждение
среднего профессионального образования Калининградской области
«Озерский техникум природообустройства»
