
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФГБОУ ВПО «Госуниверситет – УНПК»
Кафедра «Динамика и прочность машин»
Курсовая работа
по дисциплине «Техническая диагностика»
Работу выполнил студент Димов А.А.______________________
Специальность «Динамика и прочность машин» Группа 41-ДП
Руководитель Климов А.В._______________________________
Орел 2011
АННОТАЦИЯ
Данная курсовая работа посвящена задачам определения показателей надежности применительно к автомобильному транспорту. Эти показатели являются одним из важнейших условий, определяющих устойчивую работу транспортных систем.
В курсовой работе основное внимание уделено практическому определению критериев работоспособности основных узлов двигателей автомобилей, в частности, топливных форсунок, коленчатых валов, электронных блоков управления ДВС.
СОДЕРЖАНИЕ
Введение 4
Глава 1 5
Глава 2 6
Глава 3 7
Глава 4 9
Глава 5 9
Глава 6 10
Вывод 12
Список использованных источников 15
Введение
Техническая диагностика — молодая наука, возникшая в последние два десятилетия в связи с потребностями современной техники. Все возрастающее значение сложных и дорогостоящих технических систем, особенно в машиностроении и радиоэлектронике, требования безопасности, безотказности и долговечности делают весьма важной оценку состояния системы, ее надежности. Техническая диагностика — наука о распознавании состояния технической системы, включающая широкий круг проблем, связанных с получением и оценкой диагностической информации. Книга посвящена главным образом теоретическим основам технической диагностики. Изучение общих методов распознавания и математической теории диагностики дает возможность более обоснованного выбора конкретных способов диагностики и соответствующих им правил решения. При изложении теории диагностики особых требований к математической подготовке инженеров не предъявляется, хотя некоторые моменты могут показаться трудными при первоначальном ознакомлении. Математизация инженерных знаний является неизбежным процессом, связанным с развитием техники, однако следует всегда помнить, что цель расчета не число, а понимание.
Глава 1
Дано:![]() ч,
ч,
![]() ч.
ч.
Требуется:
определить статистические вероятности
безотказной работы
![]() и отказа
и отказа
![]() устройства для заданного значения
устройства для заданного значения
![]() .
Рассчитать значения вероятности
безотказной работы
.
Рассчитать значения вероятности
безотказной работы
![]() по первым 20 значениям наработки до
отказа. Для заданной наработки
рассчитать мат. ожидание числа
работоспособных устройств
по первым 20 значениям наработки до
отказа. Для заданной наработки
рассчитать мат. ожидание числа
работоспособных устройств
![]() .
.
Решение:
Статистическая вероятность безотказной работы устройства для наработки t определяется как:
![]() ,
,
где
![]() - число объектов, работоспособных на
момент времени t.
По условию
- число объектов, работоспособных на
момент времени t.
По условию
![]() ,
,
![]() .
Следовательно
.
Следовательно
![]() .
.
Вероятность отказа устройства за наработку t статистически определяется как
![]() ,
,
где
![]() - число объектов, неработоспособных к
наработке t.
Т.к.
- число объектов, неработоспособных к
наработке t.
Т.к.
![]() и
,
имеем:
и
,
имеем:
![]() .
.
Поскольку
![]() ,
нетрудно видеть, чему равна сумма
вероятностей
,
нетрудно видеть, чему равна сумма
вероятностей
![]() .
Из ранее сделанных вычислений имеем:
.
Из ранее сделанных вычислений имеем:
![]() ,
,
что подтверждает правильность вычислений.
Оценку вероятности
безотказной работы устройства по первым
20-ти значениям наработки до отказа
обозначим как
.
Ее значение определяется также по
формуле (1) но при этом
![]() ,
и число работоспособных объектов
выбирается из этой совокупности:
,
и число работоспособных объектов
выбирается из этой совокупности:
![]() .
.
Будем считать, что
условия опыта, включающего себя 50
наблюдений, позволили однозначно
определить вероятность безотказной
работы устройства, т. е.
![]() .
Здесь
.
Здесь
![]() - функция распределения случайной
величины «наработка до отказа»,
определяющая вероятность события
- функция распределения случайной
величины «наработка до отказа»,
определяющая вероятность события
![]() при
при
![]() .
.
Тогда с учетом формулы (1) математическое ожидание числа объектов , работоспособных к наработке t, определяется как:
![]() ,
,
где N – объем партии устройств. Согласно условию, N=300, поэтому
![]() .
.
Таким образом, из партии из 300 устройств ко времени t 96 из них будут работоспособны.
Глава 2
Требуется:
рассчитать среднюю наработку до отказа
![]() рассматриваемых объектов (топливных
форсунок). Первоначальные вычисления
произвести непосредственно по выборочным
значениям
рассматриваемых объектов (топливных
форсунок). Первоначальные вычисления
произвести непосредственно по выборочным
значениям
![]() ,
а затем с использованием статистического
ряда.
,
а затем с использованием статистического
ряда.
Решение:
Для вычисления среднего значения случайной величины воспользуемся формулой:
![]() ,
,
где
![]() равно числу значений
.
равно числу значений
.
Подставляя данные, получим:
![]()
![]() .
.
Упростить и ускорить
вычисления можно путем преобразования
наблюдения в статистический ряд. Для
этого весь диапазон значений
необходимо разделить на
![]() интервалов (разрядов) и подсчитать число
значений
интервалов (разрядов) и подсчитать число
значений
![]() ,
приходящееся на каждый разряд. Результаты
данной операции приведены в таблице 1.
,
приходящееся на каждый разряд. Результаты
данной операции приведены в таблице 1.
Таблица 1.
Преобразование значений наработки на отказ в статистический ряд.
i |
Интервал ч, 103 |
Число попаданий на интервал ni |
Статистическая вероятность qi |
1 |
|
5 |
0,1 |
2 |
|
15 |
0,3 |
3 |
|
20 |
0,4 |
4 |
|
10 |
0,2 |
Интервал
ч, 103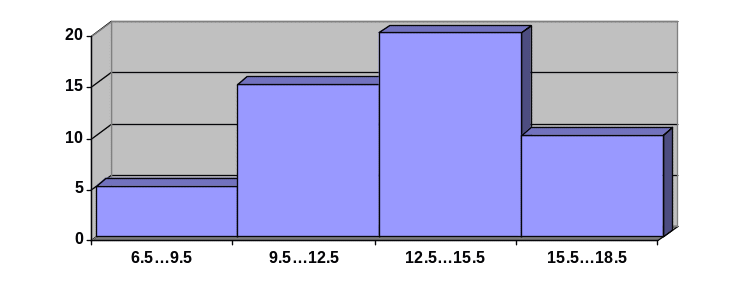
Гистограмма 1. Количество попаданий на интервал.
В данном случае
указаны результаты систематизации в
виде статистического ряда 50 значений
случайной величины, распределенной в
интервале [![]() ч;
ч;![]() ч]
при условии
ч]
при условии
![]() ч.
ч.
Правильность подсчетов определяем, используя следующее соотношение:
![]() ,
,
где - число попаданий значений случайной величины в интервал.
Подставляя полученные значения:
![]() .
.
Статистическая
вероятность
![]() попадания случайной величины в
попадания случайной величины в
![]() -ый
интервал рассчитывается так:
-ый
интервал рассчитывается так:
![]() .
.
Правильность определения вероятностей можно проверить по формуле:
![]() ,
,
где - число интервалов. Подставляя значение вероятностей, получим:
![]() ,
,
что подтверждает правильность расчетов.
Для расчетов среднего значений случайной величины используется формула:
![]() ,
,
где
![]() - середина интервала. Подставляя
полученные ранее значения, получим
- середина интервала. Подставляя
полученные ранее значения, получим
![]() .
.
Расчет с использованием формулы (4) вносит некоторую методическую ошибку. Однако ее значение обычно пренебрежимо мало. Эта ошибка оценивается по формуле
![]() ,
,
где
![]() и
и
![]() - средние значения, вычисленные по
формулам (3) и (4).
- средние значения, вычисленные по
формулам (3) и (4).
![]() ,
,
что укладывается в статистическую погрешность.
