Приборы и оборудование

Общий вид установки показан на рисунке (2)

Рис. 2.

На рисунке:

1. Окно;

2. Табло мА;

3.Табло мВ;

4. Кнопка Ток «+»;

5. Кнопка Ток «–»;

6. Кнопка «СБРОС»;

7. «ЭЛ. МАГНИТ - ДАТЧ. ХОЛЛА».

Установка состоит из объекта исследования и устройства измерительного.

Объект исследования конструктивно выполнен в виде сборного корпуса, в котором установлены электромагнит и датчик Холла. Сверху объект исследования имеет окно, через которое видны полюса электромагнита и плата с датчиком Холла.

На передней панели устройства измерительного размещены следующие органы управления и индикации:

- кнопки «СБРОС и ТОК» "+", "–" задают значение и направление тока через датчик Холла (при режиме работы с датчиком Холла) и катушку электромагнита (при режиме работы с электромагнитом);

Примечание: После нажатия кнопки «СБРОС» значение тока обнуляется, и направление тока меняется на противоположное.

- кнопка «ЭЛ. МАГНИТ - ДАТЧ. ХОЛЛА» переключает режимы работы с датчиком Холла и электромагнитом, что индицируется соответствующим светодиодом.

- табло мА и мВ индицируют значения тока через датчик Холла либо катушку электромагнита (в зависимости от режима работы) и э.д.с. Холла.

На задней панели устройства измерительного расположен выключатель «СЕТЬ».

Лабораторная работа №3 исследование температурной зависимости металлов и полупроводников

Цель работы: изучение температурной зависимости сопротивления металлов и полупроводников.

Содержание работы

Все твердые тела по способности проводить электрический ток делятся на металлы, полупроводники и диэлектрики. Диэлектрики имеют полностью заполненную валентную зону и пустую зону проводимости и практически не проводят электрический ток.

Разрешенные зоны металлов заполнены частично, что приводит к существованию электропроводности в этих материалах. Проводимость металлов с повышением температуры уменьшается по линейному закону:

(1)

где ₀ = const,  - температурный коэффициент сопротивления.

Полупроводники образуют средний класс между металлами и диэлектриками и способны проводить электрический ток при Т>0 К. При более низких температурах полупроводник является изолятором. Проводимость полупроводников при повышении температуры растет по экспоненциальному закону:

(2)

где ₀, ₀’ -некоторые константы; E - ширина запрещенной зоны; E’- энергия ионизации атомов примеси; k - постоянная Больцмана; T - абсолютная температура.

Анализировать температурную зависимость проводимости твердых тел возможно посредством рассмотрения концентрации носителей тока n и их подвижности u:

 = qnu, (3)

Носителями заряда в металлах являются электроны, и проводимость главным образом определяется их подвижностью, которая линейно уменьшается с ростом температуры.

Полупроводники имеют два типа носителей заряда - электроны и дырки, что усложняет характер их проводимости:

 = qn (u_n+ u_p), (4)

Температурная зависимость подвижности в полупроводниках определяется процессами рассеяния и выражается следующей формулой:

u = AT^-3/2 + BT^3/2, (5)

где А и В - некоторые константы.

При низких температурах носители заряда менее подвижны, и характер проводимости определяется рассеянием на примесях (второе слагаемое в (5)). При высоких температурах основную роль играет рассеяние на тепловых колебаниях решетки, и доминирует первое слагаемое.

Концентрация носителей заряда в полупроводнике экспоненциально зависит от температуры, и эта зависимость является решающей в определении проводимости по сравнению со степенной зависимостью подвижности. В формуле (2) первое слагаемое отвечает собственной проводимости и преобладает при высоких температурах, второе - при низких температурах в примесном полупроводнике.

Практически в эксперименте мы измеряем зависимость сопротивления от температуры, что позволяет нам с учетом формулы:

(5а)

убедиться, что для проводящего образца длиной l и поперечным сечением S сопротивление (5а) будет зависеть от температуры образца следующим образом (рис.1, где 1 - металл, 2 - полупроводник):

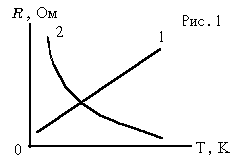
Рис. 1

и проверить справедливость формул (1) и (2) , а также рассчитать некоторые зонные параметры полупроводника.

В данной работе вычисляются следующие параметры

1.Температурный коэффициент сопротивления металла вычисляется по формуле (6):

(6)

где R₀ - сопротивление проводника при t = 0 град Цельсия.

Этот коэффициент численно равен значению изменения сопротивления проводника при нагреве на 1град Цельсия, деленному на сопротивление проводника при t = 0 град Цельсия.

2. Ширина запрещенной зоны полупроводника.

Для собственных полупроводников второе слагаемое в (2) отсутствует, что позволяет после логарифмирования (2) записать c учетом формулы (5):

(2а)

Последнее выражение в координатах lnR и представляет собой уравнение прямой, тангенс угла наклона которой можно определить по графику, построенному по экспериментальным точкам (рис.2):

Рис. 2

Это позволяет вычислить ширину запрещенной зоны:

(7)

Для примесного полупроводника при вычислении необходимо воспользоваться линейной частью зависимости lnR = f(1/T) , расположенной в области малых значений 1/T (т.е. в области высоких температур.

3. Энергия ионизации атомов примеси.

Для полупроводников, имеющих примеси, проводимость при низких температурах определяется в основном проводимостью примеси. Пренебрегая при низких температурах первым слагаемым в (2), после логарифмирования и подстановки в (5) получаем (2а’):

(2a')

Следовательно, при низких температурах получаем зависимость, аналогичную рис.2, позволяющую вычислить энергию ионизации атомов примеси по формуле (7а):

(7a)

4. Энергия Ферми.

В собственных полупроводниках уровень Ферми располагается в середине запрещенной зоны. Следовательно, определив ширину запрещенной зоны, можем рассчитать энергию Ферми:

(8)