величина давления в какой‑нибудь одной точке, в основном вдалеке от обтекаемого тела.

Начальные условия фигурируют лишь в нестационарных задачах и представляют собой задание пространственных распределений скоростей и температур в некоторый «начальный» момент времени.

Элементы теории подобия

Ввиду невозможности получить точное решение уравнений Навье–Стокса и уравнения энергии прибегают либо к приближенным решениям, либо к экспериментам на моделях. В последнем случае возникает вопрос об условиях подобия для обтекания натурного объекта и его модели. Будем считать, что два физических явления подобны, если отношения сходственных физических величин одинаковы в сходственные моменты времени во всех сходственных точках пространства. Другими словами, физические явления подобны, если любое из них может быть получено из другого путем изменения каждойиз характеризующих явление величин в одинаковое число раз. Следовательно, подобные физические явления описываются одними и теми же дифференциальными уравнениями, отличающимися только постоянными и одинаковыми при всех членах множителями. Если эти дифференциальные уравнения записать в безразмерном виде, то для двух подобных течений эти уравнения окажутся совершенно идентичными. Эти соображения являютсяосновой теории подобия.

Приведем к безразмерному виду уравнение Навье–Стокса (2.26'), для чего введем масштабы переменных величин, которым припишем индекс «нуль». Тогда (2.26') можно представить следующим образом:

Разделив все это выражение на величину₀w₀² / l₀,   пропорциональную конвективной силе инерции, получим:

Это уравнение содержит безразмерные комплексы, являющиеся критериями подобия, которым присвоены следующие названия:

l₀ / (w₀ t₀) = Sh  –число Струхаля, показывающее отношение локальной силы инерции, вызванной неустановившимся характером движения, к конвективной силе инерции;

(l₀ f₀) / w₀² = Fr  –число Фруда, показывающее отношение силы веса (объемной внешней силы) к конвективной силе инерции, т. е. во сколько раз потенциальная энергия больше кинетической;

P₀ / ₀ w₀²) = Eu  –число Эйлера, показывающее отношение силы гидродинамического давления к конвективной силе, т. е. во сколько раз давление больше скоростного напора;

_/ (l₀ ₀ w₀) = (l₀ w₀) / v₀ = Re  –число Рейнольдса, показывающее отношение сил вязкости и конвективных сил.

При получении указанных критериев все действующие на жидкость силы сравнивались с конвективными силами инерции. Можно, конечно, сравнивать и другие пары сил. Тогда получим и некоторые иные критерии, но все они будут выражаться через те же критериальные комплексы. Использование таких новых критериев не имеет практического смысла. Моделировать надо по главным силам, к которым в подавляющем числе задач и относятся конвективные силы инерции.

Для сжимаемой жидкости число Эйлера может быть выражено так:

где

т. е. в случае газовых течений появляются два дополнительных критерия: 1) число Пуассона   (C_p/C_v);   2) число Маха   (M =w/a).

Выполнить условия полного подобия очень трудно. Если натурный объект работает в какой‑либо среде, то при переходе к модели (с меньшими размерами) надо изменять скорость исходя из следующих требований:

Одновременное выполнение этих требований невозможно. Однако в большинстве случаев добиваться полного подобия и не надо. Обычно в каждой конкретной задаче некоторые члены уравнения (2.26') либо равны нулю, либо малы.

П р и м е р  1.  Для самолета число Фруда не имеет значения, так как сила тяжести, действующая на частицы воздуха, обтекающего самолет, мала. Если самолет движется с небольшой скоростью   (M   1),   то сжимаемости воздуха не происходит и поэтому нет необходимости в выполнении требования   M = idem.   Наконец, в случае установившегося движения самолета отпадает и требование   Sh = idem.  Здесь достаточно удовлетворить условия геометрического и кинематического подобий и требование   Re = idem.   Испытание модели такого самолета в аэродинамической трубе необходимо вести при очень большой скорости потока   [w_м = w_н (l_н / l_м)].   Размеры l_м   не должны быть очень маленькими, иначе   w_м   может возрасти настолько, что нельзя будет пренебречь сжимаемостью, т. е. нарушится одно из принятых условий (M   1).   Поэтому дозвуковая аэродинамическая труба должна иметь относительно большие размеры. Известный способ обойти эту трудность – построить трубу с высоким давлением воздуха, в которой малый размер модели   [при   Re = _ / (l₀ ₀ w₀)]компенсируется повышенной плотностью. Иногда модель испытывают не в воздухе, а во фреоне, используя малую вязкость последнего.

П р и м е р  2.  Исследуют сверхзвуковой летательный аппарат с большим сопротивлением давления. В этом случае сопротивление трения (вязкость) не играет роли, т. е. нет необходимости выдерживать условия   Fr = idem   и   Sh = idem. Основным определяющим критерием является   M = idem   при    = idem.   Это позволяет производить моделирование в сверхзвуковой трубе малых размеров.

П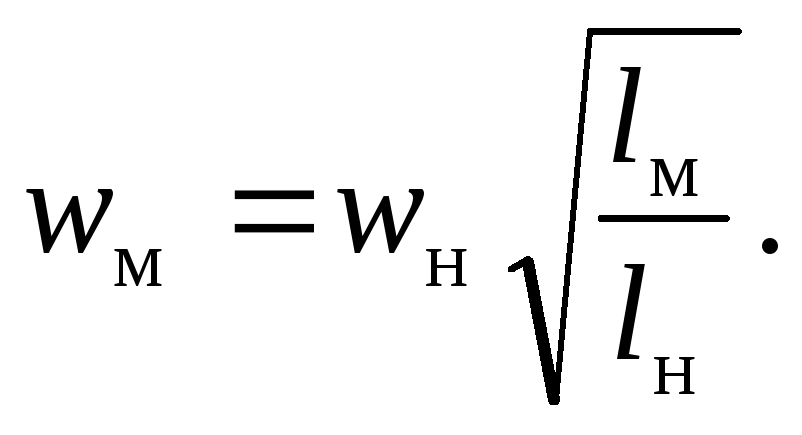р и м е р  3.  Рассмотрим корабль не очень обтекаемой формы. Он порождает большие волны, и в таком случае сопротивление трению имеет второстепенное значение по сравнению с волновым сопротивлением (затратой энергии на преодоление силы тяжести воды). Определяющим критерием является число Фруда. При испытании модели корабля в гидроканале скорость ее движения следует принять меньшей, чем у натуры, в корень квадратный раз из отношения линейных размеров:

Иногда нельзя добиться приближенного подобия, выдерживая постоянство одного критерия. Например, при моделировании хорошо обтекаемого летательного аппарата необходимо, чтобы   M = idem  и  Re = idem,  так как сопротивления давлению и трению в данном случае соизмеримы. В подобном случае нужна сверхзвуковая труба больших размеров.

Для приближенного моделирования судна обтекаемой формы требуется выполнить условия:   Fr = idem,    Re = idem.

Рассмотрим теперь уравнение энергии (2.40). Приведем его к безразмерному виду, причем за масштаб температуры примем разность температур набегающего потока (вдали от тела) и стенки тела  T₀ = T_ – T_ст .Также исследуем установившийся режим (учет нестационарного члена дает, как и раньше, число Струхаля). Тогда (2.40) можно представить в следующем виде:

После деления этого уравнения на общий множитель левой части получим:

В данном уравнении все виды тепловых потоков выражены в долях от конвективного тепла.

Тепловое подобие двух процессов осуществляется при наличии равенства в обоих течениях полученных трех безразмерных комплексов:   1) P₀ / (₀ C_p T₀); 2) / (l₀ ₀ C_p w₀);   3) (w₀) / (l₀ ₀ C_p T₀).   Исследуем их.

1‑йкомплекс:

где      –   температурный критерий   [ = w₀² / (C_p T₀)],   который пропорционален   w₀²   и учитывает отношение работы сжатия, осуществляемой динамическим давлением, к конвективному тепловому потоку. Поэтому он существен при больших скоростях потока.

2‑йкомплекс(выражает собой отношение тепла, переносимого теплопроводностью к конвективному потоку):

где    / (C_p   –   число Прандтля   (Pr),   характеризующее связь между теплоемкостью, теплопроводностью и вязкостью.

Произведение чисел Прандтля и Рейнольдса называютчислом Пекле, или критерием Пекле(Pe):

Он широко используется при моделировании процессов теплообмена.

3‑йкомплекс(представляет собой отношение рассеиваемого тепла к конвективному потоку и не приводит к новым комплексам):