Раздел 5.

ПЛОСКОЕ БЕЗВИХРЕВОЕ ДВИЖЕНИЕ СЖИМАЕМОГО ГАЗА

Вывод дифференциального уравнения

Д ля анализа плоского течения сжимаемого газа воспользуемся уравнением движения идеальной жидкости и спроектируем его на оси координат. Пренебрегая силой тяжести и считая движение установившимся, получим:

У равнение неразрывности

з апишем в следующем виде:

Д ля безвихревого, т. е. потенциального, течения газа справедливо уравнение адиабаты   P / ^ = const,   т. е.   P = P().   Теперь получим:

где   a   – скорость звука в данной точке потока.

П одставив значения (5.3) в уравнение движения (5.1), получим:

У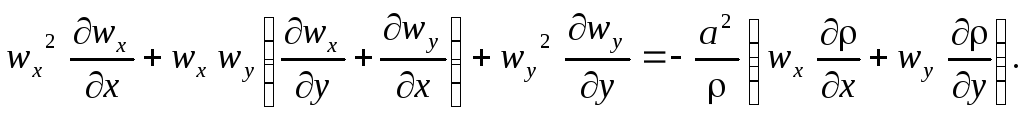 множив уравнение (5.4) на   w_x,   а уравнение (5.5) на   w_y   и сложив их, получим:

З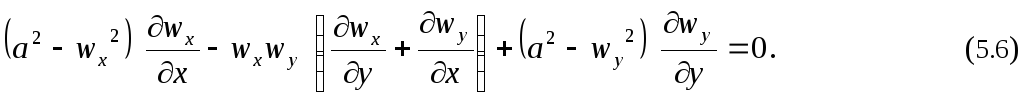 аменив сумму справа из уравнения неразрывности (5.2), имеем

Итак, мы вывели основное дифференциальное уравнение газовой динамики для двухмерного (плоского или пространственного осесимметричного) установившегося потока. Так как это уравнение связывает между собой скорости, то его называют основным кинематическим уравнением.

Е сли течение потенциальное, то

и тогда (5.6) имеет вид

Это – основное уравнение газовой динамики для двухмерного потенциального установившегося течения , или уравнение для потенциала скоростей. В частном случае малых скоростей движения газа   (w_x << a,   w_y <<  a)   данное уравнение – (5.7) – переходит в уравнение Лапласа, определяющее движение несжимаемой жидкости.

Уравнение (5.7) нелинейно, так как его коэффициенты зависят от искомой функции      (точнее, от ее частных производных по   x   и   y). Поэтому сумма частных решений не дает решения данного уравнения, т. е. мы не можем «накладывать» различные потоки, или, другими словами, «расслаивать» сложный поток на простые составляющие.

Решения уравнения для потенциала скоростей

Решения уравнения (5.7)    =  (x, y)   геометрически изображаются в пространстве, определяемом координатной системой   x, y, ,   в виде интегральных поверхностей. Эти решения ищут в окрестностях некоторой (начальной) кривой   y = y (x),   где известно значение некоторой функции    и первых производных     x   или     y. Отыскание таких решений составляет содержание задачи Коши.

Итак, в случае двух независимых переменных задача Коши сводится к отысканию интегральной поверхности, проходящей через заданную кривую. Если заданная кривая имеет касательную, то в некоторой окрестности этой кривой задача Коши всегда имеет решение, и притом единственное.

Д ля решения задачи Коши представим (5.7) в виде

где   A = wx² – a²;   B = wx wy;   C = wy² – a²;   u, s, t   – вторые производные от  .

Е сли мы хотим найти   u, s, t   через   wx   и   wy,   то нам не хватает еще двух уравнений. Введем обозначения

Т огда на исходной кривой по определению полного дифференциала функций двух независимых переменных будем иметь

Т аким образом, система уравнений для определения вторых производных будет иметь следующий вид:

С истема (5.10) решается относительно неизвестных   u, s, t   при помощи определителей. Главный определитель –   ,   частные определители –   u, s, t.

Из этих соотношений следует, что если главный определитель      не равен нулю на начальной кривой, то вторые производные   u, s, t   определяются однозначно.

Р ассмотрим случай, когда исходная кривая выбрана таким образом, что на ней главный определитель системы (5.10) равен 0:

И з курса математики известно, что при условии    = 0   [см. систему (5.10)] на кривой, выраженной уравнением (5.11), вторые производные   u, s, t   либо определяются неоднозначно, либо вообще не могут быть определены через , P, q.

Рассмотрим решение уравнения (5.11):

Эти равенства определяют наклон касательной в каждой точке начальной кривой, на которой главный определитель    = 0.

Нетрудно заметить, что равенства (5.12) являются дифференциальным уравнением  двух  семейств  вещественных  кривых,  если    B² – AC > 0.    Такие

69