2. Степенные средние

12. Абсолютные и относительные показатели вариации

Вариация - колеблемость, изменяемость величины признака у единиц совокупности.

Абсолютные показатели вариации измеряются в тех же единицах, что и признак

1. Размах вариации (R) представляет собой разность между максимальным и минимальным значениями признака в изучаемой совокупности.

(R = Хmax- Xmin)

2. Среднее линейное отклонение представляет собой среднюю арифметическую из абсолютных значений отклонений отдельных вариантов от их средней арифметической:

где d - среднее линейное отклонение;

| |-абсолютное значение (модуль) отклонения варианта от средней арифметической;

f-частота.

3. Дисперсия ( ) - средняя из квадратов отклонений вариантов значений признака от их средней величины:

Или для не сгруппированных данных,

для сгруппированных данных.

4. Среднее квадратическое отклонение представляет собой корень квадратный из дисперсии:

Относительные величины представляют собой отношение абсолютных величин к средней величине или медиане:

1. коэффициент осцилляции

2. относительное линейное отклонение

3. Коэффициент вариации

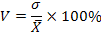
13. Виды дисперсий, правило сложения дисперсий. Дисперсия альтернативного признака.

Виды дисперсий:

1. Групповая

средняя величина признака

2. Внутри групповая (средняя из групповых)

n_i - число единиц в группе

2. Межгрупповая

общая средняя

2. общая дисперсия

Данное соотношение отражает закон, который называют правилом сложения дисперсий . Согласно этому закону (правилу), общая дисперсия , которая возникает под влиянием всех факторов, равна сумме дисперсий , которые появляются как под влиянием признака-фактора, положенного в основу группировки, так и под влиянием других факторов. Благодаря правилу сложения дисперсий можно определить, какая часть общей дисперсии находится под влиянием признака-фактора, положенного в основу группировки.

2. Эмпирический коэффициент детерминации представляет собой долю межгрупповой дисперсии в общей дисперсии .

2. Теснота связи между факторным и результативным признаком оценивается на основе эмпирического корреляционного отношения:

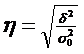
Дисперсия альтернативного признака .

Альтернативными называются 2 взаимоисключающих друг друга признака . То признаки , которыми каждая отдельная единица совокупности либо обладает, либо не обладает. Наличие альтернативного признака принято обозначать через единицу, а отсутствие через 0. Долю единиц обладающих данным признаком обозначают через p, а долю единиц на обладающих данным признаком обозначают через q. При этом p+q=1.

Дисперсия альтернативного признака определяется по формуле:

14. Понятие о выборочном наблюдении. Основные способы формирования выборочной совокупности.

Выборочное наблюдение – это не сплошной метод наблюдения, при котором исследуется только часть единиц совокупности, отобранная на основе положений случайного отбора.

Совокупность, из которой отбирают единицы для исследования – генеральная совокупность.

Часть единиц, отобранная для исследования – выборочная совокупность (выборка).

Основные способы формирования выборочной совокупности:

1. Случайный на повторной и бесповторной основе (принцип жеребьевки: бесповторный- вытянули и убрали, повторный - вытянули и положили обратно)

2. Механический (применяется, когда генеральная совокупность каким-либо способом упорядочена (например, списки избирателей по алфавиту, телефонные номера, номера домов, квартир). Отбор единиц осуществляется через определенный интервал, который равен обратному значению процента выборки.)

3. Типический (обследуемая совокупность предварительно разбивается на однородные, однотипные группы. Например, при обследовании предприятий это могут быть отрасли, подотрасли, при изучении населения – районы, социальные или возрастные группы. Затем осуществляется независимый выбор из каждой группы механическим или собственно-случайным способом.)

4. Серийный (применяется в случае, когда генеральная совокупность разбита на серии или группы до начала выборочного обследования. Этими сериями могут быть упаковки готовой продукции, студенческие группы, бригады.)