3.2 Зависимость коэффициента экранирования магнитного экрана от напряженности внешнего магнитного поля

Коэффициент экранирования можно вычислить, как

.

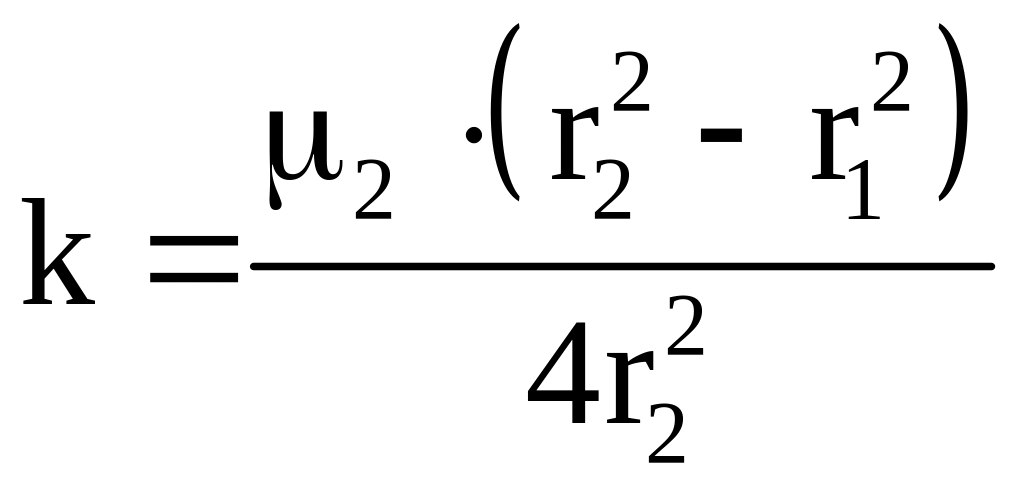Используя различные значения μ, получим зависимость k(H_o). Данные занесем в таблицу 3.1 и построим график.

Ho, А/см	0	1,5	7	14,11	20	77	130	250,6	546,6
μ	0	63,5	95	287	326	141	90,4	50,4	25,1
k(H0)	0	0,0273	0,0408	0,1234	0,1401	0,06	0,0388	0,0216	0,0107

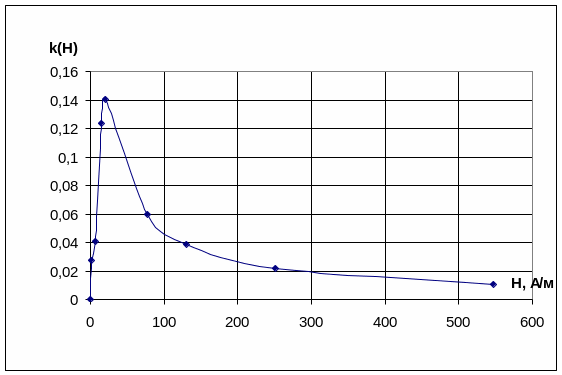
Рис. 3.3 Зависимость коэффициента экранирования от напряженности внешнего магнитного поля

3.3 Расчет параметров магнитного экрана имеющего минимальные габаритные размеры и вес

Определим значение относительной магнитной проницаемости при напряженности H₀ = 42,5 A/м для различных видов стали и занесем данные в таблицу 3.2. Затем рассчитаем радиус внешнего экрана для каждого значения относительной магнитной проницаемости по формуле

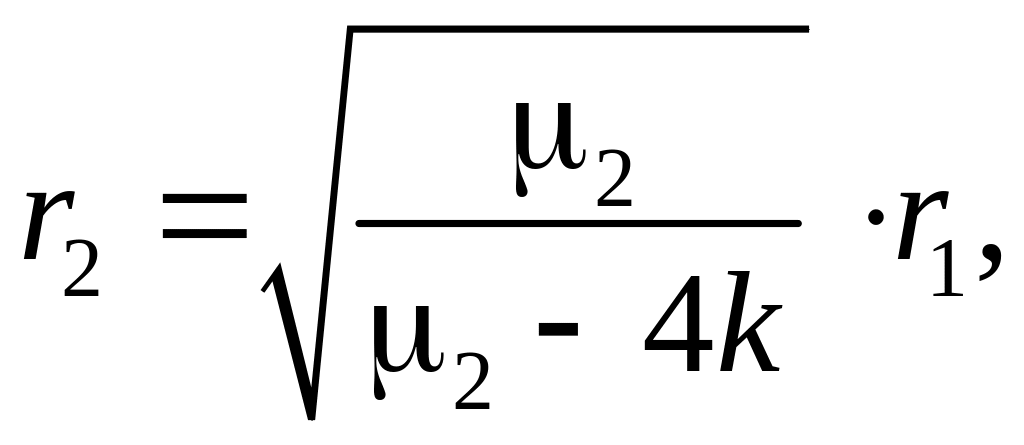
и результаты вычислений также сведем в таблицу 3.2.

Вид стали	Сталь 10	Сталь ШХ-15	Сталь 20	Сталь Ст3	Электротехническая сталь
μ	249	265	302	390	403
r2	0,3203	0,32029	0,320254	0,320191	0,3201907

Анализируя полученные значения определяем, что минимальные размеры соответствуют магнитной проницаемостью 403 для типа Электротехническая сталь.

Таким образом, минимальный внешний радиус экрана

0,3201907 м.

Вес магнитного экрана равен

кг.

Выводы:

• Оптимальные линейные размеры и вес магнитного экрана для материала Сталь ШХ-15: r₁ = 0,32 м, r₂ = 0,32028 м, m = 0,8781 кг ;

• Минимальные линейные размеры и вес магнитного экрана: r₁ = 0,32 м, r₂ = 0, 3201907 м, m = 0,59801 кг ;

• Построили зависимость коэффициента экранирования от напряженности внешнего магнитного поля.

4. Расчет электромагнитного поля элементарного излучателя Исходные данные

По отрезку прямолинейного провода длиной l = 42 мм проходит переменный ток i=0,25sin(6,9∙10⁶)t, A. Среда, окружающая провод, имеет 4,4. Считать, что со средней точкой отрезка провода совмещено начало отсчета сферической системы координат и что ось отсчета углов совпадает с положительным направлением тока в проводе.

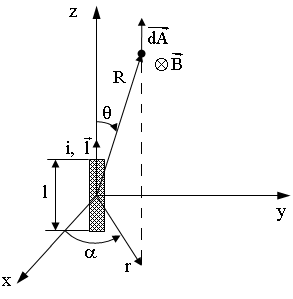
Рис.19. Исходная схема

4.1.Вывод аналитического выражения для определения напряженностей электрического и магнитного поля излучаемой электромагнитной волны в ближней и дальней зоне

Составляющая векторного потенциала от элемента линейного тока записывается как

В переменном магнитном поле с учетом явления запаздывания имеем

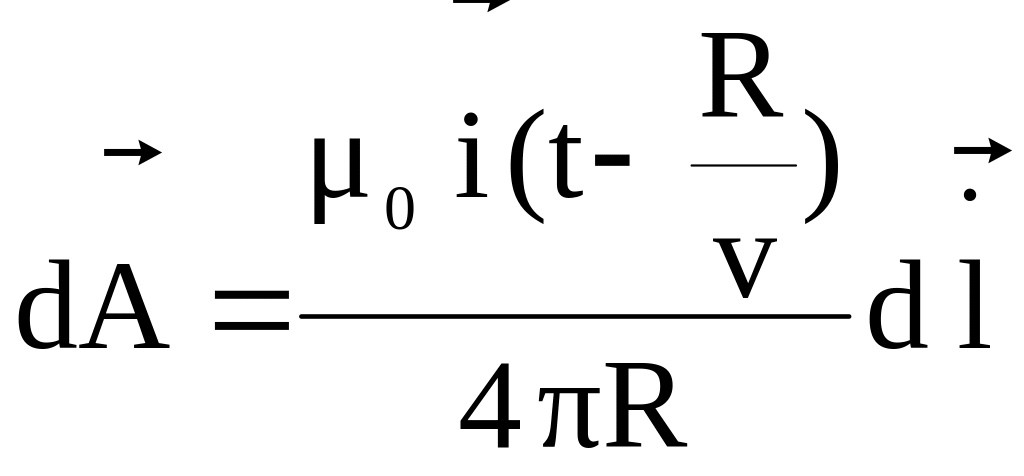
Ток представим в показательной форме , и для упрощения будем обозначать через , тогда

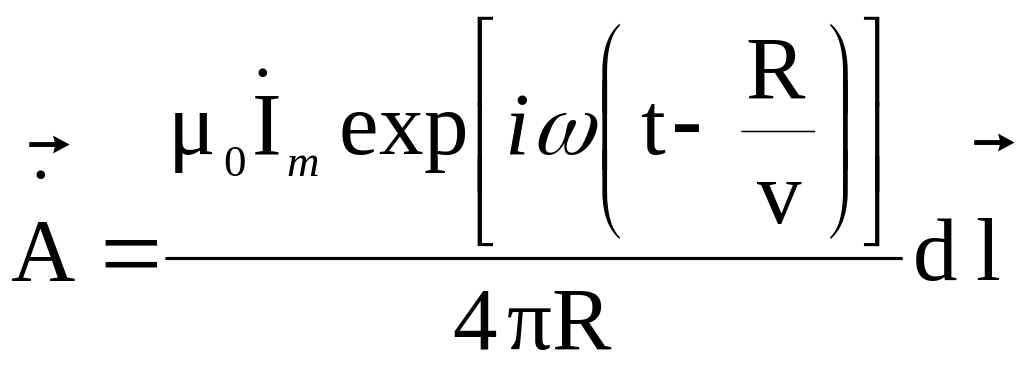
или, если исключить множитель ,

.

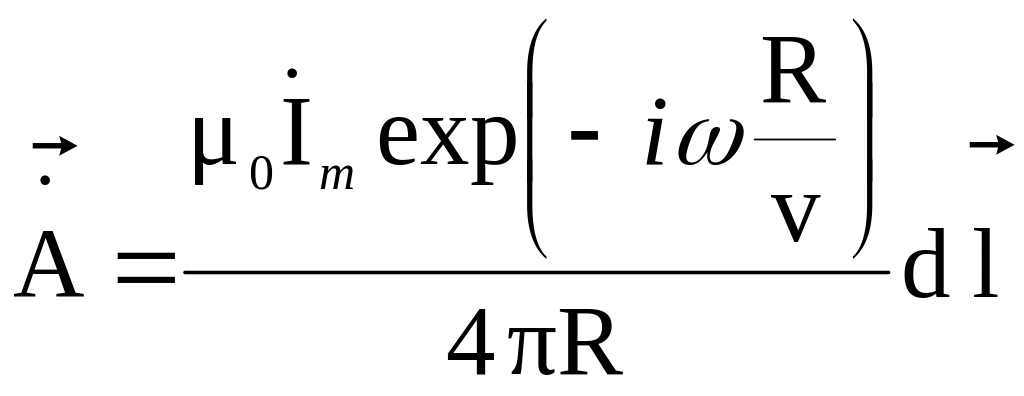Магнитную индукцию найдем из соотношения . Выражение для комплекса магнитной индукции в сферических координатах будет выглядеть следующим образом

,

для мгновенных значений

.

Напряженность магнитного поля равна

В соответствии с первым уравнением Максвелла

,

так как в рассматриваемой точке пространства =0, то

.

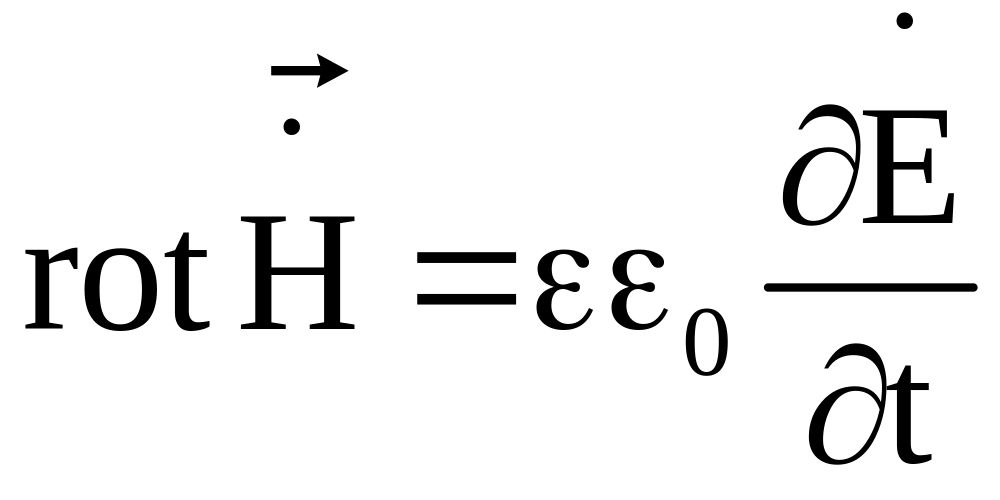Тогда

.

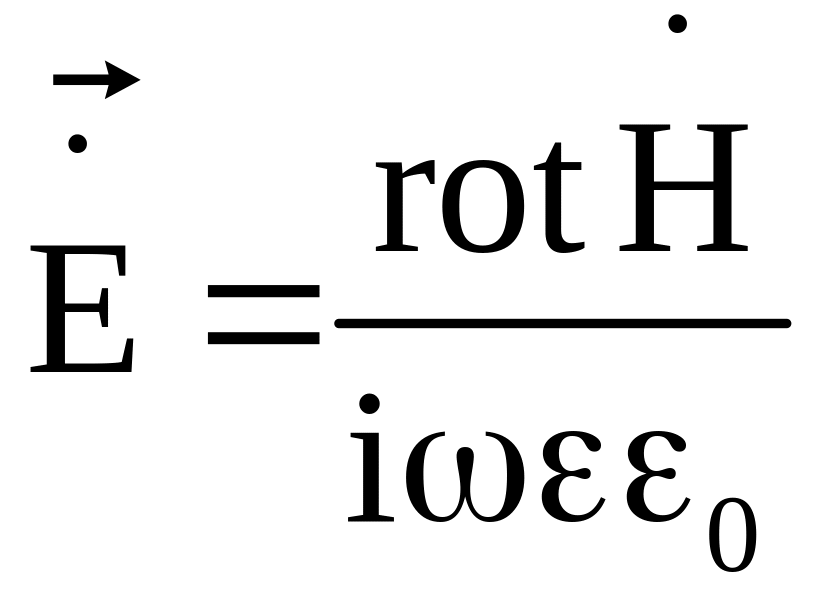Отсюда

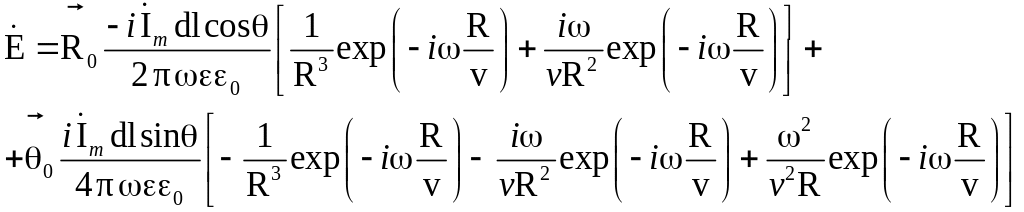
Для мгновенных значений

В ближней зоне, где значение параметра R << λ/2π, для электромагнитного поля элемента проводника с током имеем следующие выражения:

,

,

.

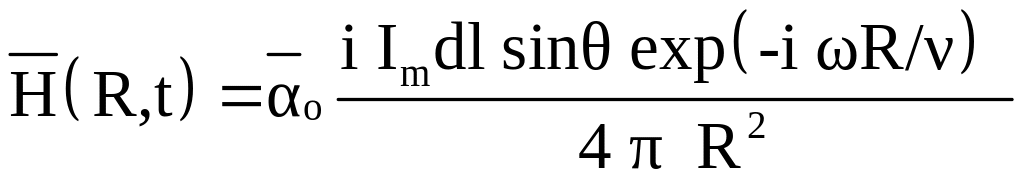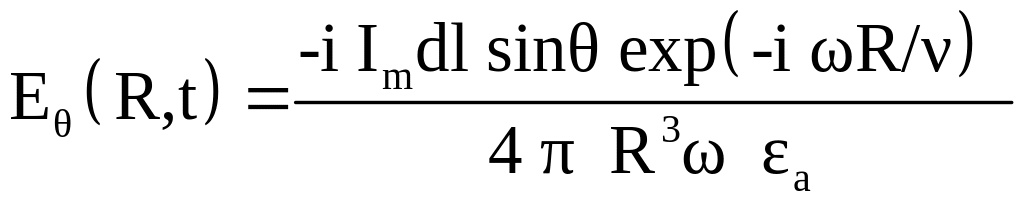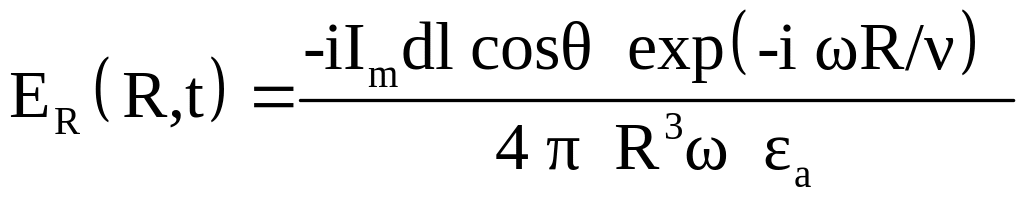Если значение параметра R >> λ/2π, то есть, имеем дело с дальней зоной, тогда для электромагнитного поля элемента проводника с током получаем:

,

.

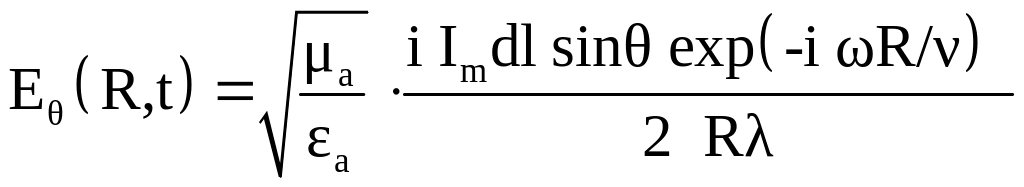Из условия ω = 3,5∙10⁶ рад/с
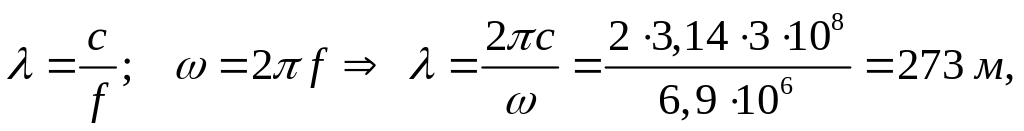