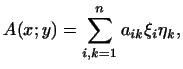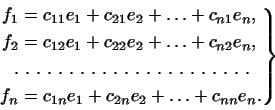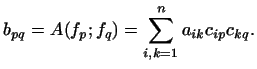3 Матрица билинейной формы.
Мы определили билинейную форму аксиоматически. Выберем теперь в -мерном пространстве какой-либо базис и выразим билинейную форму через координаты и векторов и в этом базисе. Мы имеем:
В силу свойств 1 и 2 билинейной формы
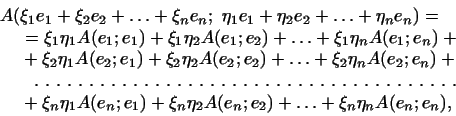
или, короче
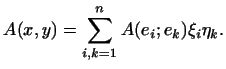
Обозначим
постоянные 
через 
.
Тогда имеем:
при заданном базисе всякая билинейная форма в -мерном пространстве может быть записана в виде
|
(3) |
где -- координаты вектора , а -- координаты вектора в данном базисе. Числа зависят от выбора базиса и вычисляются по формулам
|
(4) |
Матрица 
называется матрицей
билинейной формы
в
базисе
.
Таким образом, в каждом базисе билинейная форма определяется своей матрицей .
Пример
3
Пусть
--
трехмерное пространство, векторами
которого являются тройки чисел 
.
Зададим в
билинейную
форму
формулой
Возьмем в в качестве базиса три вектора
Найдем
матрицу 
билинейной
формы
в
этом базисе. В силу (4) получим:
т.е.
Таким
образом, если обозначить через 
)
и 
координаты
векторов
и
в
базисе 
,
то
4 Преобразование матрицы билинейной формы при изменении базиса.
Пусть
даны в
-мерном
пространстве два базиса:
и 
.
Пусть векторы
выражаются
через векторы базиса
формулами
|
Таким
образом, 
--
координаты вектора 
в
базисе
.
Матрицу
назовем матрицей перехода от базиса к базису .
Пусть
есть
матрица билинейной формы
в
базисе
,
а 
--
матрица той же билинейной формы в
базисе
.
Наша задача состоит в том, чтобы по
матрице
найти
матрицу 
.
По
определению [формула (4)] 
,
т.е. 
--
значение билинейной формы
при 
, 
;
для того чтобы найти его, воспользуемся
формулой (3), подставив в нее
вместо
и
координаты
векторов 
и 
в
базисе
,
т.е. числа 
и 
.
Получим:
|
(6) |
Это есть искомая формула.
Запишем
ее в матричной форме. Для этого положим 
;
таким образом, 
являются
элементами
матрицы 
,
транспонированной к матрице 
.
Тогда
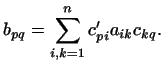
В матричной форме это означает 2.13:
|
(7) |
Итак: если
и 
суть
матрицы билинейной формы
соответственно
в базисах
и
,
то 
,
где
--
матрица перехода от базиса
к
базису
,
а
--
матрица, транспонированная к матрице
.
5 Квадратичные формы.
Определение
4.4
Пусть
--
симметрическая билинейная форма.
Функция 
,
которая получается из
,
если положить 
,
называется квадратичной
формой.
называется билинейной формой, полярной к квадратичной форме .
Требование симметричности формы в определении квадратичной формы оправдывается следующим предложением, которое без этого было бы неверно.
Полярная форма однозначно определяется своей квадратичной формой .
Доказательство. Из определения билинейной формы легко следует, что
Отсюда
в силу симметрии (т.е. равенства 
)
получаем:
В правой
части этого равенства стоят значения
квадратичной формы; следовательно, мы
доказали, что билинейная форма
определяется
своей квадратичной формой 2.14.
Выше мы уже доказали, что всякая симметрическая билинейная форма записывается через координаты векторов и в виде
где . Поэтому:
всякая квадратичная форма при заданном базисе выражается формулой
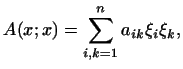
где . Введем еще одно важное
Определение
4.5
Квадратичная форма
называется положительно
определенной, если для любого вектора 
Пример
4 
является,
очевидно, положительно определенной
квадратичной формой.
Пусть -- положительно определенная квадратичная форма и -- ее полярная форма. В силу сформулированных выше определений это означает:
1 .
2
.
3
.
4
и 
при
.
Мы видим, что эти условия совпадают с аксиомами скалярного произведения, сформулированными в 2. Следовательно, скалярное произведение есть билинейная форма, соответствующая положительно определенной квадратичной форме, и любая такая форма может быть принята за скалярное произведение.
Поэтому мы можем определить евклидово пространство следующим образом.
Евклидовым пространством называется аффинное пространство, в котором выбрана какая-нибудь фиксированная положительно определенная квадратичная форма . Значение соответствующей 2.15ей билинейной формы считается при этом скалярным произведением2.16векторов и .