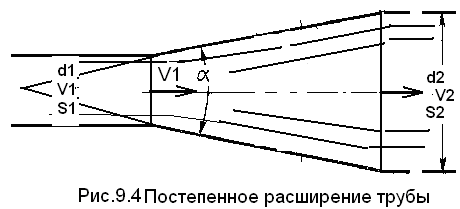
9.3. Постепенное расширение трубы

Местное сопротивление, при котором труба постепенно расширяется, называется диффузором. Течение жидкости в диффузоре сопровождается уменьшением скорости и увеличением давления, происходит преобразование кинетической энергии жидкости в энергию давления.

Формула для определения сопротивления диффузора похожа на формула для определения потерь при внезапном расширении , где φд - коэффициент диффузора.

Функция φ_д=f(α) имеет минимум при угле α = 6º φ_д=0,2 (рис.9.5), для угла α = 10º φ_д=0,23-0,25.

Диффузор устанавливают для уменьшения потерь, возникающих при переходе от меньшего к большему диаметра трубы.

9.4. Внезапное сужение трубопровода

При внезапном сужении трубы потери энергии связаны с трением потока при входе в узкую трубу и с потерями на вихреобразование. Поскольку поток не обтекает входной угол, а срывается с него и сужается, поисходит вихреобразование. Кольцевое пространство вокруг суженной части потока заполнено завихренной жидкостью.

Относительно скорости в узком сечении V₁коэффициент сопротивления равен

(9.13)

Относительно скорости в широком сечении V₂

где ξ_суж - коэффициент сопротивления внезапного сужения зависящий от степени сужения и от сечения к которому приводится коэффициент,n=S₂/S₁- степень сужения.

9.5. Потери энергии при выходе из резервуара в трубу.

При выходе из резервуара в трубу больших размеров и при отсутствии закруглений входного угла, когда S₂>>S_{1 ,}отношениеS₂/S₁→0, для выхода из резервуара в трубу получим

коэффициент сопротивления ξ_в.р.тр.= 0,5.

Закруглением входного угла (входной кромки) можно значительно уменьшить потерю напора при входе в трубу.

9.6. Потери энергии при постепенном сужении трубы - конфузор.

Постепенное сужение трубы называется конфузором. Течение жидкости в конфузоре сопровождается увеличением скорости и падением давления. Давление жидкости в начале конфузора выше, чем в конце, поэтому причин к возникновению вихреобразований и срывов потока, как в диффузоре, нет.

В конфузоре имеются только потери на трение, и поскольку его длина невелика, обычно l/d≈ 3-4.сопротивление конфузора всегда меньше, чем диффузора и зависит от угла конфузора и его длины, обычные значения коэффициента ζ = 0,06-0,09. Например, для.

Расчет сопротивления конфузора производится по формуле для определения местных сопротивлений

Следует иметь ввиду, что значение ζ обычно связывается с узким сечением конфузора.

9.7.Поворот трубы

Местное сопротивление при повороте трубы на произвольный угол без закругления называется "колено". Потерю напора рассчитывают по формулеh = ξ_кV²/(2g).

Коэффициенты сопротивления колена круглого сечения определяют экспериментально, ξ_квозрастает с увеличением углаδ (рис.9.17) и при δ = 90° достигает единицы.

Величина коэффициента сопротивления может быть определена приближенно по формуле ζк =Sin²δ

Постепенный поворот трубы называется отводом. При достаточно большом его значении относительного радиуса кривизны отвода R/d, срыв потока устраняется полностью. Коэффициент сопротивления отводаξ_отв зависит от отношенияR/d, углаδ, а также от формы поперечного сечения трубы.