6.1.Уравнение Бернулли для потока реальной (вязкой) жидкости.

При движении реальной жидкости на преодоление сопротивлений, связанных с вязкостью, требуются затраты энергии, поэтому удельная энергия движущейся вязкой жидкости не остается постоянной, как в случае идеальной жидкости, а уменьшается вдоль потока.

При выводе уравнения Бернулли для потока вязкой жидкости вместо неравномерного распределения скоростей рассматриваются средние скорости и средние значения удельной энергии жидкости в данном сечении. Измерение скорости в различных точках сечения потока выполнить сложно, измерение средней скорости потока выполнить проще и они могут быть сделаны с большей точностью.

6.2. Мощность потока

Мощностью потока называется полная энергия, которую проносит поток через данное сечение в единицу времени.

Мощностью называется отношение работы, выполненной за определенный промежуток времни к длительности этого промежутка. Например, для гидроцилиндра

где давление p= ρgh, , работа А =pghS*L, массовый расходδQ_m=ρW/t = ρ(L*S)/t

Мощность элементарной струйки это произведение полной удельной энергии струйки жидкости в виде третьей формы уравнения Бернулли в данной точке

gН= gz + p/(ρ) + (V²/2),на элементарный массовый расход струйкиδQ_m=ρ(V*δS/δt).

δN = gH*δQ_m = (gz + p/ρ + v²/2)*ρ* v*δS=P*δQ

Мощность всего потока ,

6.3 Коэффициент Кориолиса

Для определения полной удельной мощности потока разделим мощность потока на средний массовый расход: Q_m = ρQ = ,где Q=Vср*S.

Умножив и разделив последний член на V, получим, переходя к напорам (третья степень в знаменателе получается умножением на скорость в составе расхода)

(6.6)

Коэффициент Кориолиса представляет собой отношение действительной кинетической энергии потока в данном сечении к кинетической энергии того же потока и в том же сечения, но при равномерном распределении скоростей, поскольку интеграл от dm = ρ*VdS– масса потока в данном сечении:

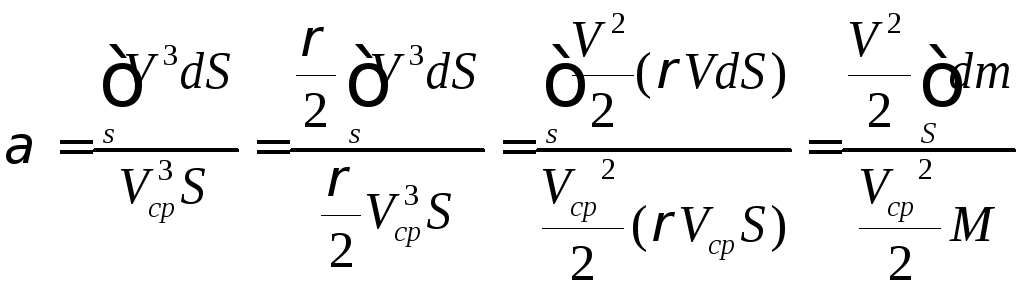
Возьмем два сечения реального потока, первое и второе, и обозначим средние значения полного напора жидкости в этих сечениях соответственно Н_ср1иН_ср2. Тогда

Н _ср1 = Н_ср2 + Σh_п, гдеΣh_п - суммарная потеря полного напора на участке между рассматриваемыми сечениями.

Это уравнение Бернулли для потока вязкой жидкости:

(6.8)

От уравнения для элементарной струйки идеальной жидкости это уравнение отличается четвертым членом - потерей полного напора, и коэффициентами Кориолиса, учитывающим неравномерность распределения скоростей. Скорости, входящие в это уравнение, являются средними скоростями в первом и тором сечениях потока.

Уравнение Бернулли для струйки идеальной жидкости - это закон сохранения механической энергии.

Уравнение Бернулли для потока реальной жидкости - уравнение баланса энергии с учетом потерь.

6.4 Гидравлические потери .

Гидравлические потери удельной энергии, выраженные напором или давлением, зависят от формы и размеров трубопровода, скорости течения и вязкости жидкости.

При турбулентном режиме движения жидкости гидравлические потери пропорциональны скоростям во второй степени, в единицах длины h _п = ζ V² _ср /(2g),

Безразмерный коэффициент потерь ζ - дзета называется коэффициентом сопротивления и равен отношению величины потерянного напора к скоростному напору.

Гидравлические потери разделяют на местные потери и потери на трение по длине.

Значение ζ вообще зависит от формы местного сопротивле­ния, шероховатости его стенок, условий входа и выхода из него жидкости и основного критерия динамического подобия напор­ных потоков - числа Рейнольдса.

Число Рейнольдса обычно относят к сечению трубопровода, в котором находится местное сопротивление

.

где V и Q - средняя скорость потока и расход в трубе; D - диа­метр трубы; ν- кинематическая вязкость жидкости.

Число Рейнольса определяет режим течения жидкости. При его значении меньше Re≤2300 режим течения жидкости называется ламинарным, от слова ламина – слой или слоистым.

Ламинарным движением жидкости называется режим ее течения упорядоченным слоями без ее перемешивания.

Струи жидкости, находящиеся на разном удалении от оси движутся с различными скоростями. Наибольшую скорость имеет осевая струйка, при стенках скорость равна нулю.

Увеличение скорости понижает устойчивость ламинарного течения и нарушает его режим. На устойчивость ламинарного режима оказывают влияние вязкость жидкости, плотность, скорость движения частиц, а также диаметр трубопровода.

При увеличении скорости струйки разрываются, разрыву предшествует образование волнообразных колебаний. При усилении колебаний струйка полностью перемешивается с окружающей жидкостью. Движение частиц производит впечатление беспорядочных вихрей. При числах Рейнольса больше Re>2300 режим течения жидкости становится турбулентным.

Турбулентным движением жидкости называется режим ее течения неупорядоченным слоями с их перемешиванием.