7.2 Гармонические колебания.

Уравнение 2-го Закона Нъютона в отсутствие сил трения для квазиупругой силы вида имеет вид:

или (* ) ,

здесь . Поскольку, >0, то -вещественная величина. Это линейное дифференциальное уравнение второго порядка с постоянными коэффициентами.

Такие уравнения решают с помощъю подстановки , -постоянная величина. После чего получают алгебраическое уравнение

с мнимыми корнями и , называемое характеристическим.

Его общее решение имеет вид: , где , -комплексные постоянные

Решение уравнения (*) имеет вид:

, где , -произвольные постоянные, которые для каждого конкретного колебания определяются начальными условиями: и при t = 0, -амплитуда колебаний;

-фаза, -начальная фаза, - период колебаний, равный .

Период находится из условия ,

Таким образом, смещение изменяется по закону или .Следовательно движение системы, под действием силы вида представляет собой гармоническое колебание. Его график показан на рисунке.

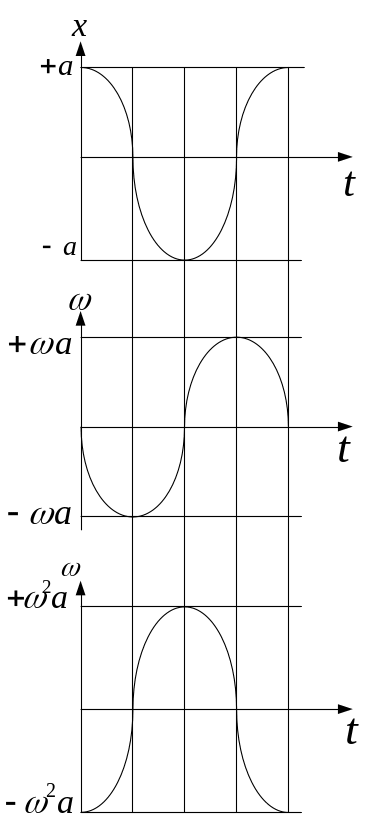
Рис.7,3

Выражение для скорости и ускорения системы имеют вид:

Квазиупругая сила является консервативной, поэтому полная механическая энергия гармонического колебания должна сохраняться. При колебаниях происходит превращение кинетической энергии в потенциальную и наоборот.

В крайних положениях системы: , в положении равновесия т.е.

Со временем 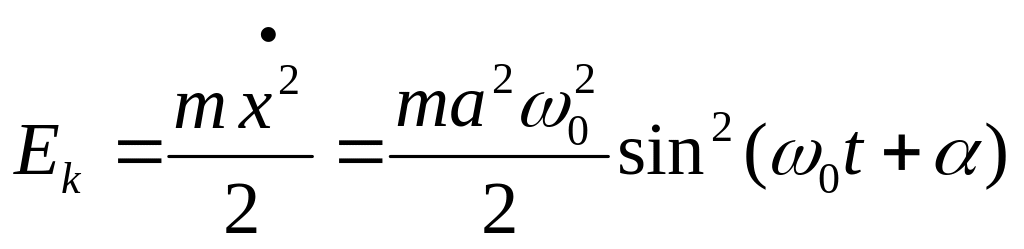, а

Сложив, с учётом , найдем полную энергию колебаний: , т.е., постоянно.

Среднее значение и = , поэтому среднее значение кинетической энергии совпадает со среднем значением потенциальной энергии и равно .

7.3 Математический маятник Это материальная точка, подвешенная на нерастяжимой нити длиною , совершающая колебания в вертикальной плоскости под действием силы тяжести.

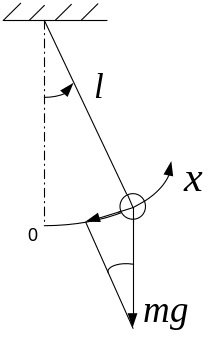
рис.7,5

Записав для пути точки: , а для ускорения , запишем уравнение движения вдоль оси : . Или для малых углов (когда )

.

Таким образом, в этих условиях точка совершает гармонические колебания с частотой и периодом .

7.4. Физический маятник.

Это твердое тело, совершающее колебания вокруг неподвижной оси, связанной с телом. Ось перпендикулярна рисунку и направлена к нам, а момент силы тяжести - от нас. Тогда уравнение движения:

Здесь угловое ускорение , а - расстояние от точки подвеса до центра масс тела С. Для малых колебаний : и тогда:

, т.е., такой маятник также совершает гармонические колебания с частотой и периодом .

Такую же частоту и период имел бы математический маятник с длиной , называемой приведенной.

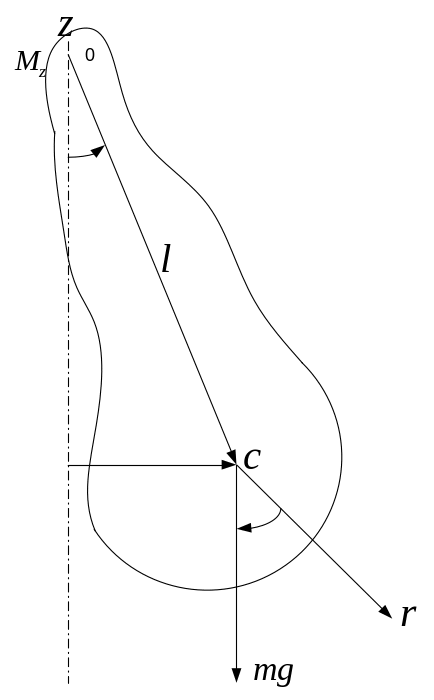
рис.7,6

7.5 Затухающие колебания

В реальной колебательной системе имеются силы сопротивления, действие которых приводят к уменьшению потенциальной энергии системы, и колебания будут затухающими.В простейшем случае сила сопротивления пропорциональна скорости ; r –коэффициент сопротивления. (знак минус, т.к. и имеют противоположные направления )

С учётом 2-ой закон Ньютона имеет вид

или (**)

Это уравнение описывает затухающие колебания системы.

В уравнении затухающих колебаний -частота колебаний, если бы они были свободными, т.е. в отсутствие сил сопротивления. Это собственная частота системы.

Подстановка в диференциальное уравнение приводит к алгебраическому уравнению

с корнями и

При не слишком большом затухании подкоренное выражение будет отрицательным. Представим его в виде , где - вещественная величина .

Общее решение уравнения (**) имеет вид : .

Здесь , т.е., это есть гармонические колебание частоты с амплитудой, меняющейся со временем . Скорость затухания определяется коэффиентом затухания . Период затухающих колебаний ; При небольшом сопротивлении период и растет с ростом .

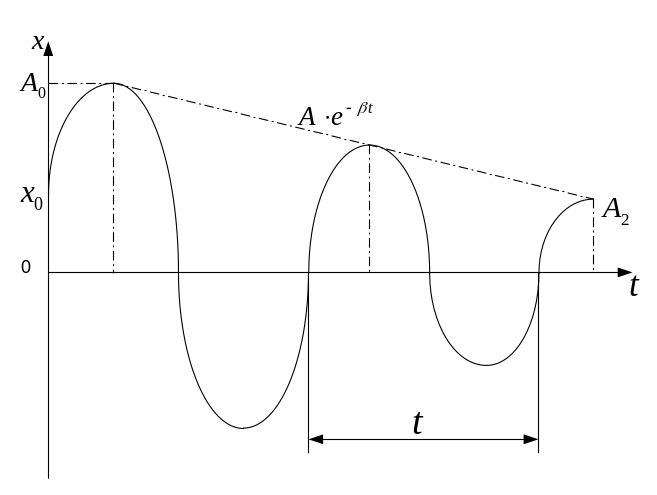
Рис.7,7

Для характеристики скорости затухания колебаний вводят физическую величину – декремент затухания – это отношение амплитуд колебаний, отвечающих моментам времени, отличающимся на период: 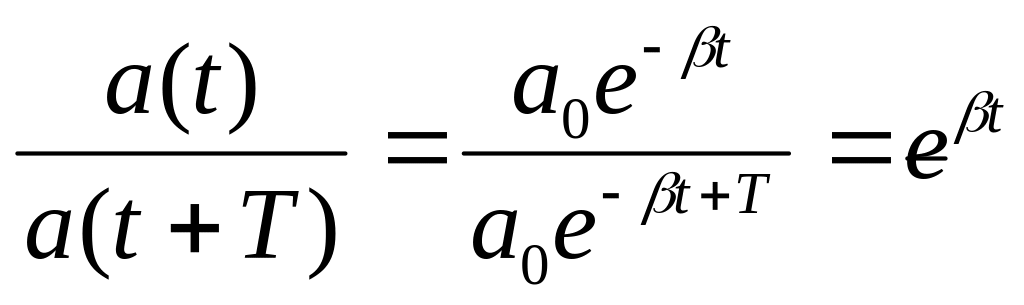, а его логарифм называется логарифмическим декрементом затухания.

Для характеристики колебательной системы обычно используется . Если выразить , то закон убывания амплитуды можно записать:

. Отсюда видно, что за время , за которое амплитуда уменьшается в раз, система успевает совершить колебаний. Из условия : . Т.е., можно сказать, что по величине обратно числу колебаний, совершенных за время , за которое амплитуда уменьшается в раз.

Как техническая характеристика колебаний, часто употребляется добротность: . Другое определение добротности : это отношение энергии колебаний, запасенной в контуре в данный момент, к потерям этой энергии за один период колебаний, умноженной на :

Из формулы для периода колебаний следует, что с ростом коэффициента затухания период увеличивается и при становится равным бесконечности, т.е., колебания прекращаются. При движение носит апериодический характер: система, выведенная из положения равновесия, возвращается в исходное состояние не совершая колебаний одним из двух путей в зависимости от величины начальной скорости, рис. . .

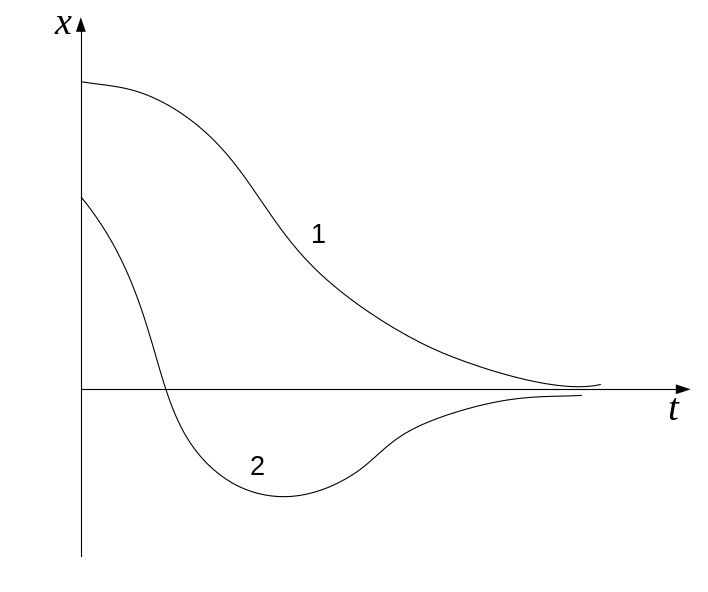
Рис.7,8