
- •12.Линейные операторы. Примеры. Матрица линейного оператора в фиксированном базисе. Действия над линейными операторами.
- •15.Евклидово пространство и тд.
- •16. Метод наименьших квадратов…Системы норм ур-ий.
- •17. Билинейные и квадратичные формы. Сумма квадратов. Лагранж.
- •18 ,19 Итерационные методы решения систем:
- •20.Смешанное произведение трех векторов и его приложения. Необходимое и достаточное условие компланарности трех векторов.
- •21. Уравнение прямой на плоскости, заданной точкой и нормальным вектором.
- •22. Общее уравнение прямой на плоскости. Уравнение прямой в отрезках.
16. Метод наименьших квадратов…Системы норм ур-ий.
Для
произвольного вектора х
= (x1,x2,
... ,хп)T
вектор
δ
= Ах -b
называется
вектором
невязки. х
является
решением системы Ах
=b,
когда вектор невязки равен 0 (или норма
вектора невязки равна нулю).Под
псевдоре-шением системы
Ах
=
b
понимают
любой вектор x,
для которого ||А![]() –b||
достигает
наименьшего значения. Псевдорешение
с наименьшей длиной вектора невязки
называется нормальным
псевдорешением. Оно
всегда существует. Метод
наименьших квадратов основывается
на использовании евклидовой нормы
для
вычисления длины вектора невязки δ,
т.е. минимизируется || δ ||=√ δT
δ. Поскольку система Ах
=b
несовместна,
то b
не
является линейной комбинацией
вектор-столбцов матрицы А.
Норма
вектора невязки ||Аx
–b||
представляет
собой расстояние от b
до
вектора Ах,
лежащего
в пространстве столбцов матрицы А
(так
как Ах
-линейная
комбинация вектор-столбцов матрицы А
с коэффициентами
х1,...,
хп).И
нахождение псевдорешения х
системы
Ах=b
по
методу наименьших квадратов эквивалентно
нахождению вектора р
= А
,
наиболее
близкого к b,
т.е. вектор р
должен
быть проекцией вектора b
на
пространство вектор-столбцов матрицы
А,
и
вектор невязки А
-b
должен
быть ортогонален к этому пространству.
–b||
достигает
наименьшего значения. Псевдорешение
с наименьшей длиной вектора невязки
называется нормальным
псевдорешением. Оно
всегда существует. Метод
наименьших квадратов основывается
на использовании евклидовой нормы
для
вычисления длины вектора невязки δ,
т.е. минимизируется || δ ||=√ δT
δ. Поскольку система Ах
=b
несовместна,
то b
не
является линейной комбинацией
вектор-столбцов матрицы А.
Норма
вектора невязки ||Аx
–b||
представляет
собой расстояние от b
до
вектора Ах,
лежащего
в пространстве столбцов матрицы А
(так
как Ах
-линейная
комбинация вектор-столбцов матрицы А
с коэффициентами
х1,...,
хп).И
нахождение псевдорешения х
системы
Ах=b
по
методу наименьших квадратов эквивалентно
нахождению вектора р
= А
,
наиболее
близкого к b,
т.е. вектор р
должен
быть проекцией вектора b
на
пространство вектор-столбцов матрицы
А,
и
вектор невязки А
-b
должен
быть ортогонален к этому пространству.
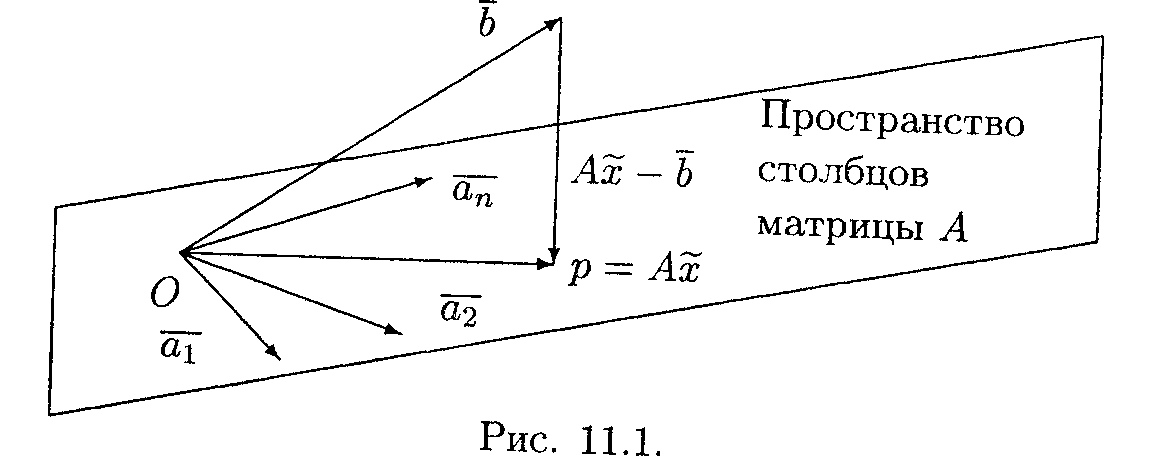
Каждый вектор в пространстве столбцов матрицы А является линейной комбинацией столбцов с некоторыми коэффициентами y1,...,yn т.е. это вектор вида Ау. Для всех у эти векторы на плоскости должны быть перпендикулярны вектору невязки А -b, т.е. (Ау}T(А -b) = 0 или уT(АTА - АТb) = 0. Последнее равенство должно выполняться для произвольного вектора у. Отсюда следует, что АTА -АТb = 0 или АTА = АTb.
Система АTА = АТb носит название системы нормальных уравнений. Если ранг матрицы А равен n, то нормальное псевдорешение является обычным решением квадратной системы нормальных уравнений, т.е. = (АТА)-1АТb.
Для произвольного
вектора
![]() вектор S=Ax-b называется вектором невязки.
Х является решением системы Ax=b, когда
вектор невязки равен 0 (или норма вектора
невязки равна 0). Под псевдорешением
системы Ax=b понимают любой вектор
вектор S=Ax-b называется вектором невязки.
Х является решением системы Ax=b, когда
вектор невязки равен 0 (или норма вектора
невязки равна 0). Под псевдорешением
системы Ax=b понимают любой вектор
![]() ,
для которого
,
для которого
![]() достигает наименьшего значения.
Псевдорешение с наим. длиной вектора
невязки наз-ся нормальным псевдорешением.
Оно всегда существует.
достигает наименьшего значения.
Псевдорешение с наим. длиной вектора
невязки наз-ся нормальным псевдорешением.
Оно всегда существует.
Метод наименьших
квадратов. Основывается
на использовании евклидовой нормы для
вычисления длины вектора невязки S,
т.е. минимизируется
![]() .
.
Нахождение
псевдорешения
системы Ax=b по методу наим. квадратов
эквивалентно нахождению вектора
![]() ,
наиболее близкого к b.
,
наиболее близкого к b.
Каждый вектор в
пространстве столбцов матрицы А явл-ся
линейной комбинацией столбцов с
некоторыми коэффициентами
![]() ,
другими словами, это вектор вида Ay. Для
всех у эти векторы на плоскости должны
быть перпендикулярны вектору невязки
,
другими словами, это вектор вида Ay. Для
всех у эти векторы на плоскости должны
быть перпендикулярны вектору невязки
![]() ,
т.е.
,
т.е.
![]() или
или
![]() .
Последнее равенство должно выполнятся
для произвольного вектора у. Отсюда
следует:
.
Последнее равенство должно выполнятся
для произвольного вектора у. Отсюда
следует:
![]() или
или
![]() .
.
Система наз-ся системой нормальных уравнений.
Если ранг матрицы
равен n, то нормальное псевдорешение
явл-ся обычным решением квадратной
системы нормальных уравнений, т.е.
![]() .
.
