9) Теорема Кронекера-Капелли.
Система
(1) совместна, т.е. имеет хотя бы одно
решение, тогда и только тогда, когда 
,
где
-
расширенная матрица системы (1), причем
1)
если 
,
то система (1) несовместна;
2)
если 
(
-
число неизвестных), то система (1)
неопределенная;
3)
если 
,
то система (1) имеет единственное решение.
У Кронекера эта теорема содержится в его лекциях, читавшихся в Берлинском университете в 1883-1891 г. Капели впервые дал формулировку теоремы с использованием термина «ранг матрицы».
Из сформулированной теоремы вытекает алгоритм решения системы (1):
Пусть 
.
В матрице 
выделяем
базисный минор порядка 
.
С этим минором связаны
уравнений
и
неизвестных
системы (1). Эти уравнения и неизвестные
назовем базисными; все остальные
уравнения системы отбросим, а все
остальные 
неизвестных
в базисных уравнениях перенесем направо.
Получим систему из
базисных
уравнений с
базисными
неизвестными. Т.к. ее определитель,
являясь базисным минором, отличен от
нуля, то по правилу Крамера полученная
система имеет единственное решение.
Это решение, зависящее от
произвольных
постоянных, соответствующих небазисным
неизвестным, и будет решением исходной
системы (1).
Пример. Решить систему
Решение.
,
т.к. все миноры третьего порядка равны
нулю.
,
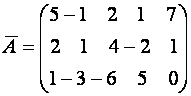
т.к.
,
,
следовательно, система несовместна.
10) Метод Гаусса.
Переходим
к исследованию общих линейных систем.
Рассмотрим систему из 
линейных
уравнений и с
неизвестными:
(3)
Наряду с матрицей составим так называемую расширенную матрицу системы (3) из коэффициентов при неизвестных и правых частей.
Метод Гаусса или метод исключения неизвестных состоит в приведении расширенной матрицы с помощью элементарных преобразований над ее строками к ступенчатому виду:
или 
К элементарным преобразованиям над строками относятся следующие:
1) перемена местами двух строк;
2) умножение строки на число, отличное от нуля;
3) прибавление к строке другой строки, умноженной на произвольное число;
4) выбрасывание нулевой строки.
Расширенной
матрице, приведенной к ступенчатому
виду, соответствует линейная система,
эквивалентная исходной, решение которой
не вызывает затруднения. Реализацию
метода Гаусса рассмотрим на примерах.
Переход от
при
помощи элементарных преобразований
будем обозначать значком эквивалентности 
.
Пример. Решить систему с помощью метода Гаусса.
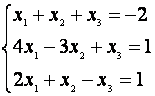
Решение.
Ко второй строке прибавим первую, умноженную на (-4), к третьей – первую, умноженную (-2).
Поменяем местами вторую и третью строки:
К третьей строке прибавим вторую, умноженную на 7:
Полученной ступенчатой матрице соответствует эквивалентная система:
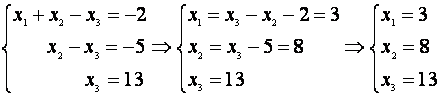
Заключение. Системы линейных алгебраических уравнений играют важную роль при построении математических моделей реальных механических объектов и механических процессов. Рассмотренная в предыдущих лекциях теория матриц позволяет простыми алгебраическими методами исследовать основные вопросы, связанные с системой линейных уравнений: вопрос о ее совместности и вопрос о способах ее решения. Простота этих методов позволяет широко их использовать на ЭВМ.