2.Простейшие дроби

Правильная рациональная алгебраическая дробь Q(x)P(x) называется простейшей, если ее знаменатель Q(x) является натуральной степенью некоторого неприводимого многочлена q(x):

Q(x)=qk(x),(k≥1), 

а степень числителя P(x) меньше степени многочлена q(x). Напомним, что среди многочленов с действительными коэффициентами и со старшим коэффициентом, равным единице, неприводимыми являются лишь линейные многочлены x−c  и квадратные многочлены x2+px+q при условии, что коэффициенты квадратного трехчлена удовлетворяют неравенству p2−4q<0 .

Вследствие этого рациональная алгебраическая дробь может быть простейшей лишь в случаях, когда ее числитель P(x) - либо многочлен первой степени, либо многочлен нулевой степени (т.е. число не равное нулю). Пример. Дробь x−1(x2+1)k (k - натуральное) будет простейшей рациональной алгебраической дробью, так как ее знаменатель является степенью неприводимого многочлена , а степень неприводимого многочлена больше степени числителя.  В теории рациональных алгебраических дробей центральное место занимает следующая теорема: Всякая правильная рациональная дробь разлагается в сумму простейших дробей, и это разложение единственно.

Точнее, если дана правильная дробь Q(x)P(x), знаменатель которой имеет разложение на неприводимые множители: Q(x)=q1k1(x)q2k2(x)...qlkl(x), причем qi(x)/=qj(x)  при i/=j  и k1,k2,...,kl - натуральные числа, то

Q(x)P(x)=p1(x)q1k1(x)+p2(x)q2k2(x)+...+pl(x)qlkl(x),

где все слагаемые в правой части - правильные дроби, каждая из которых может быть представлена в виде суммы простейших дробей:

p(x)qk(x)=qk(x)Sk(x)+qk−1(x)Sk−1(x)+...+q2(x)S2(x)+q(x)S1(x).

Степени всех числителей, стоящих в правой части этого разложения, меньше степени многочлена q(x).

3. Разложение правильной рациональной дроби на простейшие

Пусть знаменатель правильной рациональной дроби   может быть представлен в виде   (множителей вида  может быть несколько), где  — заданные числа

 трехчлен не имеет действительных корней.

Тогда представляется в виде суммы простейших дробей

1—3 типов:

 

где — неизвестные коэффициенты, которые находятся путем приведения суммы справа к общему знаменателю и последующего приравнивания полученного числителя к Доказательство представлено в [3. С.354].

Примеры:

1)

2)

3)

Два метода нахождения коэффициентов в разложении рассмотрим на примере.

Пример:

Поскольку (см. пример в

п. 16.1.1), то

Правильную рациональную дробь под интегралом представим в виде суммы простейших:

 (16.1)

Первый метод — метод неопределенных коэффициентов — заключается в приравнивании коэффициентов при одинаковых степенях х в (16.1):

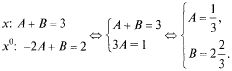
Второй метод — метод частных значений — заключается в подстановке значений х в (16.1), в первую очередь, корней знаменателя:

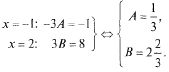
Окончательно имеем

4. Метод неопределенных коэффициентов

Рассмотрим два многочлена   степени   и   соответственно, т.е.

предположим, что   .

При делении многочлена   на многочлен   , где   , нужно найти многочлены  и   такие, чтобы выполнялось равенство

Опишем метод неопределенных коэффициентов. Этот метод основывается на том, что многочлен   -ой степени имеет ровно   корней с учетом их кратности. Это означает, что если многочлен обращается в нуль более чем в   точках, то этот многочлен нулевой (все коэффициенты равны нулю).

Запишем многочлены   и   с произвольными коэффициентами, т.е.

и

Умножим и сложим многочлены в левой части равенства:

получим

здесь приведены подобные, т.е. группировка по степеням   .

В итоге получим, что для любого значения переменной   выполняется равенство левой и правой частей. Это означает, что многочлен   -ой степени обращается в нуль более, чем в  точках. Для равенства нулю многочлена достаточно потребовать равенства нулю всех его коэффициентов.

Приравняем друг к другу коэффициенты при одинаковых степенях   в равенстве

или

Имеем систему линейных алгебраических уравнений:

из которой определяются неизвестные коэффициенты.