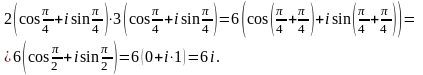- •Элементы линейной алгебры
- •1)Матрицы и операции над ними
- •Основные действия над матрицами
- •Транспонирование матриц
- •Обратная матрица
- •Вычислительная сложность
- •Свойства обратной матрицы
- •Способы нахождения обратной матрицы
- •Точные (прямые) методы Метод Гаусса—Жордана
- •С помощью матрицы алгебраических дополнений
- •Использование lu/lup-разложения
- •Примеры Матрица 2х2
- •8) Ранг матрицы
- •9) Теорема Кронекера-Капелли.
- •10) Метод Гаусса.
- •2. Векторная алгебра и аналитическая геометрия в пространстве
- •1) Линейные операции над векторами
- •2) Проекция вектора на ось, свойства проекции
- •4) Деление отрезка в данном отношении
- •11) Угол между плоскостями. Условия параллельности и перпендикулярности плоскостей.
- •12) Параметрические уравнения прямой
- •13) Угол между прямыми
- •14) Угол между прямой и плоскостью
- •1)Комплексные числа. Модуль и аргумент.
- •Комплексные равенства (Сформулируйте смысл комплексного равенства)
- •Геометрическое изображение комплексных чисел (в чём состоит геометрическое изображение комплексных чисел?)
- •Модуль и аргумент комплексного числа (Что такое модуль и аргумент комплексного числа?)
- •2)Алгебраическая и тригонометрическая формы комплексного числа (Что такое алгебраическая и тригонометрическая формы комплексного числа?)
- •Основные свойства умножения
- •Деление комплексных чисел
- •Возведение комплексного числа в натуральную степень
- •Извлечение корня натуральной степени из комплексного числа
- •4)Формулы Эйлера. Формула Муавра
- •Рациональные функции
- •1.Рациональные дроби. Теорема Безу
- •2.Простейшие дроби
- •3. Разложение правильной рациональной дроби на простейшие
- •4. Метод неопределенных коэффициентов
1)Комплексные числа. Модуль и аргумент.
Комплексным числом z называется выражение следующего вида:
![]() Комплексное
число в алгебраической форме,(1)
Комплексное
число в алгебраической форме,(1)
Где x, y ;
i — это мнимая единица, определяемая равенством i2 = –1.
Основные термины:
x = Re z — действительная часть комплексного числа z;
y = Im z — мнимая часть комплексного числа z;
 — комплексно
сопряженное число
числу
z;
— комплексно
сопряженное число
числу
z;
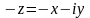 — противоположное
число
числу
z;
— противоположное
число
числу
z;
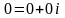 — комплексный
ноль;
— комплексный
ноль;
 – так обозначается
множество комплексных чисел.
– так обозначается
множество комплексных чисел.
Примеры
1)z = 1 + i
Re z = 1,
Im z = 1,
 = 1 – i,
= 1 – i,
 = –1 – i;
= –1 – i;
2)z = –1 +  i
Re z = –1,
Im z =
,
= –1 –
i,
= –1 –
i;
i
Re z = –1,
Im z =
,
= –1 –
i,
= –1 –
i;
3)z = 5 + 0i = 5 Re z = 5, Im z = 0, = 5 – 0i = 5, = –5 – 0i = –5
если Im z = 0, то z = x — действительное число;
4)z = 0 + 3i = 3i Re z = 0, Im z = 3, = 0 – 3i = –3i, = –0 – 3i = – 3i
если Re z = 0, то z = iy — чисто мнимое число.
Комплексные равенства (Сформулируйте смысл комплексного равенства)
1)
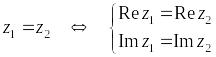 ;
;
2)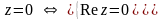 .
.
Одно комплексное равенство равносильно системе двух действительных равенств. Эти действительные равенства получаются из комплексного равенства разделением действительных и мнимых частей.
Примеры
1)
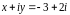
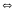
 ;
;
2)
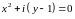
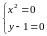
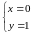 .
.
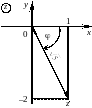
Геометрическое изображение комплексных чисел (в чём состоит геометрическое изображение комплексных чисел?)
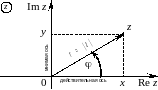
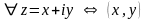
Комплексное число z изображается точкой (x, y) на комплексной плоскости или радиус-вектором этой точки.
З нак
z
во
второй четверти означает, что система
декартовых координат
нак
z
во
второй четверти означает, что система
декартовых координат
 будет использоваться как комплексная
плоскость.
будет использоваться как комплексная
плоскость.
Модуль и аргумент комплексного числа (Что такое модуль и аргумент комплексного числа?)
Модулем
комплексного числа
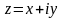 называется неотрицательное действительное
число
называется неотрицательное действительное
число
 .(2)
.(2)
Геометрически модуль комплексного числа — это длина вектора, изображающего число z, или полярный радиус точки (x, y).
Аргумент комплексного числа z — это угол между положительным направлением действительной оси и вектором z (геометрически – это полярный угол точки (x, y)).
Обозначение
 ,
причем
,
причем
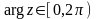 ,
или
,
или
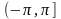 .
.
Для вычисления аргумента комплексного числа используется формула
![]() Аргумент
комплексного числа
,(3)
Аргумент
комплексного числа
,(3)
причем,
при определении угла
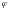 по его тангенсу обязательно нужно
учитывать, в какой четверти на комплексной
плоскости расположено число z:
по его тангенсу обязательно нужно
учитывать, в какой четверти на комплексной
плоскости расположено число z:
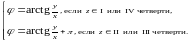
2)Алгебраическая и тригонометрическая формы комплексного числа (Что такое алгебраическая и тригонометрическая формы комплексного числа?)
Так
как геометрически очевидно, что
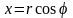 и
и
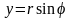 ,
то
,
то
![]() Тригонометрическая
форма комплексного числа
.(4)
Тригонометрическая
форма комплексного числа
.(4)
Запись z = x + iy называется алгебраической формой комплексного числа z; запись z = r(cos + i sin) называется тригонометрической формой комплексного числа z.
Примеры
Изобразить на комплексной плоскости следующие числа и записать их в тригонометрической форме.
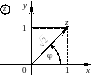
1)z = 1 + i
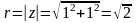 ,
,
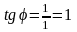
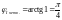
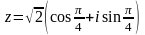 ;
;
2)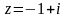
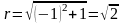 ,
,
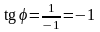
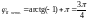
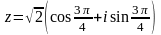 ;
;
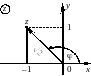
3)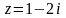
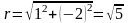 ,
,

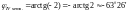
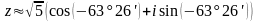 ;
;
4)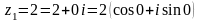 ,
,
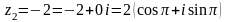 ;
;
5) ,
,
 ;
;

6) ,
,
то есть для z = 0 будет
 ,
не определен.
,
не определен.
3)Арифметические действия над комплексными числами (Дайте определения и перечислите основные свойства арифметических действий над комплексными числами.)
Сложение (вычитание) комплексных чисел
z1 z2 = (x1 + iy1) (x2 + iy2) = (x1 x2) + i(y1 y2),(5)
то есть при сложении (вычитании) комплексных чисел складываются (вычитаются) их действительные и мнимые части.
Примеры
1)(1 + i) + (2 – 3i) = 1 + i + 2 –3i = 3 – 2i;
2)(1 + 2i) – (2 – 5i) = 1 + 2i – 2 + 5i = –1 + 7i.
Основные свойства сложения
1)z1 + z2 = z2 + z1;
2)z1 + z2 + z3 = (z1 + z2) + z3 = z1 + (z2 + z3);
3)z1 – z2 = z1 + (– z2);
4)z + (–z) = 0;
5)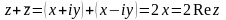 .
.
Умножение комплексных чисел в алгебраической форме
z1∙z2 = (x1 + iy1)∙(x2 + iy2) = x1x2 + x1iy2 + iy1x2 + i2y1y2 = (6)
= (x1x2 – y1y2) + i(x1y2 + y1x2),
то есть
умножение комплексных чисел в
алгебраической форме проводится по
правилу алгебраического умножения
двучлена на двучлен с последующей
заменой
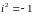 и приведением подобных по действительным
и мнимым слагаемым.
и приведением подобных по действительным
и мнимым слагаемым.
Примеры
1)(1 + i)∙(2 – 3i) = 2 – 3i + 2i – 3i2 = 2 – 3i + 2i + 3 = 5 – i;
2)(1 + 4i)∙(1 – 4i) = 1 – 42 i2 = 1 + 16 = 17;
3)(2 + i)2 = 22 + 4i + i2 = 3 + 4i.
Умножение комплексных чисел тригонометрической форме
z1∙z2 = r1(cos1 + isin1)r2(cos2 + isin2) =
= r1r2(cos1cos2 + icos1sin2 + isin1cos2 + i2 sin1sin2) =
= r1r2((cos1cos2 – sin1sin2) + i(cos1sin2 + sin1cos2))
![]()
Произведение комплексных чисел в тригонометрической форме , то есть при умножении комплексных чисел в тригонометрической форме их модули перемножаются, а аргументы складываются.
Пример