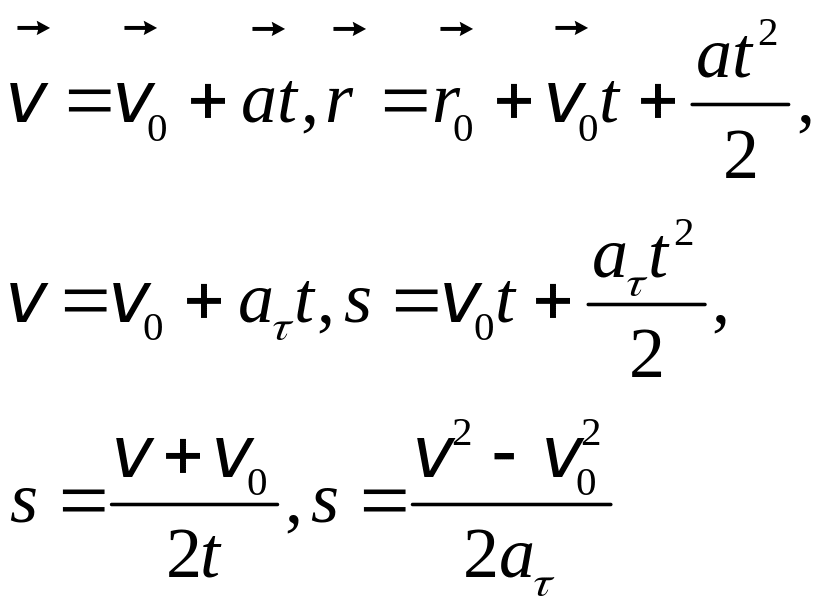- •Механика
- •Молекулярная физика
- •Равномерное движение
- •Равномерное прямолинейное движение
- •1.5.3. Движение по произвольной траектории с постоянной тангенциальной составляющей вектора ускорения aτ.
- •Равноускоренное движение с изменяющейся тангенциальной составляющей ускорения
- •Прямолинейное равноускоренное движение
- •Виды движения твердого тела
- •4. Виды сил в механике. Силы упругости (закон Гука), трения, сопротивления среды. Сила тяжести и вес.
- •Замкнутая система тел. Закон сохранения импульса. Центр инерции механической системы и закон его движения. Движение тела переменной массы.
- •6.Законы Ньютона в неинерциальных системах отсчета. Силы инерции. Центробежная сила инерции, и ее влияние на вес тела на Земле. Сила Кориолиса. Принцип эквивалентности Эйнштейна.
- •Работа в механике. Работа постоянной и переменной сил. Графическое представление работы. Мощность.
- •8.Механическая энергия и ее виды. Кинетическая энергия и работа равнодействующей силы. Закон сохранения механической энергии.
- •Столкновение тел. Удар. Законы сохранения импульса и энергии при упругом и неупругом ударах. Вычисление скоростей соударяющихся тел. Потери механической энергии при неупругом ударе.
- •1 1.Момент инерции материальной точки и твердого тела. Вычисление момента инерции однородного диска. Теорема Штейнера. Свободные и главные оси вращения. Основной закон динамики вращательного движения.
- •Момент силы относительно точки и оси. Момент пары сил. Основной закон динамики вращательного движения.
- •Работа, совершаемая при вращении тела. Кинетическая энергия вращения. Сравнительный расчет скоростей центра масс шара и диска, скатывающихся с наклонной плоскости.
- •15. Колебательное движение. Виды колебаний. Гармонические колебания. Их уравнение, график, характеристики. Скорость, ускорение и энергия при гармонических колебаниях.
- •17.Затухающие колебания. Их уравнение, график и основные характеристики.
- •Вынужденные колебания. Резонанс.
- •Внешняя сила
- •Квазиупругая сила
- •Маятники. Уравнение движения физического маятника. Математический маятник. Приведенная длина физического маятника.
- •20.Волновой процесс, основное свойство волн. Упругие волны. Волновая поверхность и волновой фронт. Продольные и поперечные волны. Уравнение плоской и сферической бегущих волн. Волновое уравнение.
- •2 1.Уравнение плоской бегущей волны. Перенос энергии волной. Вектор Умова. Интенсивность волны. Затухающие волны.
- •22. Интерференция плоских волн. Стоячие волны. Расчет координат узлов и пучностей. Колебания струны
- •23. Суперпозиция волн близкой частоты. Волновой пакет. Групповая скорость волн. Дисперсия волн.
- •24. Звуковые волны. Эффект Доплера в акустике.
- •1 Моль — это количество вещества, в котором содержится столько же атомов, сколько их в 12 г углерода .
- •6. Адиабатический процесс. Первое начало термодинамики для адиабатического процесса. Политропные процессы.
- •Работа газа при изменении объема. Расчет работы, совершаемой газом в различных изопроцессах.
- •Работа моля газа при нагревании на 1 к
- •Столкновения молекул. Эффективный диаметр молекул, средняя длина свободного пробега.
- •10.Круговые процессы (циклы). Работа в круговом процессе. Тепловые и холодильные машины. Цикл Карно.
- •11.Явления переноса в термодинамически неравновесных системах. Вычисление коэффициентов теплопроводности, диффузии и внутреннего трения.
- •12.Взаимодействие молекул. Реальные газы. Уравнение Ван-дер-Ваальса. Изотермы Ван-дер-Ваальса и их анализ. Внутренняя энергия реального газа.
- •13. Поверхностное натяжение жидкостей. Давление под искривленной поверхностью. Смачивание. Капиллярные явления.
- •14. Ламинарное и турбулентное течение жидкости. Уравнение неразрывности струи. Уравнение Бернулли. Внутреннее трение. Движение тел в жидкостях и газах.
- •Твердые тела. Типы кристаллических твердых тел. Фазовые переходы в твердых телах. Диаграмма состояния. Тройная точка.
Равноускоренное движение с изменяющейся тангенциальной составляющей ускорения
Движение называют
равноускоренным, если оно происходит
с постоянным вектором полного ускорения
![]() const.
Если тангенциальная составляющая
ускорения при этом не остаётся постоянной,
то формулы для скорости и пути, полученные
в предыдущем параграфе, не будут
справедливы.
const.
Если тангенциальная составляющая
ускорения при этом не остаётся постоянной,
то формулы для скорости и пути, полученные
в предыдущем параграфе, не будут
справедливы.
Примером такого движения может служить движение тела в однородном поле тяготения Земли или движение заряженной частицы в однородном электрическом поле плоского конденсатора.
На рисунке 1.14 показана траектория движения камня, брошенного под углом к горизонту в поле тяготения Земли. Выберем оси координат таким образом, чтобы вектор скорости при движении тела лежал в плоскости xy.
В
Рис. 1.14. о
всех точках траектории камень обладает
постоянным полным ускорением
о
всех точках траектории камень обладает
постоянным полным ускорением
![]() ,
равным ускорению свободного падения
,
равным ускорению свободного падения
![]() ,
а нормальная и тангенциальная составляющие
полного ускорения не остаются постоянными.
В точке А
векторы
,
а нормальная и тангенциальная составляющие
полного ускорения не остаются постоянными.
В точке А
векторы
![]() и
направлены противоположно, проекция
вектора тангенциального ускорения на
направление скорости отрицательна,
и
направлены противоположно, проекция
вектора тангенциального ускорения на
направление скорости отрицательна,![]() .
В точке В
.
В точке В
![]() ,
в точке С
,
в точке С
![]() .
.
Определим зависимость
вектора скорости от времени наблюдения.
Исходя из определения вектора полного
ускорения
![]() ,
запишем элементарное изменение вектора
скорости как
,
запишем элементарное изменение вектора
скорости как![]() .
Интегрируя, получим
.
Интегрируя, получим![]() .
Константу интегрирования С
определим из начальных условий: пусть
в начале наблюдения при t
= 0 материальная точка имела скорость
.
Константу интегрирования С
определим из начальных условий: пусть
в начале наблюдения при t
= 0 материальная точка имела скорость
![]() ,
тогда
,
а зависимость вектора скорости от
времени принимает вид
,
тогда
,
а зависимость вектора скорости от
времени принимает вид
![]()
Проецируя каждый вектор на оси координат, получим
![]() ,
,
тогда модуль
скорости![]() .
.
Аналогично определим
зависимость радиус-вектора
материальной точки от времени наблюдения.
Из определения вектора скорости
![]() запишем элементарное изменение
радиус-вектора как
запишем элементарное изменение
радиус-вектора как
![]() .
Интегрируя, получим
.
Интегрируя, получим![]() ,
и
,
и
![]() .
Константу интегрирования определим из
начальных условий: пусть в начальный
момент отсчета времени t
= 0 материальная
точка имела радиус-вектор
.
Константу интегрирования определим из
начальных условий: пусть в начальный
момент отсчета времени t
= 0 материальная
точка имела радиус-вектор![]() ,
тогдa
,
а зависимость радиус-вектора от времени
принимает вид
,
тогдa
,
а зависимость радиус-вектора от времени
принимает вид
![]() .
(1.5)
.
(1.5)
Если
в момент времени t
= 0 радиус-вектор
![]() (точка начинает движение из начала
координат), тогда
(точка начинает движение из начала
координат), тогда
![]() .
.
Для определения положения материальной точки в любой момент времени спроецируем каждый вектор, входящий в уравнение (1.5), на оси координат:
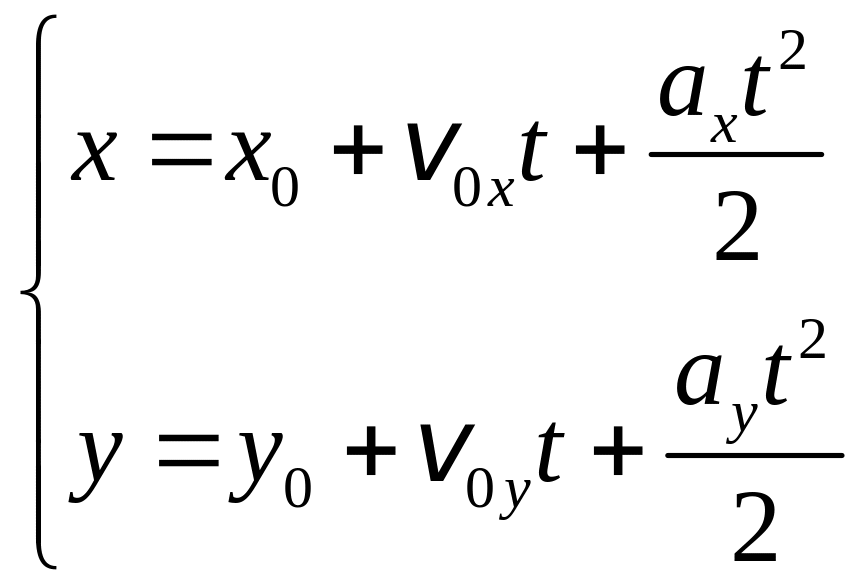 ,
(1.6)
,
(1.6)
где
координата
![]() есть
проекция радиус-вектора на ось Ох,
координата
есть
проекция радиус-вектора на ось Ох,
координата
![]() –
проекция радиус-вектора на ось Оу.
–
проекция радиус-вектора на ось Оу.
При движении тела
в поле силы тяжести горизонтальная
составляющая полного ускорения
отсутствует, горизонтальная компонента
скорости постоянна (![]() ,
,![]() const.),
следовательно, координата х
вычисляется
по формуле равномерного движения:
const.),
следовательно, координата х
вычисляется
по формуле равномерного движения:
![]() .
.
Вертикальная
составляющая ускорения
![]() (
– ускорение свободного падения), и
координата у
вычисляется по формуле (1.6).
(
– ускорение свободного падения), и
координата у
вычисляется по формуле (1.6).
Прямолинейное равноускоренное движение
В случае прямолинейного
движения радиус кривизны траектории
R
стремится к бесконечности, и материальная
точка не обладает нормальным ускорением
(![]() ).
Вектор полного ускорения в этом случае
представлен только тангенциальной
компонентой (
).
Вектор полного ускорения в этом случае
представлен только тангенциальной
компонентой (![]() )
и направлен вдоль траектории движения.
Если вектор ускорения сонаправлен с
вектором скорости, то в этом случае
модуль скорости возрастает, и такое
движение называют прямолинейным
равноускоренным
движением.
Если вектор ускорения имеет направление
противоположное вектору скорости, то
в этом случае модуль скорости убывает,
и такое движение называют прямолинейным
равнозамедленным
движением.
Так как при этом виде движения и
)
и направлен вдоль траектории движения.
Если вектор ускорения сонаправлен с
вектором скорости, то в этом случае
модуль скорости возрастает, и такое
движение называют прямолинейным
равноускоренным
движением.
Если вектор ускорения имеет направление
противоположное вектору скорости, то
в этом случае модуль скорости убывает,
и такое движение называют прямолинейным
равнозамедленным
движением.
Так как при этом виде движения и
![]() ,
и
,
и
![]() ,
то все соотношения, выведенные в двух
предыдущих параграфах, будут справедливы:
,
то все соотношения, выведенные в двух
предыдущих параграфах, будут справедливы: