6. Адиабатический процесс. Первое начало термодинамики для адиабатического процесса. Политропные процессы.

А диабатический процесс происходит без теплообмена с внешней средой.

Г аз совершает работу за счет своей внутренней энергии. При адиабатическом расширении он охлаждается, при сжатии – нагревается.

Уравнение Пуассона для адиабатического процесса

Политропный процесс – термодинамический процесс, во время которого удельная теплоемкость (С) газа остается неизменной. Предельными частными явлениями политропного процесса являются адиабатический и изотермический процессы. В случае идеального газа изобарный и изохорный процессы также являются политропными.

7. Работа газа при изменении объема. Расчет работы, совершаемой газом в различных изопроцессах.

Изотермический. Т.к. то внутренняя энергия газа не изменяется

И зохорный

И

Работа моля газа при нагревании на 1 к

зобарный

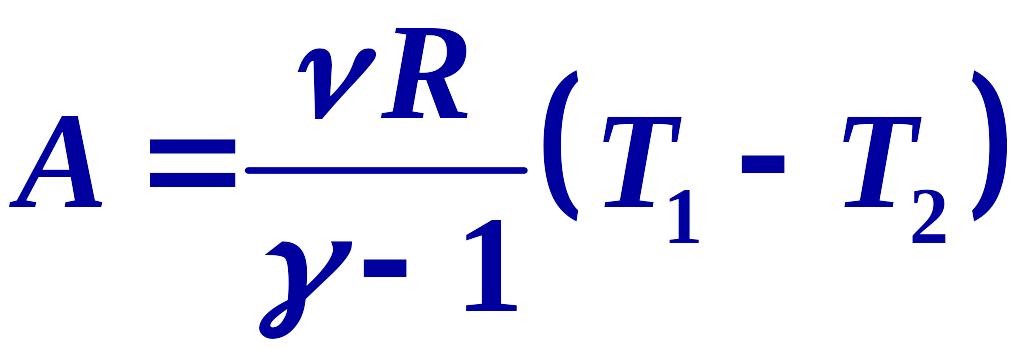
Адиабатический

Работа газа при изменении объема dA=pdV

7. Столкновения молекул. Эффективный диаметр молекул, средняя длина свободного пробега.

Молекулы газа сталкиваются друг с другом.

Р асстояние, которое молекула в среднем проходит между двумя последующими соударениями, называют средней длиной свободного пробега .

Э ффективный диаметр молекул – это кратчайшее расстояние, на которое они сближаются при столкновении.

Средний путь за 1 сек./ среднее число ударов за 1 сек.

9. Макро- и микросостояния. Понятие статистического веса (термодинамической вероятности). Равновесное макросостояние, флуктуации параметров состояния. Обратимые и необратимые процессы. Энтропия и ее свойства. Второе начало термодинамики. Статистический смысл энтропии. Гипотеза Приведенная теплота. Вычисление энтропии. Теорема Нернста. Вечные двигатели I-го и II-го рода.

Макросостояние – это состояние, заданное с помощью величин, характеризующих всю систему в целом (p, V, T).

М икросостояние – это состояние, заданное с помощью координат и импульсов всех молекул.

Число микросостояний , соответст-вующих данному макросостоянию, называют термодинамической вероятностью или статистическим весом этого макросостояния.

Р авновесному макросостоянию соответ-ствует наибольшая термодинамическая вероятность:

Система может испытывать небольшие отклонения от равновесного состояния. Их называют флуктуациями.

Обратимый процесс может происходить как в прямом, так и в обратном направлении через те же промежуточные состояния. Если система вернулась в исходное состояние, ни в ней, ни в окружающей среде не возникает никаких изменений. Обратимый процесс протекает через равновероятные состояния.

Необратимые процессы протекают только в одном направлении. Обратные им процессы маловероятны. Например, расширение газа в пустоту.

В еличину S=kln называют энтропией.

Энтропия характеризует степень молекулярного беспорядка.

У порядоченные состояния реализуются малым числом способов – энтропия мала. Неупорядоченные состояния реализуются большим числом способов – энтропия велика.

Второе начало термодинамики В изолированной системе энтропия не убывает.

О на увеличивается при необратимом процессе и остается неизменной при обратимом процессе.

В ычисление энтропии Отношение называют приведенной теплотой.

В обратимом процессе

Т еорема Нернста

Следствие:

1. Любая теплоемкость системы при T стремится к 0 стремится к нулю.

2. Абсолютный нуль температуры недостижим.

Вечный двигатель первого рода – устройство, способное бесконечно совершать работу без затрат топлива и других энергетических ресурсов. По ЗСЭ его изобретение невозможно. Также невозможность его осуществления постулируется в первом начале термодинамики

Вечный двигатель второго рода – машина, которая будучи пущена в ход, превращала бы работу в тепло, извлекаемое из окружающих тел. Невозможность его осуществления постулируется во втором начале термодинамики в качестве одной из эквивалентных формулировок.