17. Процессы авторегрессии
Существуют модели образования случайных стационарных сигналов, в которых наиболее существенные свойства временной последовательности заключены в математико-вероятностной структуре. Наиболее простой и часто используемой моделью такого рода является модель процесса авторегрессии (модель АР), которая описывается стохастическим разностным уравнением вида
,
(9)
где предполагается,
что случайные величины
имеют одинаковые и независимые
распределения, нулевое математическое
ожидание, а также общую дисперсию
(т.е. являются отсчетами белого шума).
Величина
по-прежнему обозначает среднее
(матожидание) сигнала
.
Следует уточнить, что процесс авторегрессии,
задаваемый соотношением (9), называется
процессом
авторегрессии М-ого порядка.
18. Ковариационная и корреляционная матрицы случайного процесса, автоковариационная и автокорреляционная функции
Анализ процессов в большинстве случаев выполняется в предположении, что независимая повторная выборка сигнала не может быть получена. Поэтому все оценки, полученные по единственной реализации , «зависящей» от времени, предполагаются идентичными оценкам, которые можно было бы получить по ансамблю реализаций.
Из
предположения о стационарности процесса,
порождающего сигнал, следует, что
совместное распределение вероятностей
величин
и
одинаково для всех времен
и
,
разделенных одним и тем же сдвигом
времени
.
Для эквидистантных сигналов сдвиг между
и
обычно характеризуется разностью
индексов
временных точек
и
,
которая
называется задержкой
или сдвигом;
для наблюдений
и
сдвиг равен k.
Ковариация между значениями
и
,
отделенными k
равными интервалами времени, называется
автоковариацией
с
задержкой
k
и определяется как
. (3.1)
Очевидно, дисперсия
величины
равна C(0),
и, поскольку она не зависит от времени
(во всех точках
дисперсия стационарного процесса
одинакова),
можно записать
.
Автокорреляция
со сдвигом k
равна
, (3.2)
откуда вытекает, что
и
для k
=1, 2, …
Отметим, что,
согласно определению, автоковариации
и автокорреляции могут быть заданы и
для отрицательных сдвигов, причем
формула (3.1) показывает, что
(3.3)
и, следовательно,
. (3.4)
Ковариационная
матрица,
связанная с процессом, для наблюдений
,
где
и
,
имеет вид
=
=
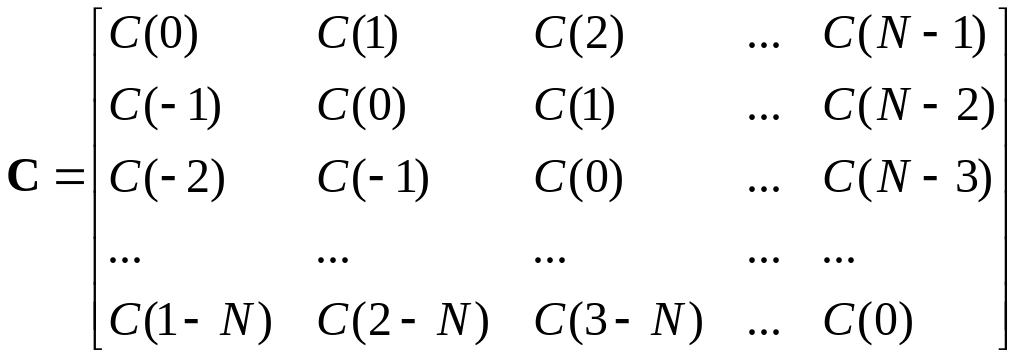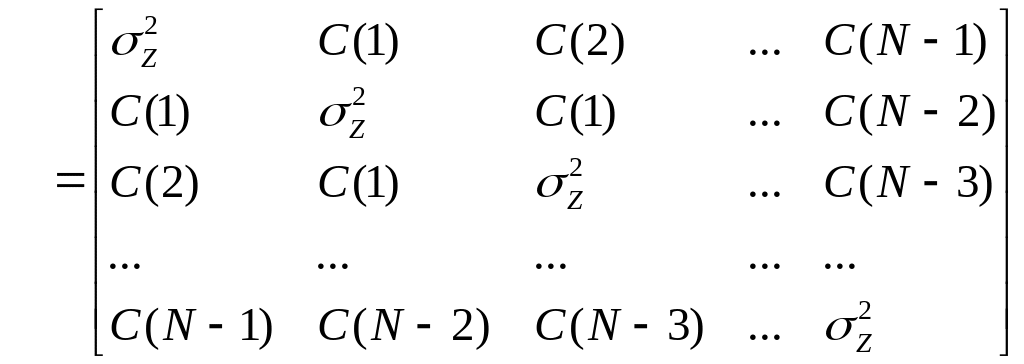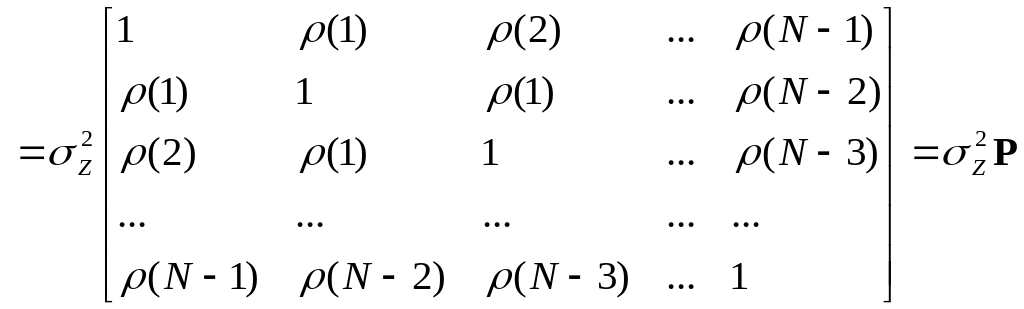. (3.5)
Ковариационная
матрица
такого вида (симметричная и с одними и
теми же элементами на любой диагонали)
называется автоковариационной
матрицей;
соответствующая корреляционная матрица
называется автокорреляционной
матрицей.
Матрицы
и
являются положительно определенными
(определитель и все главные миноры
каждой из этих матриц положительны).
Функция C(k)
от задержки k
называется автоковариационной
функцией
соответствующего процесса. Аналогично
функция
от задержки k
называется автокорреляционной
функцией.
Заметим, что автокорреляционная функция
безразмерна, т. е. независима от
масштаба измерения сигнала. Так как
,
знание автокорреляционной функции
и дисперсии
эквивалентно знанию автоковариационной
функции
.
На рисунках 3.1 и 3.2 показаны правые (для
неотрицательных сдвигов) половины двух
различных автокорреляционных функций.
Из рисунков видно, что автокорреляционные
функции характеризуются тенденцией к
затуханию по мере роста сдвига k.
Такие автокорреляционные функции часто
встречаются на практике. В дальнейшем,
когда будем говорить об автокорреляционной
функции, мы будем иметь в виду ее правую
половину.
Положительное
значение корреляции
свидетельствует о положительной
статистической зависимости между
отсчетами ряда, разделенными интервалом
,
где
интервал дискретизации процесса по
времени. Положительное значение
(
)
означает, что при превышении отсчетом
математического ожидания
,
наиболее вероятным будет исход, при
котором значение
также будет больше, чем
,
а если
,
то значение
будет меньше, чем
,
для большинства индексов n.
При отрицательной корреляции (
)
разности
и
будут иметь в основном различные знаки.