
- •1. Основные определения: информация, сообщение, система связи, сигнал, алфавит.
- •2. Функциональная система цифровой системы связи.
- •3. Преимущества и недостатки цифровой связи
- •4.Четырехуровневая коммуникационная система
- •5. Эталонная модель (osi): стек протоколов
- •6. Уровни модели взаимодействия открытых систем osi
- •Блочная диаграмма типичной системы цифровой связи от источника к передатчику
- •Блочная диаграмма типичной системы цифровой связи от приемника к потребителю информации
- •9. Отображение цифрового сигнала в виде аналоговой функции времени
- •10. Сигнал как реализация процесса. Классификация процессов
- •12. Полигармонические и почти периодические процессы
- •13. Определение случайного процесса
- •14. Процесс стационарный в широком смысле
- •15. Процесс стационарный в узком смысле
- •16. Случайные эргодические процессы, гауссов процесс
- •17. Процессы авторегрессии
- •18. Ковариационная и корреляционная матрицы случайного процесса, автоковариационная и автокорреляционная функции
- •19. Оценивание ковариационной и корреляционной матриц случайного процесса и автоковариационной и автокорреляционной функций
- •20. Случайные нестационарные процессы, характеристики случайных процессов
- •21. Классификация шумов в системах связи.
- •22. Определение спектральной плотности мощности. Теорема Винера-Хинчина.
- •23. Непрерывное преобразования Фурье
- •24. Финитное преобразование Фурье
- •25. Дискретное преобразование Фурье (дпф).
- •26. Свойства дпф.
- •27. Оценивание спектральной плотности с помощью дпф
- •28. Модель белого шума.
- •29. Линейные системы с постоянными параметрами.
- •Характеристики линейных систем с постоянными параметрами.
- •31. Последовательное включение систем с постоянными параметрами.
- •32. Связь спектральных плотностей входного и выходного процессов линейной системы с постоянными параметрами.
- •3 5. Узкополосные и широкополосные сигналы.
- •36. Критерии определения ширины полосы.
- •Форматирование текстовой информации в системах dcs.
- •38. Теорема о дискретном представлении. Критерий Найквиста. Инженерный критерий Найквиста.
- •Дискретизация с помощью идеальных единичных импульсов (идеальная дискретизация).
- •Естественная дискретизация.
- •41.Дискретизация по методу «выборка-хранение».
- •42.Квантование амплитуды и характеристики.
- •45.Шум квантования.
- •46.Импульсно кодовая модуляция квантованных выборок аналогового сигнала.
- •47.Кодирование источников определения.
- •48.Дискретные источники и их характеристики.
- •49.Типы дискретных источников.
- •50.Свойства кодов.
- •51. Показатели кодирования
- •52. Кодирование источников без памяти: код шеннона-фано
- •54. Кодирование источников с памятью: методы подавления нулей и групповое кодирование
- •55. Кодирование источников с памятью: методы подстановки образцов и дифференциальное сжатие
- •56. Униполярные и биполярные сигналы pcm
- •57. Сигналы рсм в кодировке nrz (nrz-l, nrz-m, nrz-s)
- •58. Кодировки nrz-ami и rz-ami
- •59. Фазовое кодирование
- •60. Кодирование модуляцией задержки
- •61. Многоуровневое кодирование рсм. Достоинства и недостатки
- •62. Искажение сигналов шумом awgn
- •63. Межсимвольная интерференция
- •64. Обобщенная схема передачи узкополосного сигнала
- •65. Основные этапы демодуляции/обнаружения
- •68. Униполярная передача двоичных сигналов
- •69. Биполярная передача двоичных сигналов
- •70. Эквивалентная модель системы dcs
- •71. Импульсы Найквиста
- •72. Компенсация искажений с помощью выравнивания
- •73. Виды выравнивания и типы эквалайзеров.
- •74. Дискретный канал без памяти
- •75. Теорема кодирования канала
- •76. Теорема о пропускной способности канала
- •Зачем нужна широкополосная модуляция?
- •78, 79. Амплитудная и частотная модуляция (ask и fsk)
- •80. Частотная манипуляция и бинарная частотная манипуляция
- •81. Бинарная фазовая манипуляция, квадратурная фазовая манипуляция
- •82. Амплитудно-фазовая манипуляция (арк)
- •83. Определение полосовой демодуляции и ее виды
- •84. Ресурс связи и способы его распределения
- •85. Сигналы, ортогональные во времени и по частоте
- •86. Уплотнение/множественный доступ с частотным разделением
- •87. Множественный доступ с временным разделением
14. Процесс стационарный в широком смысле
Если физическое
явление описывается случайным процессом,
то свойство этого явления в принципе
можно оценить в любой момент времени
путем усреднения по ансамблю выборочных
функций
![]() ,
образующих случайный процесс. Тогда
математическое
ожидание
случайного процесса в момент времени
,
образующих случайный процесс. Тогда
математическое
ожидание
случайного процесса в момент времени
![]() можно вычислить, взяв мгновенные
значения всех выборочных функций
ансамбля в момент времени
,
сложив эти значения и разделив на число
слагаемых, т.е.
можно вычислить, взяв мгновенные
значения всех выборочных функций
ансамбля в момент времени
,
сложив эти значения и разделив на число
слагаемых, т.е.
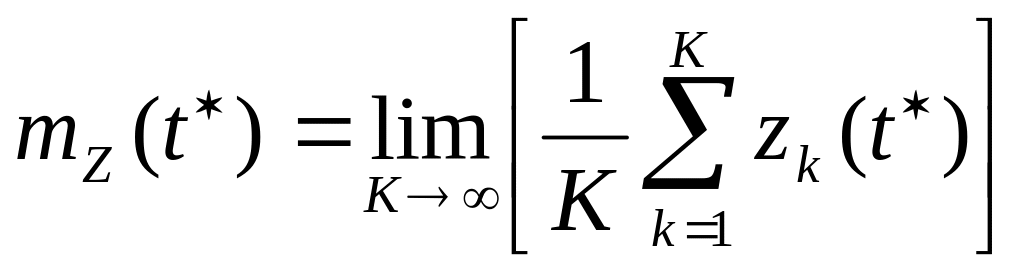 . (3)
. (3)
Аналогичным образом
ковариация
значений случайного процесса в два
различных момента времени
и
![]() вычисляется путем усреднения по ансамблю
произведений центрированных мгновенных
значений, взятых в эти моменты времени:
вычисляется путем усреднения по ансамблю
произведений центрированных мгновенных
значений, взятых в эти моменты времени:
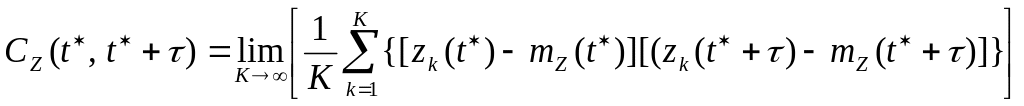 . (4)
. (4)
В формулах (3) и (4)
суммирование производится в предположении
равновероятности всех выборочных
функций. Расстояние
![]() между моментами времени в формуле (4)
называется сдвигом
или задержкой.
Заметим, что величина
между моментами времени в формуле (4)
называется сдвигом
или задержкой.
Заметим, что величина
![]() для нулевого сдвига (для
=0)
представляет собой дисперсию процесса
в момент времени
,
т.е.
для нулевого сдвига (для
=0)
представляет собой дисперсию процесса
в момент времени
,
т.е.
![]() .
.
В общем случае,
когда величины
![]() и
,
определенные уравнениями (3) и (4), зависят
от момента времени
,
случайный процесс
называется нестационарным.
В том частном случае, когда
и
,
не зависят от момента времени
,
случайный процесс называется слабо
стационарным
или стационарным
в широком
смысле.
Среднее значение слабо стационарного
процесса постоянно, а ковариационная
функция зависит только от сдвига времени
,
т.е.
и
,
определенные уравнениями (3) и (4), зависят
от момента времени
,
случайный процесс
называется нестационарным.
В том частном случае, когда
и
,
не зависят от момента времени
,
случайный процесс называется слабо
стационарным
или стационарным
в широком
смысле.
Среднее значение слабо стационарного
процесса постоянно, а ковариационная
функция зависит только от сдвига времени
,
т.е.
![]() , (5 а)
, (5 а)
![]() ,
(5 б)
,
(5 б)
![]() .
.
15. Процесс стационарный в узком смысле
Математическое ожидание и ковариацию называют соответственно моментом первого порядка и смешанным моментом. Для полного определения структуры случайного процесса нужно вычислить бесконечное число моментов и смешанных моментов высших порядков. В том случае, когда все моменты и смешанные моменты инвариантны во времени, случайный процесс называется строго стационарным или стационарным в узком смысле. Во многих приложениях проверка слабой стационарности позволяет обосновать строгую стационарность. Отметим, что для строго стационарного процесса функция и плотность распределения вероятностей в любом сечении одинаковы, т. е. они не зависят от времени:
![]() ,
(6 а)
,
(6 а)
![]() .
(6 б)
.
(6 б)
16. Случайные эргодические процессы, гауссов процесс
Формулы (3) и (4)
показывают, как можно определить
характеристики случайного процесса
путем усреднения по ансамблю в определенные
моменты времени. Однако в большинстве
случаев характеристики стационарного
случайного процесса можно вычислить,
усредняя по времени в пределах отдельной
выборочной функции, входящей в ансамбль.
Возьмем, например, k-ую
выборочную функцию
![]() ансамбля
Среднее значение
ансамбля
Среднее значение
![]() и ковариационная функция
и ковариационная функция
![]() ,
вычисленные по k-ой
реализации равны
,
вычисленные по k-ой
реализации равны
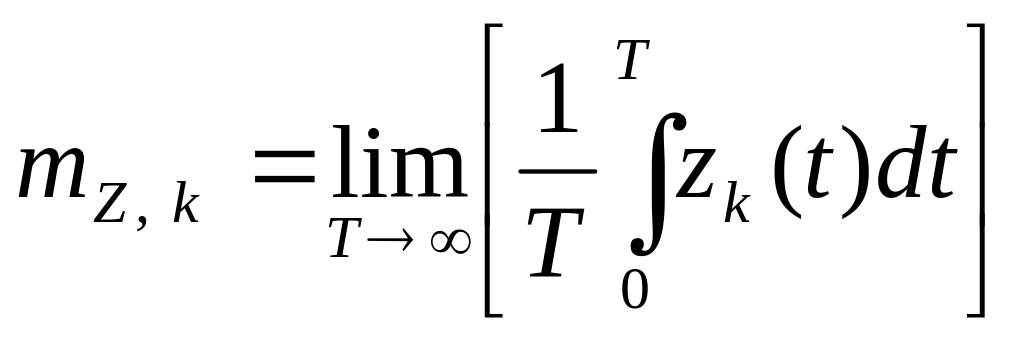 , (7
а)
, (7
а)
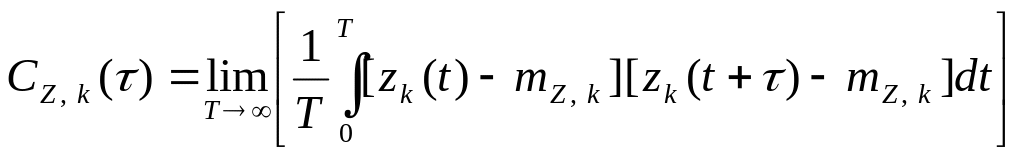 . (7
б)
. (7
б)
Если случайный
процесс
стационарен, а
и
,
вычисленные по различным реализациям
согласно формулам (7), совпадают, то
случайный процесс называется эргодическим.
Для эргодических процессов средние
значения и ковариационные функции,
полученные усреднением
по времени
(как и другие характеристики, вычисленные
усреднением по времени), равны аналогичным
характеристикам, найденным усреднением
по ансамблю,
т. е.
![]() и
и
![]() .
.
Эргодические случайные процессы образуют очень важный класс случайных процессов, поскольку все свойства эргодических процессов можно определить по единственной выборочной функции. На практике стационарные случайные процессы обычно оказываются эргодическими. По этой причине свойства стационарных случайных явлений можно определить по одной наблюдаемой реализации.
Особую практическую
значимость имеют стационарные процессы,
называемые гауссовыми
или нормальными
процессами.
Гауссов
случайный
процесс
характеризуется тем, что совместная
плотность распределения величин
,
определенных для всевозможных временных
сечений t,
является многомерной нормальной
(гауссовой) плотностью. Случайная выборка
![]() гауссова процесса, определенная для
сечений
гауссова процесса, определенная для
сечений
![]() ,
описывается N-мерным
совместным гауссовым распределением
компонент.
,
описывается N-мерным
совместным гауссовым распределением
компонент.
