9. Отображение цифрового сигнала в виде аналоговой функции времени

10. Сигнал как реализация процесса. Классификация процессов

В системах DCS передаваемые сигналы называется дискретными или цифровыми. Однако символы передаваемого сообщения, берущиеся из дискретного и конечного алфавита, преобразуются в сигналы, которые являются аналоговыми. Например, полосовой сигнал

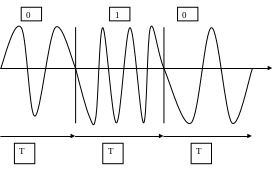
В этом примере для передачи разных символов из бинарного алфавита используется гармонический аналоговый сигнал. Причем в этом сигнале каждому символу соответствует своя частота на интервале передачи бита. Несмотря на то, что для передачи используется аналоговая функция времени, сигнал все же называется цифровым. Будем обозначать некоторый сигнал, как z(t). В теории математическая модель, с помощью которой описывается механизм получения сигнала z(t), называется процессом. Различают детерминированные и случайные процессы. Детерминированные процессы описываются явными математическими формулами. Это позволяет получать точные значения функции z(t) для любого момента времени t.

Случайные процессы нельзя описать во всех деталях. В любой момент времени t значение такого процесса z(t) не может быть вычислено точно, так как эта величина является случайной.

Детерминированные процессы подразделяются на периодические и непериодические.

Случайные процессы делятся на две группы: стационарные и нестационарные.

11. Гармонические и переходные непериодические процессы Гармонический процесс - это периодический процесс, поведение которого во времени математически выражается формулой , где А_о - амплитуда, f_g - циклическая частота в герцах, если t измеря­ется в секундах, Q - начальный фазовый угол в радианах, z(t) -мгновенное значение в момент t.

При практическом анализе гармонических процессов фазовый угол Q часто игнорируется. В этом случае .

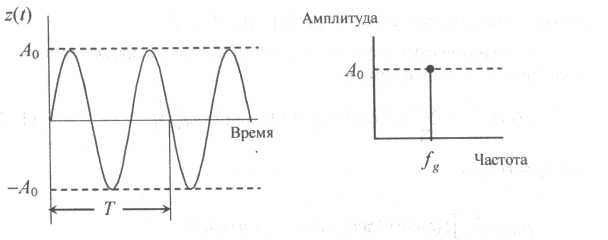
Уравнение графически можно изобразить либо в виде зависимо­сти мгновенного значения oт времени, либо в виде зависимости ам­плитуды от частоты (частотного спектра); оба способа показаны на рисунке

Интервал времени, на котором происходит одно полное колеба­ние или цикл гармонического процесса, называется периодом T_g. Чис­ло циклов в единицу времени называется частотой f_g . Частота и пе­риод связаны соотношением

Спектры, задающие непрерывную за­висимость амплитуды от частоты, называются дис­кретными или линейчатыми.

Переходные процессы - это все непериодиче­ские процессы, за исключением почти периодических процессов. Дру­гими словами, к переходным относятся все процессы, которые можно задать какой-либо функцией времени, за исключением процессов, рас­смотренных выше.

К переходным процессам приводят многочисленные и самые разнообразные явления.

Важная особенность переходных процессов, отличающая их от периодических и почти периодических процессов, состоит в том, что их нельзя охарактеризовать дискретным спектром. В большинстве случаев для переходных процессов можно получить непрерывное спектральное представление, используя преобразование Фурье вида

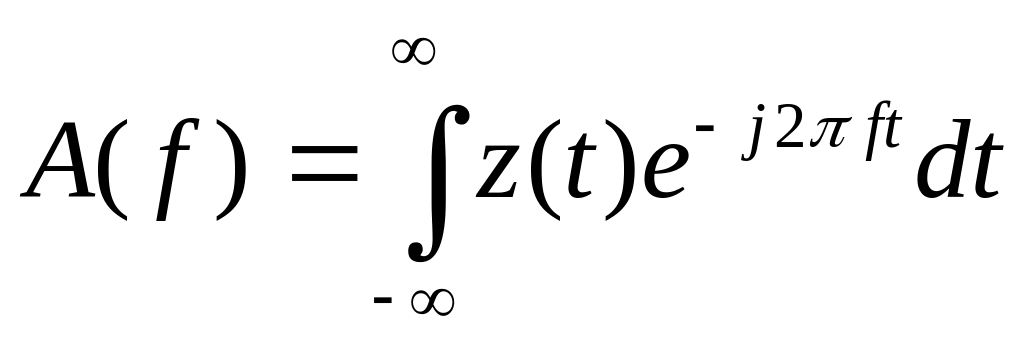
где j - мнимая единица. Вообще говоря, преобразование Фурье A(f) является комплексной (комплекснозначной) величиной.