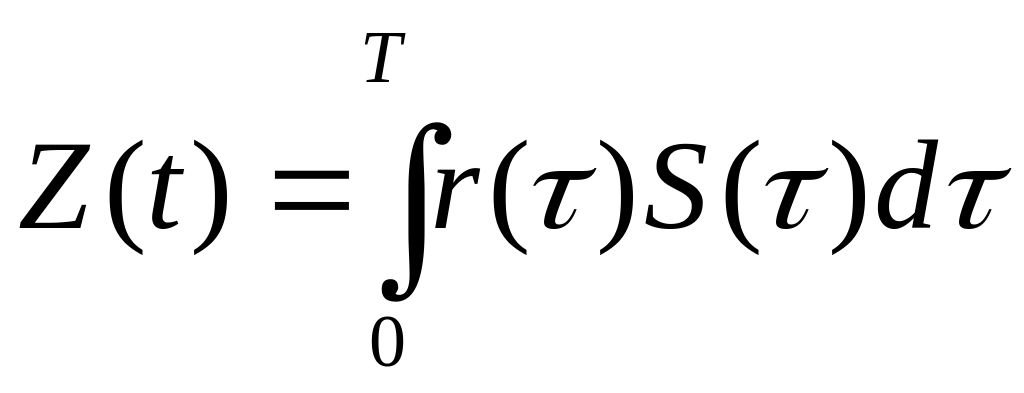- •1. Основные определения: информация, сообщение, система связи, сигнал, алфавит.
- •2. Функциональная система цифровой системы связи.
- •3. Преимущества и недостатки цифровой связи
- •4.Четырехуровневая коммуникационная система
- •5. Эталонная модель (osi): стек протоколов
- •6. Уровни модели взаимодействия открытых систем osi
- •Блочная диаграмма типичной системы цифровой связи от источника к передатчику
- •Блочная диаграмма типичной системы цифровой связи от приемника к потребителю информации
- •9. Отображение цифрового сигнала в виде аналоговой функции времени
- •10. Сигнал как реализация процесса. Классификация процессов
- •12. Полигармонические и почти периодические процессы
- •13. Определение случайного процесса
- •14. Процесс стационарный в широком смысле
- •15. Процесс стационарный в узком смысле
- •16. Случайные эргодические процессы, гауссов процесс
- •17. Процессы авторегрессии
- •18. Ковариационная и корреляционная матрицы случайного процесса, автоковариационная и автокорреляционная функции
- •19. Оценивание ковариационной и корреляционной матриц случайного процесса и автоковариационной и автокорреляционной функций
- •20. Случайные нестационарные процессы, характеристики случайных процессов
- •21. Классификация шумов в системах связи.
- •22. Определение спектральной плотности мощности. Теорема Винера-Хинчина.
- •23. Непрерывное преобразования Фурье
- •24. Финитное преобразование Фурье
- •25. Дискретное преобразование Фурье (дпф).
- •26. Свойства дпф.
- •27. Оценивание спектральной плотности с помощью дпф
- •28. Модель белого шума.
- •29. Линейные системы с постоянными параметрами.
- •Характеристики линейных систем с постоянными параметрами.
- •31. Последовательное включение систем с постоянными параметрами.
- •32. Связь спектральных плотностей входного и выходного процессов линейной системы с постоянными параметрами.
- •3 5. Узкополосные и широкополосные сигналы.
- •36. Критерии определения ширины полосы.
- •Форматирование текстовой информации в системах dcs.
- •38. Теорема о дискретном представлении. Критерий Найквиста. Инженерный критерий Найквиста.
- •Дискретизация с помощью идеальных единичных импульсов (идеальная дискретизация).
- •Естественная дискретизация.
- •41.Дискретизация по методу «выборка-хранение».
- •42.Квантование амплитуды и характеристики.
- •45.Шум квантования.
- •46.Импульсно кодовая модуляция квантованных выборок аналогового сигнала.
- •47.Кодирование источников определения.
- •48.Дискретные источники и их характеристики.
- •49.Типы дискретных источников.
- •50.Свойства кодов.
- •51. Показатели кодирования
- •52. Кодирование источников без памяти: код шеннона-фано
- •54. Кодирование источников с памятью: методы подавления нулей и групповое кодирование
- •55. Кодирование источников с памятью: методы подстановки образцов и дифференциальное сжатие
- •56. Униполярные и биполярные сигналы pcm
- •57. Сигналы рсм в кодировке nrz (nrz-l, nrz-m, nrz-s)
- •58. Кодировки nrz-ami и rz-ami
- •59. Фазовое кодирование
- •60. Кодирование модуляцией задержки
- •61. Многоуровневое кодирование рсм. Достоинства и недостатки
- •62. Искажение сигналов шумом awgn
- •63. Межсимвольная интерференция
- •64. Обобщенная схема передачи узкополосного сигнала
- •65. Основные этапы демодуляции/обнаружения
- •68. Униполярная передача двоичных сигналов
- •69. Биполярная передача двоичных сигналов
- •70. Эквивалентная модель системы dcs
- •71. Импульсы Найквиста
- •72. Компенсация искажений с помощью выравнивания
- •73. Виды выравнивания и типы эквалайзеров.
- •74. Дискретный канал без памяти
- •75. Теорема кодирования канала
- •76. Теорема о пропускной способности канала
- •Зачем нужна широкополосная модуляция?
- •78, 79. Амплитудная и частотная модуляция (ask и fsk)
- •80. Частотная манипуляция и бинарная частотная манипуляция
- •81. Бинарная фазовая манипуляция, квадратурная фазовая манипуляция
- •82. Амплитудно-фазовая манипуляция (арк)
- •83. Определение полосовой демодуляции и ее виды
- •84. Ресурс связи и способы его распределения
- •85. Сигналы, ортогональные во времени и по частоте
- •86. Уплотнение/множественный доступ с частотным разделением
- •87. Множественный доступ с временным разделением
65. Основные этапы демодуляции/обнаружения
Демодуляцией называется процесс восстановление переданного сигнала по его принятой искаженной версии. Обнаружением называется принятие решения относительно цифрового значения восстановления сигнала. Обычно эти оба процесса объединяют под термином демодуляции:
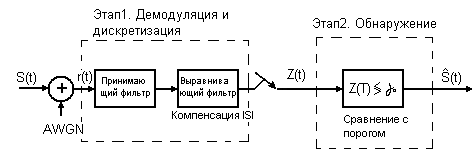
В начале искаженная
версия
сигнала
![]() поступает на принимающий фильтр. Этот
фильтр выполняет задачу восстановления
переданного импульса с максимальным
отношением «сигнал \ шум» (SNR).
Фильтр, выполняющий эту задачу, называется
согласованным фильтром или коррелятором.
За принимающим фильтром может находиться
схема выравнивания, которая необходима
для систем, в которых заметна межсимвольная
интерференция. Рассмотрим процесс
обработки на одном ИПБ [0, Т].
поступает на принимающий фильтр. Этот
фильтр выполняет задачу восстановления
переданного импульса с максимальным
отношением «сигнал \ шум» (SNR).
Фильтр, выполняющий эту задачу, называется
согласованным фильтром или коррелятором.
За принимающим фильтром может находиться
схема выравнивания, которая необходима
для систем, в которых заметна межсимвольная
интерференция. Рассмотрим процесс
обработки на одном ИПБ [0, Т].
На схему дискретизации в момент времени Т поступает некоторое мгновенное значение Z(T), которое называется тестовой статистикой. Значение Z(T) прямо пропорционально энергии сигнала и обратно – шуму. Выход устройства дискретизации называется додетекторной точкой.
Z(T)
можно представить в виде
![]() , где
, где
![]() - ожидаемый компонент статистики Z(T)
(её среднее),
- ожидаемый компонент статистики Z(T)
(её среднее),
![]() - компонент шума с нулевым средним и
дисперсией
- компонент шума с нулевым средним и
дисперсией
![]() .
.
Т.о. Z(T)
– случайная величина со средним равным
![]() или
или
![]() в зависимости от того, передан на интервал
[0, T]
0 или 1.
в зависимости от того, передан на интервал
[0, T]
0 или 1.
После того, как принятый сигнал преобразован в величину Z(T) реальная форма сигнала значения не имеет. Любые сигналы, отображаемые устройством дискретизации в одно и то же значение Z(T) для схемы обнаружения являются идентичными. Величина Z(T) зависит от энергии принятого сигнала.
На этапе 2 проверка
цифровых значений (0, 1) выполняется как
проверка статистической гипотезы.
Гипотеза
![]() утверждает, что передан 0, а гипотеза
утверждает, что передан 0, а гипотеза
![]() - 1. Проверка выполняется сравнением
тестовой статистики с пороговым значением
- 1. Проверка выполняется сравнением
тестовой статистики с пороговым значением
![]() .
.
Если Z(T)>
,
то принимается решение о том, что передана
1. Подтверждение гипотезы
происходит тогда, когда Z(T)<
.
При Z(T)=
решение может быть любым. Согласно
принципу максимального правдоподобия
порог
задается в т. пересечения 2-х условных
плотностей
![]() и
и
![]() .
Т.к. обе плотности симметричны относительно
т.
.
Т.к. обе плотности симметричны относительно
т.
![]() и
и
![]() ,
порог максимального правдоподобия :
,
порог максимального правдоподобия :
![]() .
.
66-67. Согласованный фильтр и коррелятор
В аналоговой связи
для характеристики ее качества
используется показатель сигнал – шум
![]() ,
где S
– средняя мощность сигнала,
,
где S
– средняя мощность сигнала,
![]() - средняя мощность шума. В цифровой связи
используется нормированная версия
этого показателя
- средняя мощность шума. В цифровой связи
используется нормированная версия
этого показателя
![]() ,
где
,
где
![]() - энергия бита на [0, Т], умноженная на
длину этого интервала (
- энергия бита на [0, Т], умноженная на
длину этого интервала (![]() ),
),
![]() - мощность шума деленная на ширину
полосы
- мощность шума деленная на ширину
полосы
![]() .
.
Т.о. величина
 - скорость передачи бит/сек.
- скорость передачи бит/сек.
Чем больше соотношение , тем больше вероятность правильного обнаружения сигнала.
Оптимальный
согласованный принимающий фильтр –
это линейный фильтр, который обеспечивает
для заданного сигнала S(t)
максимальное отношение “ сигнал/шум
”. Предположим, что на схеме обработки
отсутствует необязательный выравнивающий
фильтр, а искажение определяется только
шумом AWGN.
Оптимальный фильтр обеспечивает
максимальное соотношение «сигнал/шум»
в момент времени t=T:
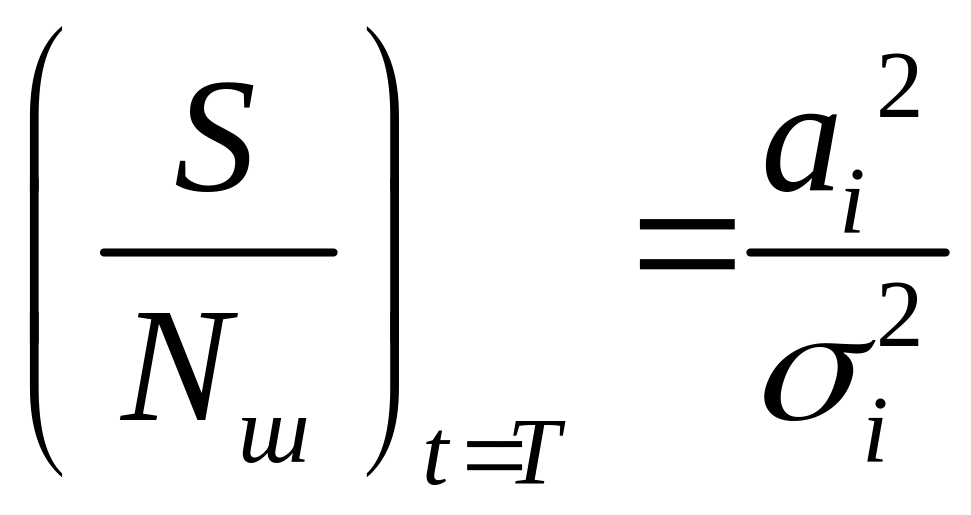 .
Это отношение обеспечивается тестовой
статистикой
.
Это отношение обеспечивается тестовой
статистикой
![]() .
Max
SNT
для заданного сигнала S(t)
будет обеспечена тогда, когда этот
сигнал пропускается через фильтр с
частотной характеристикой
.
Max
SNT
для заданного сигнала S(t)
будет обеспечена тогда, когда этот
сигнал пропускается через фильтр с
частотной характеристикой
![]() ,
где k
– константа,
,
где k
– константа,
![]() - комплексно – сопряженное преобразование
Фурье сигнала S(t).Импульсная
характеристика оптимального согласованного
фильтра получается применением
преобразования Фурье к
- комплексно – сопряженное преобразование
Фурье сигнала S(t).Импульсная
характеристика оптимального согласованного
фильтра получается применением
преобразования Фурье к
![]() (*)
(*)
Т.о. импульсная характеристика оптимально согласованного с сигналом фильтра должна быть зеркальным отображением сигнала S(t), сдвинутым на интервал длиной Т. Выход согласованного фильтра представляет собой свертку сигнала S(t) с его импульсной характеристикой.
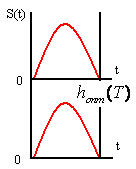
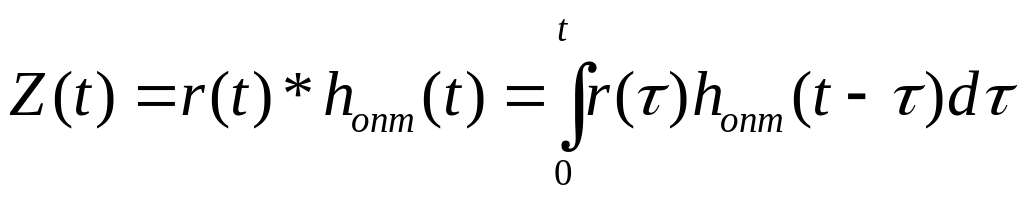 .
Подставим
вместо t
T
получим:
.
Подставим
вместо t
T
получим:
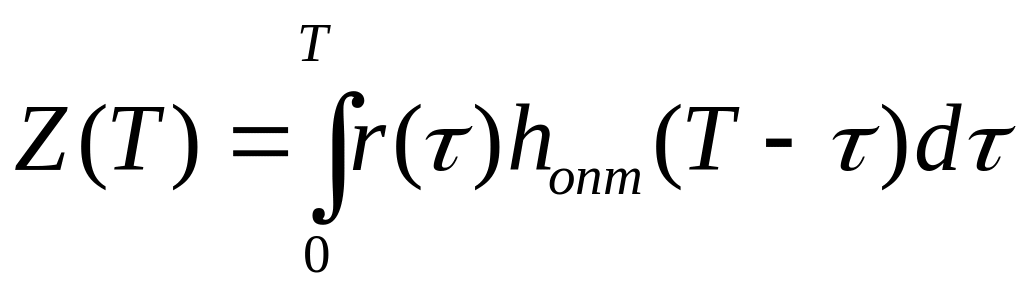 .
Подставим соотношение (*):
.
Подставим соотношение (*):