37. Форматирование текстовой информации в системах dcs.

Буквенно-цифровой текст должен быть преобразован в поток битов. Для такого преобразования используется один или несколько стандартных форматов, которые называются методами знакового кодирования: ASCII, EBCDIC, код Бодо. Следует отличать алфавит источника и алфавит символов, используемый для передачи. Составляющие алфавита источника, называемые знаками алфавита, используемые для передачи, содержит символы. Поток битов разделяется на последовательные группы по к битов. Значит каждая группа может содержать символ, взятый из алфавита .

Система, в которой алфавит передаваемых символов равен М, называется М-арной. При к=1 речь идет о бинарной системе. Модулятор может генерировать в этом случае сигнал , передающий на интервале [0,T] бинарный нуль, для бинарной единицы. Для к=2 (М=4) передача называется четверичной (4-хуровненой). В этом случае для передачи используются 00 – S0, 11-S3 и т. д. При М-арной передаче количество сигналов, которые должен генерировать модулятор, изменяются от 0 до М-1. Границы кодов знаков и границы передаваемых символов могут не совпадать. При приеме конечный получатель присваивает полученной последовательности сигналов конкретное текстовое значение. (для примера 2,8,4,10,1.12)

38. Теорема о дискретном представлении. Критерий Найквиста. Инженерный критерий Найквиста.

Д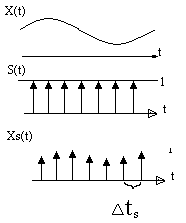 искретизация может быть реализована по-разному, но основное ее назначение получение электрических импульсов, амплитуда которых определяется соответственными значениями аналогового сигнала, выбранными в дискретные моменты времени. Исходный аналоговый сигнал можно восстанавливать (низкочастотная фильтрация). Последовательность импульсов после дискретизации аналогового сигнала называют сигналом в Амплитудно-Импульсной Модуляции (PUM). Чтоб иметь возможность восстановить исходный аналоговый сигнал у его дискретной версии необходимо выполнить условие: Аналоговый сигнал с ограниченной полосой, не имеющей спектральных компонентов с частотами, превышающими частоту , однозначно определяется дискретизированной версией, если интервал дискретизации - это и есть теорема о равномерном представлении. Если , то (это критерий Найквеста, если знак равно, то это частота Найквеста, инженерный критерий Найквеста - ), то есть для полного восстановления дискретного аналогового сигнала нужно, чтоб частота дискретизации была не меньше, чем 2 максимальных частоты спектра.

39. Дискретизация с помощью идеальных единичных импульсов (идеальная дискретизация).

П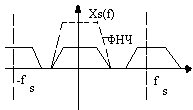 усть X(t) аналоговый сигнал, амплитудный спектр которого есть х(t). Этот спектр ограничивает полосу: . Идеальную дискретизацию можно получить с помощью умножения x(t) на серию единичных импульсов Дирака . Дискретный сигнал обозначим , где . Преобразование Фурье для произведения эквивалентно свертке преобразований Фурье этих функций. Спектр дискретной версии .

Эта формула показывает: что если не учитывать , то спектр содержит копию исходного аналогового спектра, повторяющегося по частоте с интервалом . На рисунке изображен случай спектра с частотой дискретизации большей . Спектральные копии не накладываются друг на друга (имеет место разделение). Применив ФНЧ к серии импульсов можно вырезать в спектре копию соответствующую спектру аналогового сигнала.

Таким образом выполняется процесс восстановления аналогового сигнала из его дискретизированной версии. Если частота дискретизации недостоточна и критерий Найквеста не выполняется, то спектральные копии накладываются друг на друга. Поскольку по эти формулы суммируются, то результирующий спектр будет иметь жирный вид – никакими методами обработки восстановить сигнал нельзя. Явление, обусловленной недостаточной частотой дискретизации, называется наложением ( aliasing) частот.