29. Линейные системы с постоянными параметрами.
Линейной системой называется передающая система с 2 четко определенными характеристиками:
- входная характеристика (входное воздействие)
- выходная характеристика.
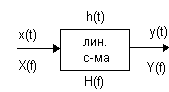
Входное воздействие представляется обычно сигналом x(t), а отклик – y(t), причем зависимость между выходом и входом линейная. Входные и выходные сигналы могут задаваться с помощью преобраз. Фурье X(f) и Y(f).
Система называется системой с постоянными параметрами, если ее свойства не изменяются во времени. Другое название: система, инвариантная относительно времени.
Неизменяемость свойств не означает, что сигналы x(t) и y(t) не изменяются во времени.
Определение
линейная означает следующее: пусть x
отображается в y
с помощью функции
.
Система линейна, если она аддитивна и
однородна.
Свойство аддитивности:
Т.е. отклик системы
на воздействие суммы 2 сигналов
равен сумме откликов на каждый сигнал
в отдельности.
Свойство однородности:
Т.е. отклик системы на сигнал x, умноженный на константу c, равен произведению этой же константы на отклик, вызываемый входным сигналом x.
Характеристики линейных систем с постоянными параметрами.
Динамика систем,
инвариантных относительно времени,
описывается во временной области
функцией, называемой импульсной
характеристикой: обозначается h(t),
а ее преобразование Фурье H(f).
h(t)
определяется как реакция системы на
входной сигнал, представляющий собой
единичный импульс Дирака. Тогда отклик
y(t)
на любой входной сигнал x(t)
описывается интегралом свертки:
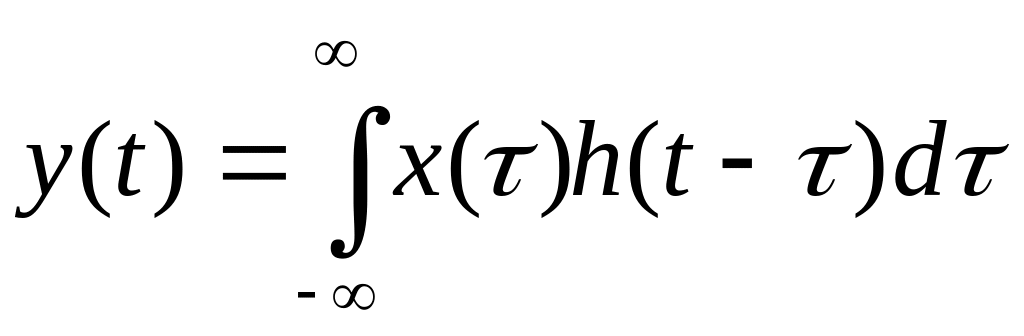(1)
Для того, чтобы
система была физически реализуемой,
необходимо чтобы сигнал на выходе мог
появиться только после того, как появится
сигнал на входе. Если момент появления
сигнала на входе обозначить через 0, то
интеграл свертки:
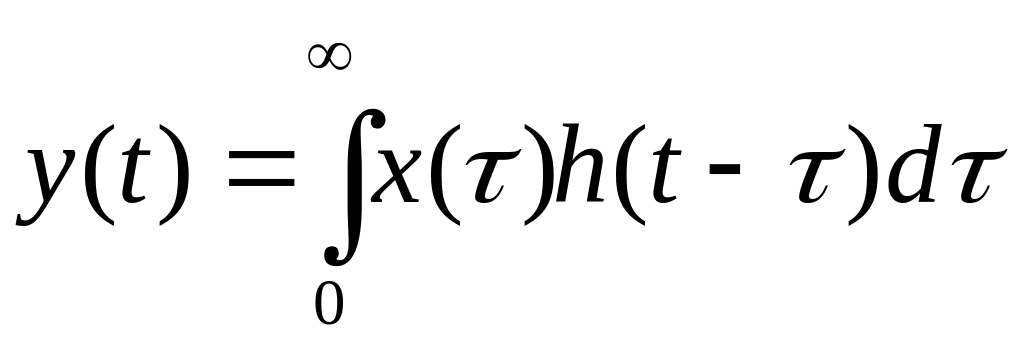(2)
или
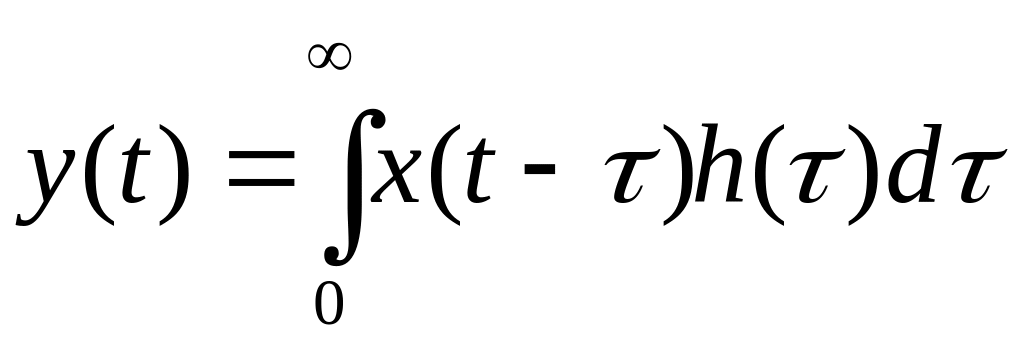(3)
Интегралы из формул
2 и 3 записываются короче:
y(t)=x(t)*h(t)=h(t)*(x(t))
(4) где * -обозначение свертки. Свертка
во временной области эквивалентна
произведению в частотной области. Т.о.,
применим преобразование Фурье к левой
и правой частям уравнения 2 или 3, что
приводит к следующему соотношению:
Y(f)=X(f)H(f)=H(f)X(f).
(5) Функция H(f)-преобразование
Фурье импульсной характеристики h(t):
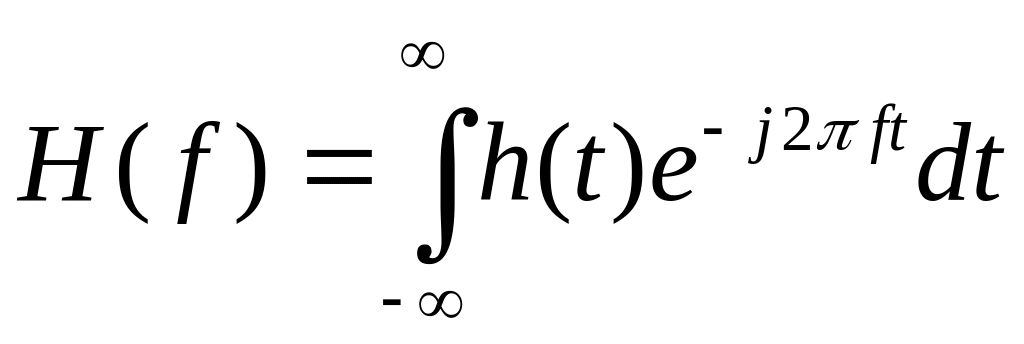(6)
Эта функция
комплексная. Обычно ее представляют в
полярной форме:
,
(7) где
-модуль,
-аргумент.
Сама функция H(f)
называется частотной характеристикой
системы. Функция
-амплитудная
характеристика или амплитудно-частотная
характеристика (АЧХ);
-фазочастотная
характеристика (ФЧХ).
Т.о., соотношение (5) интерпретируется: если входной сигнал x(t) является «чистой» гармоникой с частотой f, то на выходе - гармоника с частотой f и амплитудой, умноженной на , и сдвигом по фазе . Частотная характеристика обладает следующими свойствами симметрии:
H(f)=H*(-f); 2)
;
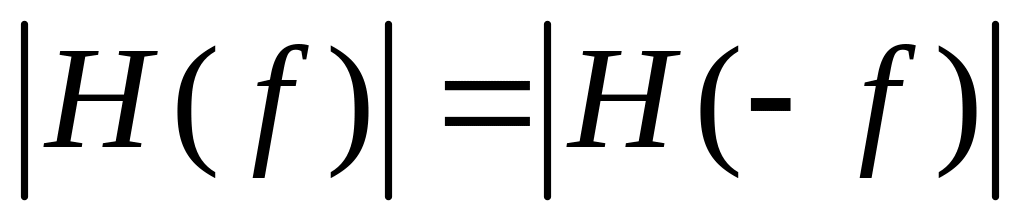3)
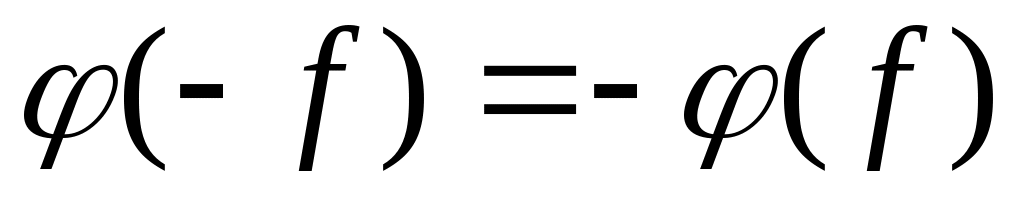
Пусть линейная
система образована последовательными
включениями 2-х линейных систем с
и
,
и между этими системами нет обратных
связей.
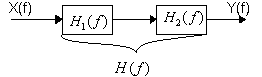
Тогда частотная характеристика общей системы имеет следующие свойства:
