22. Определение спектральной плотности мощности. Теорема Винера-Хинчина.
Частотный анализ случайных шумов выполняют на основе функций S(f), где f- частота. Функция S(f)- спектральная плотность мощности шума. Для стационарного случайного процесса спектральная плотность определяется так:
- пусть задана
,
интеграл от которой ограничен
:
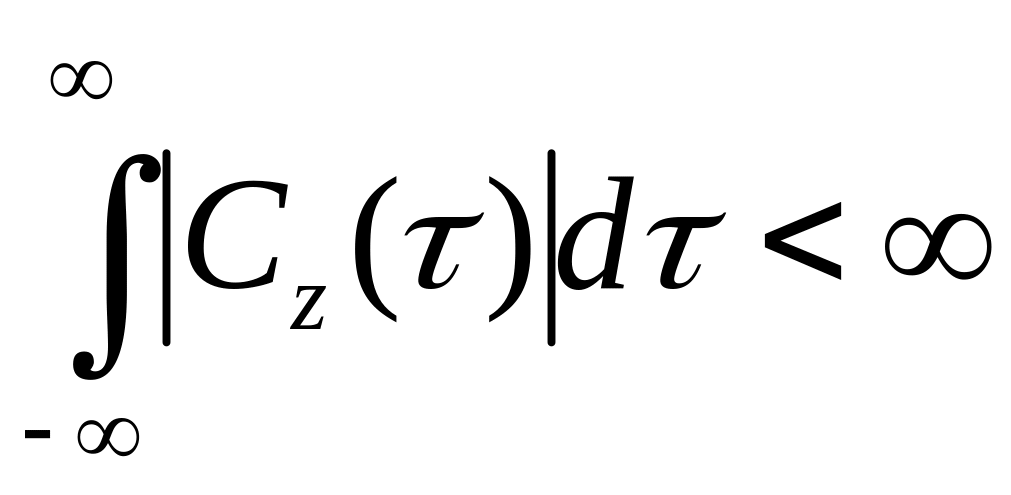
Тогда плотность - преобразование Фурье от функции :
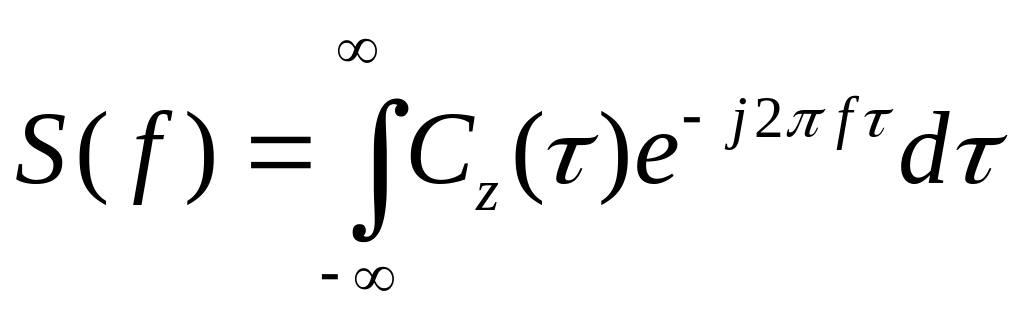(1)
С другой стороны,
из функции S(f)
можно получить корреляционную функцию:
(2)
Т.к. для случайного процесса автоковариационная функция и спектральная плотность являются взаимными трансформантами Фурье. Соотношения, описываемые формулами 1 и 2, называются уравнениями Винера-Хинчина.
Поскольку ковариационная функция стационарного процесса является четной, то и спектр является четной функцией частоты S(f)= S(-f). Теоретически спектр определен для отрицательных частот, поэтому он называется двухсторонней спектральной плотностью. И поэтому на практике часто используют односторонние плотности:
и существуют только
для положительных частот.
Важным свойством
теплового шума, описываемого моделью
случайного процесса, является тот факт,
что его спектральная плотность постоянна
для всех частот:
Делитель 2 применяется
для того, чтобы показать, что это
двухсторонняя плотность.
-
односторонняя плотность.
К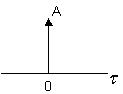
овариационная
функция такого шума задается выражением:
,
где
-импульсная
функция Дирака, нереальный сигнал.
Считается, что
имеет
бесконечную амплитуду, нулевую ширину
и единичную площадь. Любая величина А*
изображается как импульс высотой А в
т.
и равный 0 при др.
.
Таким образом,
ковариация шума - это мгновенный импульс
в т.
(рис1),
а спектральная плотность шума имеет
следующий вид (рис 2)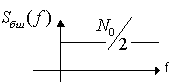
Случайный процесс с постоянной спектральной плотностью для всех частот называется белым шумом.
Рис1 Рис 2
23. Непрерывное преобразования Фурье
Преобразование
Фурье,
или спектр,
произвольной непрерывной функции
,
определяется следующим образом:
,
(5.1) где
оператор, преобразующий функцию
в другую функцию
.
Как
,
так и
могут быть комплексными функциями
действительного аргумента. Нетрудно
показать, что для действительных функций
преобразование Фурье имеет
комплексно-сопряженную симметрию:
,
(5.2) где звездочка в обозначении
означает, что
и
сопряженные комплексные числа.
Основным свойством
преобразования Фурье является его
способность различать колебания
различных частот в аддитивных комбинациях.
Иначе говоря, если функция
есть сумма конечного числа гармонических
функций вида
,
т. е.
, (5.3)
то спектр имеет вид
. (5.4)
В формуле (5.4)
фигурирует единичная импульсная функция
,
называемая дельта-функцией;
она определяется выражением
Таким образом, сумма гармонических колебаний, перекрывающихся во времени (накладывающихся друг на друга), преобразуется в сумму импульсов (по частоте), которые, по определению, не перекрываются. В терминах, применяемых при анализе сигналов, преобразование Фурье вводится для того, чтобы представить процесс в частотной области, а независимая переменная f аргумент преобразования Фурье понимается как частота, и, если время измеряется в секундах, то частота – в герцах (Гц). Очевидно, анализ структуры такой функции, как функция (4.3), гораздо удобнее проводить в частотной области, нежели во временной.
Преобразование
Фурье обладает свойством линейности,
которое описывается соотношением
. (5.5)
Существует обратное преобразование Фурье, задаваемое выражением
. (5.6)