
- •Раздел II
- •Основы промышленной эдектроники
- •Тема № 4 электронные приборы
- •Лекция 12. Полупроводниковые приборы
- •1.Классификация полупроводниковых электронных приборов
- •2. Типы проводимости полупроводниковых материалов. Электронно-дырочный переход. Основные параметры полупроводниковых диодов.
- •3. Биполярные транзисторы.
- •4. Полевые транзисторы
- •5. Тиристоры
- •Тема 5. Электронные устройства Лекция 13. Преобразователи напряжения
- •Выпрямители
- •Сглаживающие фильтры
- •3.Стабилизаторы напряжения
- •Лекция 14 резистивные усилители низкой частоты
- •1.Принцип работы каскада по схеме с общим эмиттером
- •2.Дифференциальный усилитель
- •Усилитель по схеме с общим коллектором
- •4.Операционный усилитель
- •Тема 6. Импульсные устройства Лекция 15. Элементы импульсных устройств
- •1.Общие сведения об импульсных сигналах
- •Электронные ключи
- •Компараторы
- •Лекция 16. Генераторы импульсных сигналов
- •1. Формирующие цепи
- •2. Мультивибраторы
- •Период повторения
- •Скважность
- •3. Генераторы линейно изменяющегося напряжения.
- •Если напряжение на входе оу постоянное, то получаем
- •Напряжением открывается диод d1. На интеграторе начинается формирование линейно падающего напряжения. Напряжение uoc также линейно убывает и в момент t3 принимает значение
- •Далее значение uглин периодически изменяется от –0,79 в до 3,2 в, а uос от –2,32 в до 4,31 в.
- •Тема 7. Цифровые устройства Лекция 17. Введение в цифровую электронику
- •Общие сведения о цифровых сигналах.
- •Основные операции и элементы алгебры логики.
- •О сновные теоремы алгебры логики.
- •Булевы функции (функции логики).
- •Для элемента "или-не"
- •Для элемента "и-не"
- •Минимизация булевых функций
- •Комбинационные устройства
Для элемента "или-не"
операция "НЕ"
|
операция "ИЛИ"
|
операция "И"
|

Для элемента "и-не"
операция "НЕ"
|
операция "ИЛИ"
|
операция "И"
|
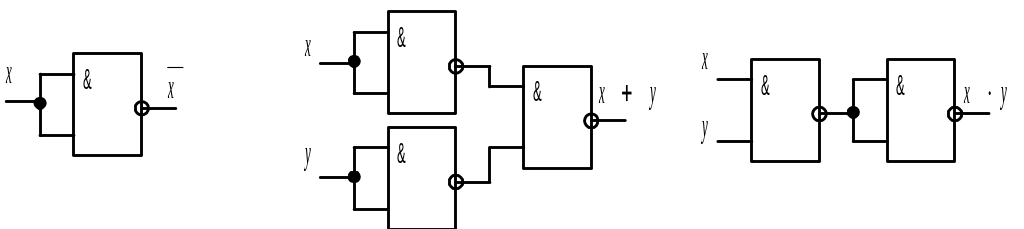
В микросхемном исполнении элементы "ИЛИ-НЕ" обозначаются индексами ЛЕ, элементы "И-НЕ" – индексами ЛА. Например, микросхема К555 ЛЕ1 имеет в своем составе четыре элемента "ИЛИ-НЕ" на два входа каждый.
Минимизация булевых функций
Булевы функции в СДНФ и в СКНФ обычно избыточны. Поэтому этапу построения схемы должно предшествовать упрощение формул или минимизация. Цель минимизации – получить минимально необходимое количество логических элементов в схеме. В основу минимизации положены правила и законы булевой алгебры. Чаще других применяется теорема склеивания:
![]()
Для
применения этой теоремы в функции,
представленной в СДНФ отыскиваются
слагаемые, отличающиеся только одним
аргументом, и склеиваются. Когда все
операции склеивания выполнены, можно
проверить возможность применения
закона поглощения. Для примера проведем
минимизацию функции (17.4). Добавим в
выражение (17.4) еще два слагаемых
![]() .
От этого значение функции не изменится
(правило 3).
.
От этого значение функции не изменится
(правило 3).
![]()
Проведем группирование и возможные склеивания:
![]() (17.6)
(17.6)
Вместо четырех слагаемых третьего ранга (17.4) получили три слагаемых второго ранга. Схема, соответствующая (17.6) приведена на рис. 17.6.
В
инженерной практике для минимизации
логических функций, как правило,
применяют карты (матрицы) Карно. Карта
Карно представляет прямоугольник,
разбитый на квадраты. Число квадратов
равно числу возможных комбинаций, т.
е.
![]() .
Каждый квадрат соответствует определенной
комбинации аргументов (см. рис. 17.7а).
Комбинации соседних квадратов должны
отличаться не более чем одним аргументом.
Для примера на рис.17.7а все возможные
комбинации функции
.
Каждый квадрат соответствует определенной
комбинации аргументов (см. рис. 17.7а).
Комбинации соседних квадратов должны
отличаться не более чем одним аргументом.
Для примера на рис.17.7а все возможные
комбинации функции
![]() Внесены в квадраты карты Карно.
Внесены в квадраты карты Карно.
В целях минимизации карта Карно заполняется
"1" и "0". Знак "1" записывается
в тот квадрат, комбинация которого
соответствует значению F
= 1. В остальные квадраты записываются
"0" (рис. 17.7б). После заполнения
целях минимизации карта Карно заполняется
"1" и "0". Знак "1" записывается
в тот квадрат, комбинация которого
соответствует значению F
= 1. В остальные квадраты записываются
"0" (рис. 17.7б). После заполнения
к вадраты
с "1" объединяют в контуры. Объединить
можно 2, 4, 8 квадратов и т. д. Это
равносильно объединению слагаемых
функции для склеивания. Каждый квадрат
может входить в несколько соседних
контуров. Возможно объединение крайних
квадратов на противоположных сторонах
карты.
вадраты
с "1" объединяют в контуры. Объединить
можно 2, 4, 8 квадратов и т. д. Это
равносильно объединению слагаемых
функции для склеивания. Каждый квадрат
может входить в несколько соседних
контуров. Возможно объединение крайних
квадратов на противоположных сторонах
карты.
Объединением двух квадратов исключается один аргумент, четырех квадратов – два аргумента и т. д. В минимизированном выражении функции остаются только те аргументы, значение которых одинаково во всех квадратах контура. Например, для рис. 17.7б результат минимизации будет иметь вид
![]()
и полностью совпадает с выражением (17.6).
Комбинационные устройства
Комбинационными называются логические устройства, выходные функции которых определяются входными логическими функциями в момент их воздействия. К комбинационным устройствам относятся шифраторы, дешифраторы, преобразователи кодов, мультиплексоры и демультиплексоры, сумматоры и компараторы.
Разрабатывать комбинационные устройства целесообразно в следующей последовательности:
составляется таблица истинности;
с помощью карты Карно находится минимизированное выражение логической функции;
составляется логическая схема.
Рассмотрим принцип построения некоторых комбинационных устройств.
Шифраторы предназначены для преобразования цифровой информации из десятичной системы счисления в двоичную. Для примера рассмотрим принцип построения схемы преобразования цифр от "0" до "9" в код 8-4-2-1. У такой схемы десять входов и четыре выхода. Наличие на одном из входов сигнала "1" приводит к появлению на выходах соответствующей кодовой комбинации.
Приведенному
словесному описанию соответствует
комбинированная таблица 17.2. Она
определяет все возможные состояния
входов и соответствующие им состояния
выходов. Символами
![]() обозначены
обозначены
Таблица 17.2
№ п/п |
Код 1 из10 |
Код 8-4-2-1 |
||||||||||||
x0 |
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
x7 |
x8 |
x9 |
Q4 |
Q3 |
Q2 |
Q1 |
|
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
2 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
3 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
4 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
5 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
6 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
7 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
8 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
9 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
сигналы
на входе шифратора (аргументы). Символами
![]() - выходы шифратора (функции). Из таблицы
видно, что функция
- выходы шифратора (функции). Из таблицы
видно, что функция
![]() (колонка под
)
равна 1 в тех случаях, когда на вход
поступает информация о цифрах 1; 3; 5; 7
или 9. Поэтому можно записать
(колонка под
)
равна 1 в тех случаях, когда на вход
поступает информация о цифрах 1; 3; 5; 7
или 9. Поэтому можно записать
![]() .
.
Теперь очевидно, что

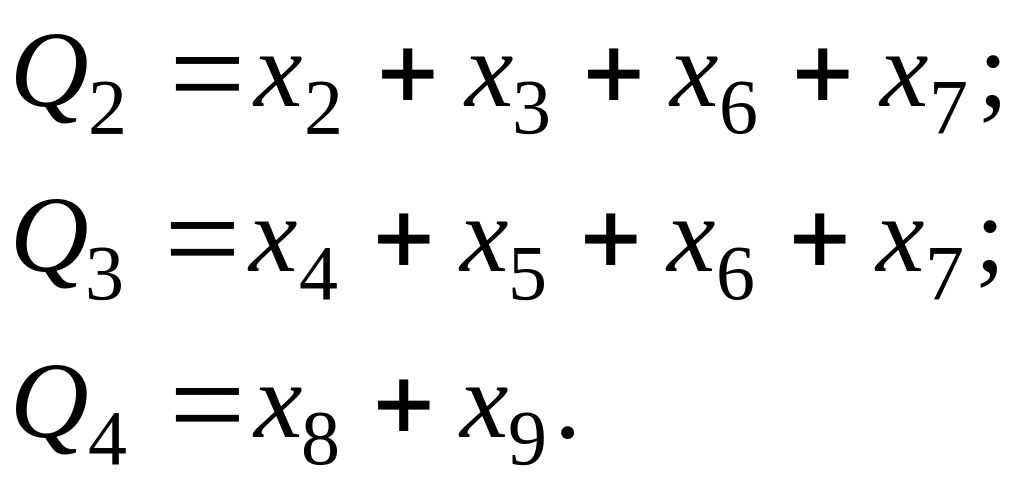
Этап минимизации в данном случае отпадает, т. к. все функции представляют собой элементарные логические суммы. Схема шифратора, выполненная на элементах "ИЛИ", приведена на рис. 17.7а. Выходным кодом шифратора может быть любой другой код. Принцип построения остается прежним. Управляющим сигналом может быть "0". Тогда схема может быть построена на элементах "И".
Шифраторы
выпускаются в микросхемном исполнении,
например КМ555 ИВ1, ИВ2, ИВ3. Пример схемного
обозначения КМ555 ИВ1 приведен на рис.
17.7б. Управляющий сигнал "0". Поэтому
все входы и выходы схемы инверсные.
Вход
![]() - управляющий. Если на этом входе
присутствует логическая "1", то
все входы закрыты. Выходы
- управляющий. Если на этом входе
присутствует логическая "1", то
все входы закрыты. Выходы
![]() и
и
![]() - контрольные. Они выдают информацию о
состоянии схемы в данный момент.
- контрольные. Они выдают информацию о
состоянии схемы в данный момент.
Дешифраторы предназначены для преобразования цифровой информации из двоичной системы счисления в десятичную. Для примера рассмотрим принцип построения схемы преобразования кода 8-4-2-1 в цифры. У такой схемы четыре входа (по числу цифр). В зависимости от вида кодовой комбинации на входе сигнал «1» появится только на одном определенном выходе.
Из приведенного словесного описания следует, что дешифратор выполняет преобразование, обратное шифратору. Этому описанию соответствует комбинированная таблица 17.2. только входные и выходные сигналы меняются местами. Для построения схемы от таблицы 17.2 нужно перейти к алгебраическому выражению, применив в минимизацию с помощью карт Карно.
Для четырехразрядного кода карта Карно должна иметь 16 квадратов. Таблицей 17.2 заданы значения (определены) только 10 комбинаций. Значит, для шести квадратов функция не определена и их заполняют индексом «Х». В процессе минимизации вместо «Х» можно рассматривать «1», что значительно упрощает работу.
Дешифратор имеет 10 выходов. Значит, нужно сформировать десять функций F. В общем, для каждой функции нужна своя карта Карно. Но в данном случае можно воспользоваться одной картой для всех десяти функций. На рис. 17.8 а и 17.8 б приведены карты Карно для функций F0 и F8, а на рис. 17.8 в – обобщенная карта Карно. На ней контур каждой функции обозначен

соответствующей цифрой. На основании минимизации получаем следующие алгебраические выражения для функций дешифратора:
|
|
|
Используя выражения (17.7) можно построить схему дешифратора на элементах "НЕ" и "И". Но на практик6е такую схему чаще выполняют на элементах "НЕ" и "И-НЕ". При этом только на дешифрованном выходе будет уровень логического нуля (транзистор открыт), а на остальных выходах – уровень логической "1" (транзистор закрыт). Такая схема потребляет меньшую мощность.
В микросхемном исполнении дешифраторы
выпускаются в составе всех серий
цифровых интегральных микросхем,
например К155 ИД1, КМ555 ИД18, 530 ИД14 и др.
Условное графическое обозначение
микросхемы К155 ИД3 приведено на рис.
17.9. Этот дешифратор имеет 4 входа и 16
выходов. Входы
микросхемном исполнении дешифраторы
выпускаются в составе всех серий
цифровых интегральных микросхем,
например К155 ИД1, КМ555 ИД18, 530 ИД14 и др.
Условное графическое обозначение
микросхемы К155 ИД3 приведено на рис.
17.9. Этот дешифратор имеет 4 входа и 16
выходов. Входы
![]() и
и
![]() - управляющие. Преобразование
осуществляется только при низком уровне
на обоих управляющих входах.
- управляющие. Преобразование
осуществляется только при низком уровне
на обоих управляющих входах.
Преобразователи кодов (ПК) предназначены для преобразования одного двоичного кода в другой, например кода Грея в код 8-4-2-1. Принцип построения ПК аналогичен принципу построения шифраторов и дешифраторов. В микросхемном исполнении ПК обозначают индексами ПР.
Мультиплексоры и демультиплексоры образуют группу коммутаторов. Они служат для избирательного переключения сигналов (каналов). Мультиплексоры передают один из "n" входных сигналов на выход устройства. Номер выбранного входа задается адресными сигналами (рис. 17.9а). Например, трехзарядный адресный сигнал может управлять переключением восьми входов.
Демультиплексор (рис. 17.9б) передает входной (цифровой) сигнал на один из "n" выходов. Номер выхода задается адресными сигналами.
С умматоры
предназначены для выполнения
арифметических действий с двоичными
числами: сложения, вычитания, умножения
и деления – и относятся к арифметическим
устройствам. Арифметические устройства
воспринимают переменные "0" и "1"
как цифры и выполняет действия над ними
по законам двоичной арифметики:
умматоры
предназначены для выполнения
арифметических действий с двоичными
числами: сложения, вычитания, умножения
и деления – и относятся к арифметическим
устройствам. Арифметические устройства
воспринимают переменные "0" и "1"
как цифры и выполняет действия над ними
по законам двоичной арифметики:
![]()
![]() (17.8)
(17.8)
В (17.8) последнее действие предполагает, что "1" переносится в старший разряд. Такие действия реализует логическая ячейка "исключающее ИЛИ". Ее схемное обозначение имеет вид:
З десь
десь
![]() и
и![]() - i-е разряды складываемых
чисел,
- i-е разряды складываемых
чисел,
![]() - сумма.
- сумма.
Суммирование
двоичных чисел выполняется поразрядно,
от младшего разряда к старшему. Сумма
может быть записана одним числом -
![]() (т.е. "0" или "1") или двумя -
(т.е. "0" или "1") или двумя -
![]() .
Функция Р называется переносом в
старший разряд.
.
Функция Р называется переносом в
старший разряд.
Пример: Выполним сложение двух цифр: 7 + 5
![]()
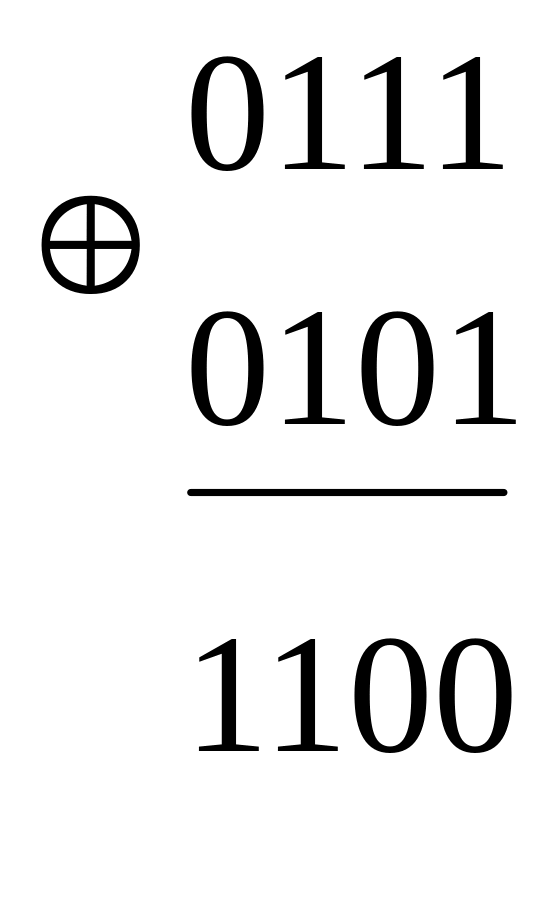
Важнейшая из
арифметических операций – сложение.
Вычитание – это сложение, в котором
вычитаемое вводится в дополнительном
коде. Дополнительный код образуется
как разность
![]() .
Например, цифра 7 в прямом коде имеет
вид 0111. Ее дополнительный код образуется
как разность 16 – 7 = 9, т. е . 1001. Тогда:
.
Например, цифра 7 в прямом коде имеет
вид 0111. Ее дополнительный код образуется
как разность 16 – 7 = 9, т. е . 1001. Тогда:
![]()
 .
Или
.
Или
![]()
 ;
;
![]()

Переносом старшего разряда пренебрегают. Умножение и деление могут выполняться как последовательное сложение и вычитание.
В зависимости от способа обработки чисел сумматоры могут быть последовательного или параллельного типа. В последовательных сумматорах сложение чисел производится поразрядно, последовательно во времени. В сумматорах параллельного типа сложение всех разрядов происходит одновременно.
Простейшим суммирующим элементом является одноразрядный полусумматор. Он имеет два входа – А и В для двух слагаемых и два выхода: S и P (Рис. 17.10а). Полусумматор обозначается буквами HS (half-sum). Таблица истинности полусумматора приведена на рис. 17.10б.
|
Входы
Выходы
A
B
S
P
0
0
0
0
1
0
1
0
0
1
1
0
1
1
0
1
б) |
|
||||||||||||||||||||||||
Рис. 17.10
Таблица истинности (рис. 17.10б) показывает, что функция S полностью совпадает с действиями (17.8). Поэтому можно записать:
![]()
№
Входы
Выходы
Ai
Bi
Pi
Si
Pi+1
0
0
0
0
0
0
1
0
0
1
1
0
2
0
1
0
1
0
3
0
1
1
0
1
4
1
0
0
1
0
5
1
0
1
0
1
6
1
1
0
0
1
7
1
1
1
1
1
|
б) |
в |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Рис. 17.11
Функция
![]() .
От сюда следует, что в состав полусумматора
должны входить два элемента: "исключающее
ИЛИ" и "И" (рис. 17.10в).
.
От сюда следует, что в состав полусумматора
должны входить два элемента: "исключающее
ИЛИ" и "И" (рис. 17.10в).
Полный одноразрядный сумматор имеет три входа и два выхода (рис. 17.11а). На третий вход подается результат переноса предыдущего сумматора. На рис. 17.11б приведена таблица истинности сумматора. Схема одноразрядного сумматора содержит два полусумматора и элемент ИЛИ (см. рис. 17.11в).
Н а
рис. 17.12а приведена схема четырех
разрядного параллельного сумматора с
последовательным переносом. Число
сумматоров равно числу разрядов. Выход
переноса каждого предыдущего сумматора
соединен со входом переноса последующего
сумматора. Вход переноса сумматора
первого разряда заземлен (установлен
логический "0"). Слагаемые
а
рис. 17.12а приведена схема четырех
разрядного параллельного сумматора с
последовательным переносом. Число
сумматоров равно числу разрядов. Выход
переноса каждого предыдущего сумматора
соединен со входом переноса последующего
сумматора. Вход переноса сумматора
первого разряда заземлен (установлен
логический "0"). Слагаемые
![]() и
и
![]() складываются во всех разрядах
одновременно, а перенос
складываются во всех разрядах
одновременно, а перенос
![]() поступает с окончанием сложения в
предыдущем разряде
поступает с окончанием сложения в
предыдущем разряде
![]() .
.
Сумматоры
выпускаются в виде готовых изделий в
составе многих серий цифровых микросхем.
Например, К155 ИМ3 – четырехразрядный
параллельный сумматор (рис. 17.12б). Вход
переноса
![]() имеется только у младшего разряда, а
выход только у старшего (
имеется только у младшего разряда, а
выход только у старшего (![]() ).
Это позволяет наращивать микросхемы
и использовать их для выполнения
различных арифметических операций.
).
Это позволяет наращивать микросхемы
и использовать их для выполнения
различных арифметических операций.
Цифровые
компараторы предназначены для
сравнения двух чисел, заданных в двоичном
коде одинаковой разрядности. Компараторы
определяют равенство чисел, т. е. А =
В, и неравенство, т. е. A
> B или A
< B, и имеют три
выхода и
![]() входа. Выпускаются цифровые компараторы
в виде готовых микросхем, например К555
СП1 – четырехразрядный компаратор.
входа. Выпускаются цифровые компараторы
в виде готовых микросхем, например К555
СП1 – четырехразрядный компаратор.




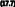



 )
)