
- •1. Законы Кирхгофа. Запись законов Кирхгофа в матричной форме.
- •2. Закон Ома для обобщенной ветви.
- •4. Метод узловых потенциалов. Запись узловых уравнении в матричной форме.
- •5. Баланс мощностей в цепи постоянного тока.
- •6. Метод эквивалентного генератора.
- •8. Взаимное преобразование реальных источников эдс и тока.
- •15. Векторные и топографические диаграммы.
- •16. Мощность в цепи синусоидального тока. Активная, реактивная, полная, комплексная мощности.
- •17. Баланс мощностей в цепи синусоидального тока.
- •18. Коэффициент мощности.
- •21. Трансформатор с линейной характеристикой. Входное сопротивление. Векторная диаграмма.
- •3. Метод контурных токов. Запись контурных уравнении в матричной форме.
- •Метод контурных токов в матричной форме
- •26. Резонанс напряжений. Резонансная частота. Добротность.
- •Резонанс в цепи с последовательно соединенными элементами (резонанс напряжений)
- •29. Резонанс токов. Резонансная частота.
- •32. Расчет трехфазной цепи
- •Расчет симметричных режимов работы трехфазных систем
- •Расчет несимметричных режимов работы трехфазных систем
- •39. Фильтр напряжений обратной последовательности
- •Характеристическое сопротивление и коэффициент распространения симметричного четырехполюсника
1. Законы Кирхгофа. Запись законов Кирхгофа в матричной форме.
1-ый закон Кирхгофа:
Алгебраическая сумма токов в узле электрической цепи равна 0 в любой момент времени. Сумма токов, втекающих в узел, равна сумме токов, вытекающих из этого узла.
Узловая матрица Aн =a[i,j], определяется следующим образом: строчками являются узлы схемы, а столбцами соответствующие ветви.
ai,j=0, если j-ая ветвь не подсоединена к i-ому узлу.
ai,j= +(-) 1, если j-ая ветвь подсоединена к узлу и направлена от узла (к узлу).
Запишем 1-ый з-н Кирхгофа с помощью матрицы:
Ан*iв
=0 iв=
 - матрица столбец тока ветвей.
- матрица столбец тока ветвей.
Система алгебраических ур-ний, соответствующая матричному, является системой зависимых ур-ний, т.к. любые ур-ния являются комбинацией других. Для получения линейно независимых ур-ний, один из узлов принимается за базовый, т.е. его потенциал равен нулю, тогда узловая матрица составляется для всех узлов кроме базового
А=
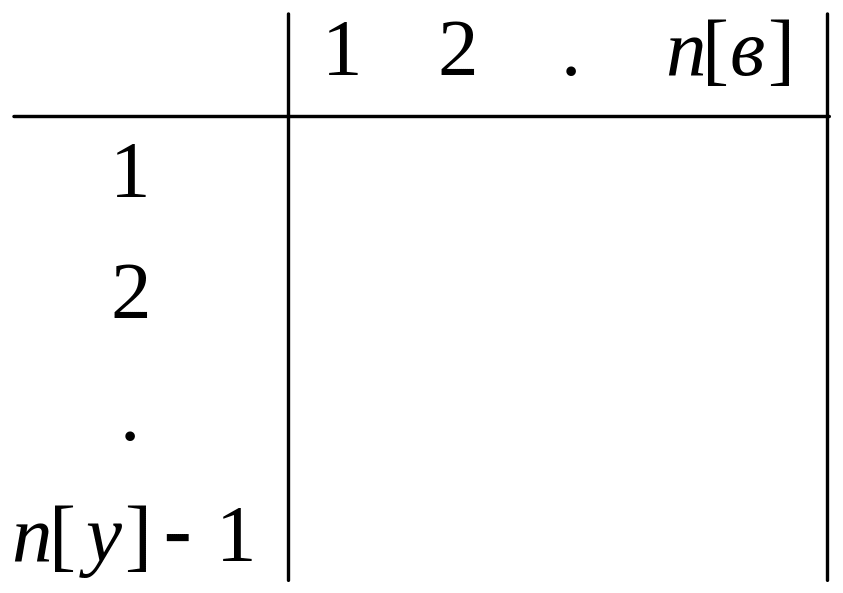 => 1-ый закон Кирхгофа :
Aн*iв
=0
=> 1-ый закон Кирхгофа :
Aн*iв
=0
2-ой закон Кирхгофа:
Алгебраическая сумма напряжений в замкнутом контуре электрической цепи равна 0 в любой момент времени. Сумма падений напряжений в контуре равна сумме ЭДС в этом контуре.
Контурная матрица В =bi,j определяется следующим образом: строчками являются главные контура, а столбцами ветви.
bi,j = 0, если j-ветвь не входит в i-й контур.
bi,j= +(-), если j-ветвь входит в i-й контур и направление ветви совпадает с направлением контура. Направление контура выбираем по направлению ветви связи (если направлено противоположно)
Запишем с помощью матрицы В 2-ой закон Кирхгофа: В* U в=0 (система линейно независимых уравнений)
2. Закон Ома для обобщенной ветви.
U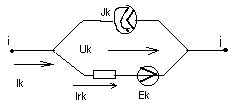 rk=i*rk*rk
Ue=ek
rk=i*rk*rk
Ue=ek
Найдем зависимость напряжения и тока
1-й закон Кирхгофа: Ik=Ir k - Jk
Ir k=(Uk-Ek)*gk, gk=1/(rk)
Ik=(Uk+Ek)*gk-Jk - закон Ома для обобщенной ветви
Напишем то же для напряжения:
Uk=(Ik+Jk)*Rk-Ek – обобщенный закон Ома для напряжения обобщенной ветви.
4. Метод узловых потенциалов. Запись узловых уравнении в матричной форме.
Д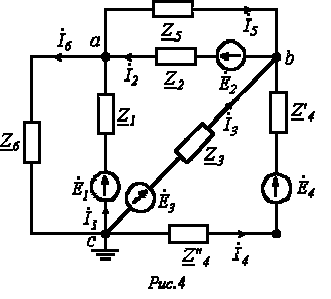 анный
метод вытекает из первого закона
Кирхгофа. В качестве неизвестных
принимаются потенциалы узлов, по
найденным значениям которых с помощью
закона Ома для участка цепи с источником
ЭДС затем находят токи в ветвях. Поскольку
потенциал – величина относительная,
потенциал одного из узлов (любого)
принимается равным нулю. Таким образом,
число неизвестных потенциалов, а
следовательно, и число уравнений равно
анный
метод вытекает из первого закона
Кирхгофа. В качестве неизвестных
принимаются потенциалы узлов, по
найденным значениям которых с помощью
закона Ома для участка цепи с источником
ЭДС затем находят токи в ветвях. Поскольку
потенциал – величина относительная,
потенциал одного из узлов (любого)
принимается равным нулю. Таким образом,
число неизвестных потенциалов, а
следовательно, и число уравнений равно
![]() ,
т.е. числу ветвей дерева
,
т.е. числу ветвей дерева
![]() .
.
Пусть
имеем схему по рис. 4, в которой примем
![]() .
.
Д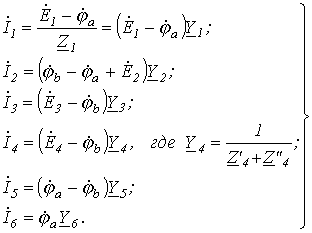 опустим,
что
опустим,
что
![]() и
и
![]() известны.
Тогда значения токов на основании закона
Ома для участка цепи с источником ЭДС
известны.
Тогда значения токов на основании закона
Ома для участка цепи с источником ЭДС
Запишем
уравнение по первому закону Кирхгофа
для узла а:
![]()
и подставим значения входящих в него токов, определенных выше:
![]() .
.
Сгруппировав соответствующие члены, получим:
![]() .
.
Аналогично можно записать для узла b:
![]() .
.
Как и по методу контурных токов, система уравнений по методу узловых потенциалов может быть составлена формальным путем. При этом необходимо руководствоваться следующими правилами:
1.
В левой части i-го
уравнения
записывается со знаком “+”потенциал
![]() i-го
узла, для которого составляется данное
i-е
уравнение, умноженный на сумму
проводимостей
i-го
узла, для которого составляется данное
i-е
уравнение, умноженный на сумму
проводимостей
![]() ветвей,
присоединенных к данному i-му
узлу, и со знаком “-”потенциал
ветвей,
присоединенных к данному i-му
узлу, и со знаком “-”потенциал
![]() соседних
узлов, каждый из которых умножен на
сумму проводимостей
соседних
узлов, каждый из которых умножен на
сумму проводимостей
![]() ветвей,
присоединенных к i-му
и
k-му
узлам.
ветвей,
присоединенных к i-му
и
k-му
узлам.
Из
сказанного следует, что все члены
![]() ,
стоящие на главной диагонали в левой
части системы уравнений, записываются
со знаком “+”, а все остальные – со
знаком “-”, причем
,
стоящие на главной диагонали в левой
части системы уравнений, записываются
со знаком “+”, а все остальные – со
знаком “-”, причем
![]() .
Последнее равенство по аналогии с
методом контурных токов обеспечивает
симметрию коэффициентов уравнений
относительно главной диагонали.
.
Последнее равенство по аналогии с
методом контурных токов обеспечивает
симметрию коэффициентов уравнений
относительно главной диагонали.
2.
В правой части i-го
уравнения
записывается так называемый узловой
ток
![]() ,
равный сумме произведений ЭДС ветвей,
подходящих к i-му
узлу, и проводимостей этих ветвей. При
этом член суммы записывается со знаком
“+”, если соответствующая ЭДС направлена
к i-му
узлу, в противном случае ставится знак
“-”. Если в подходящих к i-му
узлу ветвях содержатся источники тока,
то знаки токов источников токов, входящих
в узловой ток простыми слагаемыми,
определяются аналогично.
,
равный сумме произведений ЭДС ветвей,
подходящих к i-му
узлу, и проводимостей этих ветвей. При
этом член суммы записывается со знаком
“+”, если соответствующая ЭДС направлена
к i-му
узлу, в противном случае ставится знак
“-”. Если в подходящих к i-му
узлу ветвях содержатся источники тока,
то знаки токов источников токов, входящих
в узловой ток простыми слагаемыми,
определяются аналогично.
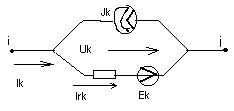
Ir k=(URk)/Rk=URk*gk; где gk=1/Rk- проводимость
IRk=(Uk+Ek)/Rk=(i-j-Ek)/Rk ;
A
* I![]() =0
(1 закон
Кирхгофа);
=0
(1 закон
Кирхгофа);
IB=GB*URB-JB=GB*(UB + EB)-JB ; UR= UB + EB
A *GB*UB+ A *GB*EB- A *JB=0 ;
UB=AT*=GB*(AT*+ EB)- JB домножим на A
A * IB = A *GB* A T*+ A *GB*EB- A *JB
В-ветви;
У-узлы;
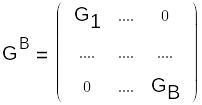
![]() G
G![]() *=J
*=J
![]() узловое
уравнение в матричном виде.
узловое
уравнение в матричном виде.
![]()
Замечание: Метод узловых потенциалов справедлив для схем в которых отсутствуют схемы с проводимостью равной нулю, т.е. нет короткозамкнутых цепей (gi=, т.е. ri=0)
Число ур-ний ny-1<nB
