41. Параллельная схема идентификации с нулевой передачей знаний.

Идентификация - присвоение субъектам и объектам идентификатора и / или сравнение идентификатора с перечнем присвоенных идентификаторов. Центром распределения ключей формируется последовательность ключей: V=V₁,V₂,…,V_R; S=S₁,S₂,…,S_R; 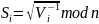; значение К – задает степень параллелизма. Ход алгоритма:1) A:r<n, где r-случайное число; AB: x=r²mod n 2) BA: d1,b2,…,bi; 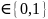; 3)A:y=r*(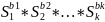 ) mod n; AB:y 4) B:x=y²*(V^b1₁* V^b2₂*…* V^bk_k)mod n; И так пока верификатор не будет уверен что абонент знает кто он есть. Вероятность нарушения безопасности: Рпод=1/2^kt. При использовании интеллектуальной карты можно изменять количество итераций и степень распараллеливания протоколов идентификации.

42. Требования к протоколам электронного тайного голосования. Пример протокола голосования.

Рассмотрим протокол электронного голосования, использующий асимметричную криптографию и протокол привязки к биту. Задача ставится следующим образом : участниками протокола являются m лиц с правом голоса и n счетных комиссий, которые создаются для обеспечения анонимности и предотвращения фальсификации итогов голосования. Требуется таким образом организовать голосование, чтобы выполнялись следующие условия: голосуют только уполномоченные избиратели; любой участник имеет право отдать не более одного голоса; ни один из участников не может узнать, как проголосовал другой; никто не может дублировать чужой голос; конечный результат будет подсчитан корректно; любой участник может проверить правильность результата; протокол должен работать и в случае, если некоторые из участников ведут себя нечестно. Рассмотрим протокол, предложенный в 1996 г. Сначала каждая комиссия получает открытый ключ, а каждый голосующий – цифровую подпись. Пусть p – простое число,  - элемент поля Zp, имеющий порядок q, <> - элемент, для которого нахождение значения log_ является трудной задачей. Будем использовать схему битовых обязательств с функцией f(,x)= ^x^a. Пошаговое выполнение протокола голосования осуществляется следующим образом: 1.Заполнение бюллетеня избирателями. Пусть j-й избиратель выбирает голос a_j{-1,1} и случайный элемент r_jZq. Затем он публикует свидетельство _0j=^rj^aj, 1≤j≤m. В результате в общем доступе будут свидетельства всех участников ₀₁,…, _0m. Кроме того, j-й избиратель выполняет автономную версию протокола доказательства знания. Далее j-й избиратель подписывает свой голос и докузательство своей цифровой подписью. 2.Передача бюллетеней в комиссии. Для передачи бюллетеней с голосами избирателей счетным комиссия используется пороговая схема разделения секрета Шамира: j-й избиратель выбирает два многочлена над полем Zq степени t<n (первый – для голосов, второй – для затемняющих факторов): A_j(x)=a_j+a_1jx+...+a_tjx_t, R_j(x)=r_j+r_1jx+...+r_tjx^t, Значения которых в точках 1,…,n будут являться долями секрета (u_ij,w_ij)=(A_j(i),R_j(i)), i=1,n. Далее j-й избиратель шифрует доли (u_ij,w_ij) на открытом ключе i-й комиссии и отправляет эти значения в i-ю комиссию. Помимо этого j-й избиратель передает i-й счетной комиссии сам многочлен A_j(x), регистрируя с помощью той же схемы битовых обязательств его коэффициенты f(a_1j,r_lj)=α^r_ljβ^a_lj, 1≤l≤t. Подсчет голосов: Каждая i-я комиссия подсчитывает бюллетени, публикует результат подсчета бюллетеней 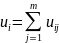, а также обнародует сумму затемняющих факторов 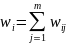. Теперь каждый участник (комиссия и избиратель) может убедиться в корректности опубликованных данных, проверив равенство: 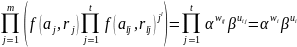. Для определения итога голосования берем t значений u_i, которые также являются значениями некоторого многочлена в точке i, так как 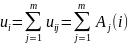, и интерполируем по ним результат . 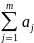Если результат – отрицательное число, то голосов, равных -1, больше, если – положительное, то больше голосов, равных +1. Далее проверяют, выполняются ли приведенные выше семь условий.