
- •1. Основные понятия криптографии
- •2. Принципы построения симметричных блочных шифров.
- •3. Математическая модель блочного шифра.
- •4. Классификация блочных шифров.
- •5. Основные виды примитивов блочных алгоритмов шифрования.
- •6. Структура стандарта шифрования данных гост 28147-89.
- •7. Основные параметры алгоритма гост 28147-89, его достоинства и недостатки.
- •8. Режимы использования алгоритма гост 28147-89.
- •9. Структура и основные параметры алгоритма шифрования des, его достоинства и недостатки.
- •10,11,12. Режимы применения блочных шифров.
- •13. Системы с открытым ключом, основанные на сложности разложения целых чисел.
- •14. Системы с открытым ключом, основанные на сложности дискретного логарифмирования
- •15. Основные понятия и определение криптографического протокола.
- •16. Требования, предъявляемые к криптографическим протоколам.
- •17. Типы атак на криптографические протоколы
- •18. Формальные методы анализа криптографических протоколов.
- •19. Общие сведения об обеспечении целостности информации
- •20. Применение циклических кодов (crc) для обеспечения целостности информации
- •21. Обобщенная схема формирования кодов аутинтификации сообщений (mac - кодов). Достоинства и недостатки мас – кадов
- •22.Коды обнаружения манипуляций с данными (mdc - коды), их достоинства и недостатки.
- •23.Простейшая схема аутентификации субъектов с использованием пароля.
- •2 4. Схема симметричной аутентификации с третьей доверенной стороной.
- •25. Ассиметричные методы аутинтификации
- •26. Принципы генерации и хранения криптографических ключей.
- •27. Функции управления ключами
- •28. Протоколы распределения ключей на основе применения асимметричных криптосистем. Протокол Диффи-Хелмана.
- •30. Алгоритм хэширования md 5, структура, достоинства и недостатки.
- •31. Алгоритмы хэширования sha-1,2 , структура, достоинства и недостатки.
- •34. Понятие электронной цифровой подписи (эцп) сообщения. Общие сведения об эцп.
- •35. Схема эцп на основе алгоритма с открытым ключом rsa.
- •36. Уравнения формирования и проверки эцп в соответствии с гост р 34.10-94.
- •37. Схема формирования эцп в соответствии с гост р 34.10 - 2001.
- •38. Схема проверки эцп в соответствии с гост р 34.10 - 2001.
- •39. Упрощенная схема идентификации с нулевой передачей знаний.
- •40. Параллельная схема идентификации с нулевой передачей знаний.
- •41. Параллельная схема идентификации с нулевой передачей знаний.
- •42. Требования к протоколам электронного тайного голосования. Пример протокола голосования.
36. Уравнения формирования и проверки эцп в соответствии с гост р 34.10-94.
ЭЦП - реквизит электронного документа, позволяющий установить отсутствие искажения информации в электронном документе с момента формирования ЭЦП и проверить принадлежность подписи владельцу сертификата ключа ЭЦП. Значение реквизита получается в результате криптографического преобразования информации с использованием закрытого ключа ЭЦП.
p – простое число (510<=p<=512 или 1022<=p<=1024); q – простой делитель числа p-1, 2255<=p<=2256; a – число, относящееся к показателю q по модулю p. Секретный ключ – случайное число х, 1<x<q. Формирование открытого ключа y=axmod p. Вычисление подписи к сообщению m: 1. Случайное число k, 1<k<q; 2. r=(ak mod p)mod q – 1 первая часть подписи; 3. Хэш-функция: E=H(m); 4. s=kE+xr mod q (s!=0) – вторая часть подписи. Проверка подписи: 1. r<q и s<q 2. E=H(m); w=E-1mod q, если E!=0 и w=1, если E=0. 4. u=sw mod q и v=-rw mod q; 5. ru’=(auyvmod p)mod q; Если r=r’ – проверка положительна.
37. Схема формирования эцп в соответствии с гост р 34.10 - 2001.
Электронная
цифровая подпись
(ЭЦП) -
реквизит электронного документа,
позволяющий установить отсутствие
искажения информации в электронном
документе с момента формирования ЭЦП
и проверить принадлежность подписи
владельцу сертификата ключа ЭЦП.
Значение реквизита получается в
результате криптографического
преобразования информации с использованием
закрытого
ключа ЭЦП.
Для получения цифровой подписи под
сообщением
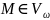 необходимо выполнить следующие действия
(шаги): Шаг
1
- вычислить хэш-код сообщения
необходимо выполнить следующие действия
(шаги): Шаг
1
- вычислить хэш-код сообщения
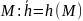 Шаг
2
- вычислить целое число а, двоичным
представлением которого является вектор
Шаг
2
- вычислить целое число а, двоичным
представлением которого является вектор
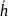 ,
и определить
,
и определить
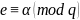 Если
е
=
0, то определить е
=
1. Шаг
3
- сгенерировать случайное (псевдослучайное)
целое число k
,
удовлетворяющее неравенству 0 < k
<
q
.
Шаг
4
- вычислить точку эллиптической кривой
C
= kP и
определить
Если
е
=
0, то определить е
=
1. Шаг
3
- сгенерировать случайное (псевдослучайное)
целое число k
,
удовлетворяющее неравенству 0 < k
<
q
.
Шаг
4
- вычислить точку эллиптической кривой
C
= kP и
определить
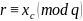 где
xc-x
- координата точки С
.
Если r
=
0, то вернуться к шагу 3. Шаг
5
- вычислить значение
где
xc-x
- координата точки С
.
Если r
=
0, то вернуться к шагу 3. Шаг
5
- вычислить значение
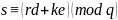 Если
s
=
0, то вернуться к шагу 3. Шаг
6
- вычислить двоичные векторы
Если
s
=
0, то вернуться к шагу 3. Шаг
6
- вычислить двоичные векторы
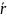 и
и
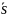 ,
соответствующие r
и
s
,
и определить цифровую подпись
,
соответствующие r
и
s
,
и определить цифровую подпись
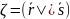 как
конкатенацию двух двоичных векторов.
Исходными данными этого процесса
являются ключ подписи d
и
подписываемое сообщение М
,
а выходным результатом - цифровая подпись
как
конкатенацию двух двоичных векторов.
Исходными данными этого процесса
являются ключ подписи d
и
подписываемое сообщение М
,
а выходным результатом - цифровая подпись
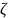 .
.
38. Схема проверки эцп в соответствии с гост р 34.10 - 2001.
Электронная
цифровая подпись
(ЭЦП) -
реквизит электронного документа,
позволяющий установить отсутствие
искажения информации в электронном
документе с момента формирования ЭЦП
и проверить принадлежность подписи
владельцу сертификата ключа ЭЦП.
Значение реквизита получается в
результате криптографического
преобразования информации с использованием
закрытого
ключа ЭЦП.
Для проверки цифровой подписи
, под полученным сообщением М
необходимо
выполнить следующие действия (шаги):
Шаг
1
- по полученной подписи
вычислить целые числа r
и
s
.
Если выполнены неравенства 0 <
r < q, 0
<
s < q ,
то перейти к следующему шагу. В противном
случае подпись неверна. Шаг
2
- вычислить хэш-код полученного сообщения
М:
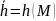 Шаг
3
- вычислить целое число
Шаг
3
- вычислить целое число
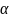 ,
двоичным представлением которого
является вектор
,
и определить
,
двоичным представлением которого
является вектор
,
и определить
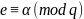 Если е
=
0, то определить е
=
1. Шаг
4
- вычислить значение
Если е
=
0, то определить е
=
1. Шаг
4
- вычислить значение
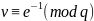 Шаг
5
- вычислить значения
Шаг
5
- вычислить значения
 Шаг
6
- вычислить точку эллиптической кривой
Шаг
6
- вычислить точку эллиптической кривой
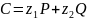 и определить
и определить
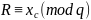 где xc-x
- координата точки С
.
Шаг
7
- если выполнено равенство R
= r ,
то подпись принимается, в противном
случае, подпись неверна. Исходными
данными этого процесса являются
подписанное сообщение М,
цифровая подпись
,
и ключ проверки Q,
а выходным результатом - свидетельство
о достоверности или ошибочности данной
подписи.
где xc-x
- координата точки С
.
Шаг
7
- если выполнено равенство R
= r ,
то подпись принимается, в противном
случае, подпись неверна. Исходными
данными этого процесса являются
подписанное сообщение М,
цифровая подпись
,
и ключ проверки Q,
а выходным результатом - свидетельство
о достоверности или ошибочности данной
подписи.
