28. Протоколы распределения ключей на основе применения асимметричных криптосистем. Протокол Диффи-Хелмана.

В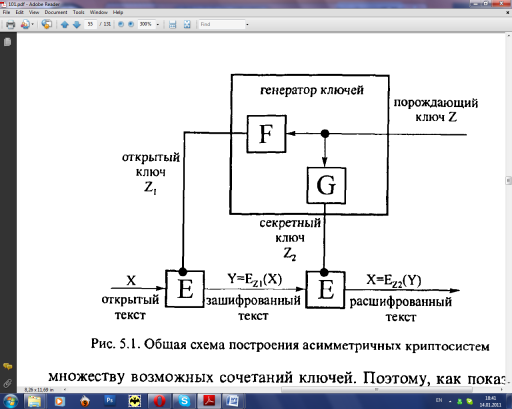 современных телекоммуникационных сетях с большим количеством пользователей часто возникают ситуации, связанные с невозможностью доверия друг другу. Принципиально новое, что вносится асимметричными криптосистемами – возможность построения криптографических протоколов, решающих задачи взаимодействия не доверяющих друг другу сторон. Секретная связь осуществляется только в одном направлении, отсюда и название криптосистем – ассиметричные. 1й ключ – открытый, может быть опубликован для шифрования данных всеми пользователями. 2й ключ – секретный, используется только получателем для расшифрования. Особенности таких систем: наличие связанных между собой ключей для шифрования и расшифрования, каждый из которых не может быть получен из другого с приемлемыми вычислительными и временными затратами; для организации безопасной связи не требуется передача секретного ключа. Картинка: Открытый и секретный ключ формируются генераторами F и G по порождающему ключу, выбираемому случайным образом. Получатель оставляет у себя Z2 и высылает Z1 отправителю, который, применяя этот ключ, может зашифровать сообщение и отправить получателю. Шифрование E выполняется с помощью Z1, расшифрование – с помощью Z2. Наиболее распространенные протоколы такого вида: RSA (Rivest-Shamir-Adleman, Ривест — Шамир — Адлеман), DSA (Digital Signature Algorithm), Elgamal (Шифросистема Эль-Гамаля), Diffie-Hellman (Обмен ключами Диффи — Хелмана), ECC (Elliptic Curve Cryptography, криптография эллиптической кривой), ГОСТ Р 34.10-2001 и др.

Алгори́тм Ди́ффи — Хе́ллмана — алгоритм, позволяющий двум сторонам получить общий секретный ключ, используя незащищенный от прослушивания, но защищённый от подмены, канал связи. Предположим, что обоим абонентам известны некоторые два числа g и p (например, они могут быть «зашиты» в программное обеспечение), которые не являются секретными и могут быть известны также другим заинтересованным лицам. Для того, чтобы создать неизвестный более никому секретный ключ, оба абонента генерируют большие случайные числа: первый абонент — число a, второй абонент — число b. Затем первый абонент вычисляет значение A = g^a mod p и пересылает его второму, а второй вычисляет B = g^b mod p и передаёт первому. Предполагается, что злоумышленник может получить оба этих значения, но не модифицировать их (то есть у него нет возможности вмешаться в процесс передачи). На втором этапе, первый абонент на основе имеющегося у него a и полученного по сети B вычисляет значение B^a mod p = g^ab mod p, а второй абонент на основе имеющегося у него b и полученного по сети A вычисляет значение A^b mod p = g^ab mod p. Как нетрудно видеть, у обоих абонентов получилось одно и то же число: K = g^ab mod p. Его они и могут использовать в качестве секретного ключа, поскольку здесь злоумышленник встретится с практически неразрешимой (за разумное время) проблемой вычисления g^ab mod p по перехваченным g^a mod p и g^b mod p, если числа p,a,b выбраны достаточно большими. Криптографическая стойкость алгоритма Диффи — Хеллмана (то есть сложность вычисления K=g^ab mod p по известным p, g, A=g^a mod p и B=g^b mod p), основана на предполагаемой сложности проблемы дискретного логарифмирования, и работает он только на линиях связи, надёжно защищённых от модификации.

29.Хэш-функции сообщений. Общие принципы построения, требования, предъявляемые к ним.

Основы построения хэш-функций.Общепринятым принципом построения хэш-функций является итеративная последовательная схема. По этой методики ядром алгоритма является преобразование k бит в n бит. Величина n - разрядность результата хэш-функции, а k - произвольное число, большее n. Базовое преобразование должно обладать всеми свойствами хэш-функции т.е. необратимостью и невозможностью инвариантного изменения входных данных. Хэширование производится с помощью промежуточной вспомогательной переменной разрядностью в n бит. В качестве ее начального значения выбирается произвольное известное всем сторонам значение, например, 0. Входные данные разбиваются на блоки по (k-n) бит. На каждой итерации хэширования со значением промежуточной величины, полученной на предыдущей итерации, объединяется очередная (k-n)-битная порция входных данных, и над получившимся k-битным блоком производится базовое преобразование. В результате весь входной текст оказывается "перемешанным" с начальным значением вспомогательной величины. Из-за характера преобразования базовую функцию часто называют сжимающей. Значение вспомогательной величины после финальной итерации поступает на выход хэш-функции (рис.2). Иногда над получившимся значением производят дополнительные преобразования. Но в том случае, если сжимающая функция спроектирована с достаточной степенью стойкости, эти преобразования излишни. При проектировании хэш-функции по итеративной схеме возникают два взаимосвязанных вопроса: как поступать с данными, не кратными числу (k-n), и как добавлять в хэш-сумму длину документа, если это требуется. Есть два варианта решения этих вопросов. В первом варианте в начало документа перед хэшированием добавляется поле фиксированной длины (например, 32 бита), в котором в двоичном виде записывается исходная длина текста. Затем объединенный блок данных дополняется нулями до ближайшего кратного (k-n) бит размера. Во втором варианте документ дополняется справа одним битом "1", а затем до кратного (k-n) бит размера битами "0". В этом варианте необходимость в поле длины отпадает - никакие два разных документа после выравнивания по границе порций не станут одинаковыми. Кроме более популярных однопроходных алгоритмов хэширования существуют и многопроходные алгоритмы. В этом случае входной блок данных на этапе расширения неоднократно повторяется, а уже затем дополняется до ближайшей границы порции.