Задача №2.214.
Найти суммарный импульс электронов в прямом проводнике длиной l=1000 м и с током I=70 А.
Решение:
Выражение для импульса:
P=mv;
v=
;
t=
Тогда получим:
v=
;
В итоге получаем,
P=I
l
.
№2.223.
Между двумя плоскими пластинами
конденсатора, отстоящими друг от друга
на расстоянии d,
находится газ. Одна из пластин эмиттирует
ежесекундно
электронов, которые, двигаясь в
электрическом поле, ионизируют молекулы
газа так, что каждый электрон создаёт
на единице длины пути α новых электронов
(и ионов). Найти электронный ток у
противоположной пластины, пренебрегая
ионизацией молекул газа ионами.
Решение:
Рассмотрим 1 электрон, который, эммитировав с пластины, прошёл путь dx.
За
это время он произведёт αdx
новых электронов, то есть заряд увеличится
в
раз.
И
так до второй пластины. В результате
заряд увеличится в
раз.
Откуда для
электронов :
Ответ:
№2.229
Ток I
течёт по тонкому проводнику, который
имеет вид правильного n-угольника,
вписанного в окружность радиуса R.
Найти магнитную индукцию в центре
данного контура. Исследовать случай
.
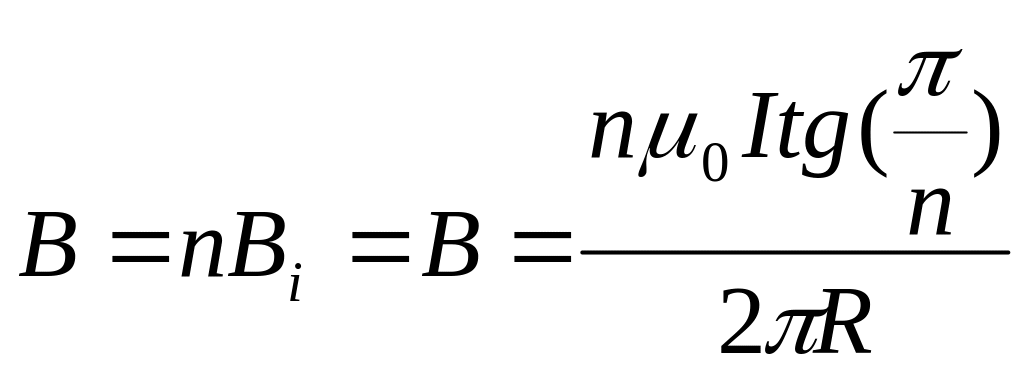
Ответ:
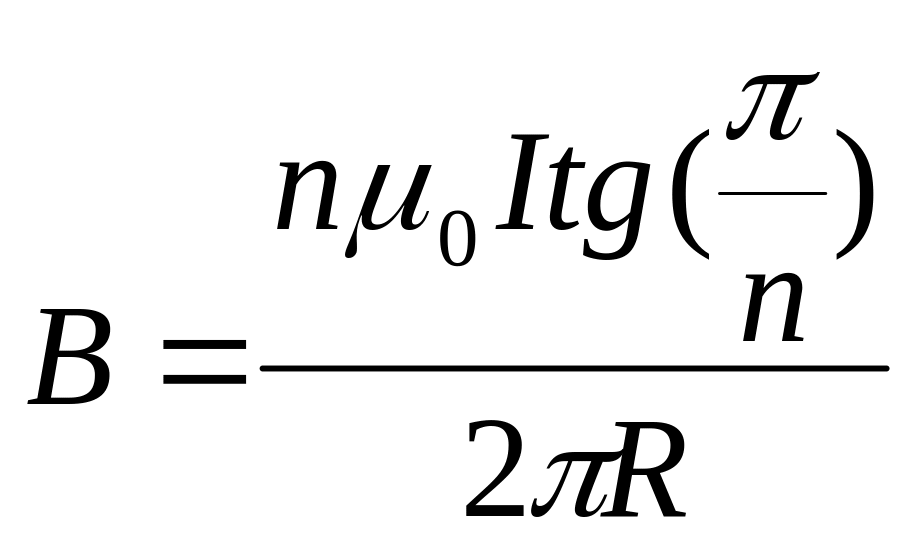при
Задача 2.230.
Найти
магнитную индукцию в центре контура,
имеющего вид прямоугольника, если его
диагональ d=16
см, угол между диагоналями =30
и ток I=5,0
A.
Решение:
По закону Био-Савара:
B=
L
; отсюда путем геометрических преобразований
получим,что L/r
=16/d
sin
,отсюда
B=
=
=
;
Ответ: B= .
2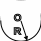
.234
Ток I=11.0A
течёт по длинному прямому проводнику,
сечение которого имеет форму тонкого
полукольца радиуса R=5.0см.
Найти индукцию магнитного поля в точке
O.
Решение:
Разобьём проводник на тонкие нити. По
каждой из них течёт ток
,
и такая нить создаёт в точке О магнитное
поле
2.242 Однородный
ток плотности
течёт внутри неограниченной пластины
толщины 2d параллельно её
поверхности. Пренебрегая влиянием
вещества пластины, найти индукцию
магнитного поля этого тока как функцию
расстояния x от средней
плоскости пластины.
Решение: copyright 2001 Андрюха, 13РФ.
Для уединённого
проводника с током
.
Элемент тока
создаёт
,
2_243 Условие: Постоянный то I течёт по длинному проводу, потом растекается радиально-симметрично по проводящей плоскости, перпендикулярной проводу. Найти индукцию магнитного поля во всех точках пространства.
Решение:
Построим цилиндр, ось которого лежит
на проводе, нижнее основание лежит в
средней плоскости проводящей плоскости.
Будем рассматривать составляющую
индукции со стороны плоскости. Каждому
элементу тока над нижним основанием
цилиндра найдётся симметричный под
основанием(они компенсируют друг друга).
Следовательно индукция поля в плоскости
основания равна нулю и поток ч/з это
основание также равен нулю. Если
вертикальные составляющие индукции на
другом основании существует, то они
направлены в одну сторону, и тогда
(4-ое уравнение Максвелла)
B=0. На боковой поверхности
индукция также равна нулю.
Получается, что в любой точке пространства составляющая индукции со стороны плоскости равна нулю. Остаётся только составляющая от провода.
Итого в полупространстве, в котором находится провод B=0I/2r.(r – расстояние от провода до данной точки) B=0 в другом полупространстве.
2.246
По прямому проводу, радиус сечения которого R, течёт постоянный ток плотности j. Пренебрегая влиянием вещества провода, найти индукцию магнитного поля этого тока в точке, положение которой относительно оси провода определяется радиусом-вектором r (перпендикулярен).
Решение:
Рассмотрим 2 случая(r<=R и r>R):
Первый: в данном случае мы рассматриваем лишь тот ток, который течет внутри “стержня” радиуса r, т.к. индукция тока во внешнем слое будет взаимно уничтожаться. Тогда:
Второй: теперь мы рассматриваем уже весь провод, а дальше по аналогии:
Ответ:
№ 2.248.
Найти плотность
тока как функцию расстояния r
от си аксиально-симметричного параллельного
потока электронов, если индукция
магнитного поля внутри потока зависит
от r как
,
где b и
-- положительные постоянные.
Р
ЕШЕНИЕ.
Запишем формулу циркуляции и закон Ампера.
Продифференцируем правую и левую части уравнения.
ОТВЕТ:
.
№2.251
У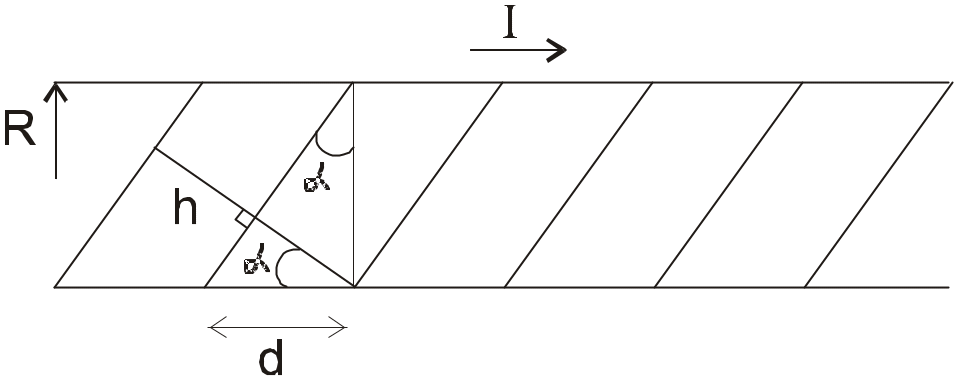
словие:
Обмоткой длинного соленоида с радиусом
сечения R=2,5
см. служит тонкая лента-проводник ширины
h=5,0
см, намотанная в один слой практически
вплотную. По ленте течет ток I=5,0
А. Найти индукцию магнитного поля внутри
и вне соленоида как функцию расстояния
r
от его оси.
Для
случая r<R:
,
где n
– плотность обмотки
n=1/d;
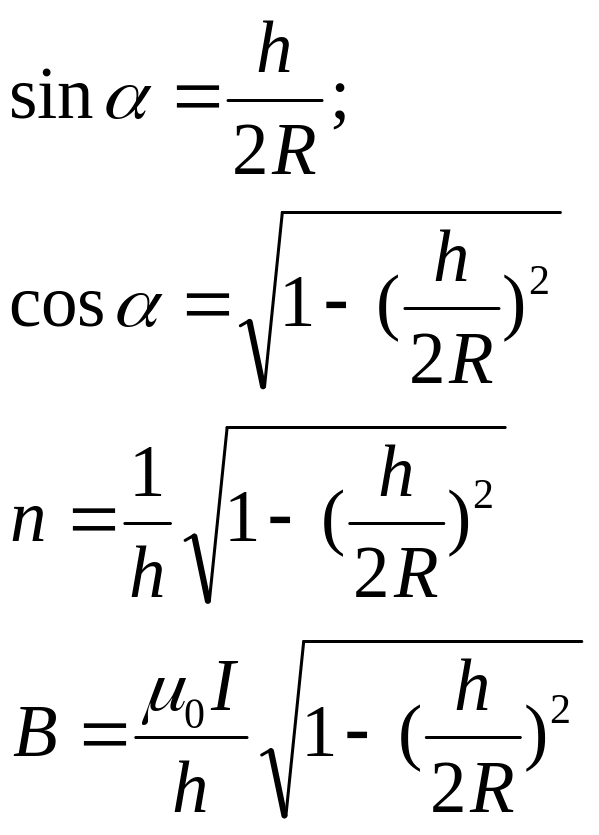
для случая r>R: по закону Ампера
№2.253
Условие:
Ток I=50 А течёт по длинному прямому проводнику круглого сечения. Пренебрегая влиянием вещества проводника, найти магнитный поток через одну из половин осевого сечения проводника в расчёте на единицу его длины.
Решение:
- плотность
тока
По
закону Ампера:
(т.к. ldr
= dS)
Ответ:
№-2.256.
Найти магнитный
момент тонкого кругового витка с током
, если радиус витка
100мм
и индукция магнитного поля в его центре
6.0мкТл.
Решение:
По определению
магнитный момент это :
; - где
площадь поверхности, ограниченной
контуром , а
-ток в контуре.
, а
;
;
Ответ:
;
2.260. Непроводящий тонкий диск радиуса R, равномерно заряженный с одной стороны с поверхностной плотностью , вращается вокруг своей оси с угловой скоростью . Найти:
а) индукцию магнитного поля в центре диска;
б) магнитный момент диска.
Решение:
Индукция поля малого движущегося заряда dq:
;
Интегрируем по поверхности диска
Ответ:
№ 2.264
Два протона движутся параллельно друг другу с одинаковой скоростью v=300 км/c.Найти отношение сил магнитного и электрического взаимодействия данных протонов.
Решение:
Электрическое
взаимодействие
;
Магнитное
(элемент тока равен ev)
;
Ответ : .
Задача 2.267 Катушка с током I=10мА поместили в однородное магнитное поле так, что ее ось совпала с направлением поля. Обмотка катушки однослойная из медного провода диаметром d=0,10мм, радиус витков R=30мм. При каком значении индукции внешнего поля обмотка катушки может быть разорвана?
Решение:
Сила ,которую может выдержать катушка равнва F=S, где предел прочности для меди .
С другой стороны на катушку действует сила Ампера F=BIL, приравнивая силы получаем:
S=BIL;
d /4=BIR;
B=d /4IR;
Ответ: B=d /4IR=8кТл.
Вдоль длинного тонкостенного круглого цилиндра радиуса R=5,0см течет ток I=50A. Какое давление испытывают стенки цилиндра?
Решение:
P=F/S; S=2rH-боковая поверхность;
На цилиндр дейстует сила Ампера
F=BIL=BIH;
B= IL/4r теперь подставим все в формулу для давления
P= BIH/2rH= I /8 r .
Ответ: P= I /8 r .
2.277 Внутри длинного цилиндрического сосуда радиуса a параллельно его оси расположен проводящий стержень радиуса b с тонкой изоляцией. Расстояние между осями стержня и сосуда равно l. Сосуд заполнили электролитом и пустили вдоль оси ток I, возвращающийся обратно по стержню. Найти модуль и направление магнитной силы, действующей на единицу длины стержня.
Решение:
П
усть
h-
высота сосуда.
В
силу симметрии
(1)
Определение Ω2:
-
уравнение
окружности
Т. к. ρ не может быть меньше нуля, то
т. к. подынтегральная
функция нечетная
Из
(1)
По
3-му закону Ньютона сила стремится
прижать провод к стенке сосуда (на рис.
это сила
).
Ответ:
,
направление силы указано на рис. в
решении задачи (сила
).