Задача №2.149.

Имеется плоский воздушный конденсатор, S-площадь обкладки. Какую работу против электрических сил надо совершить чтобы увеличить расстояние между обкладками от до , если при этом поддерживать неизменным:

А) заряд конденсатора q;

Б) напряжение на конденсаторе U.

Решение:

Рассмотрим случай (а):

q=const; W= ; С= .

Следовательно,

;

Отсюда получим,

2.158 При каком сопротивлении R_x в цепочке (рис. 2.35) сопротивление между точками A и B не зависит от числа ячеек?

Р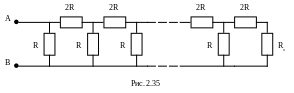 ешение:

Пусть n- число ячеек.

Рекурсивное задание:

1. n=1;

2)

По условию задачи

;

; ;

Т. к. , то

Ответ: .

№2.161. Однородная слабо проводящая среда с удельным сопротивлением ρ заполняет пространство между двумя коаксиальными идеально проводящими тонкими цилиндрами. Радиусы цилиндров a и b, причём a<b, длина каждого цилиндра ι. Пренебрегая краевыми эффектами, найти сопротивление среды между цилиндрами.

Решение :

Очевидно, что элементарное сопротивление длины dr и площади 2πrl :

Откуда, проинтегрировав от a до b, получим:

Ответ:

Задача № 2.164 (3.158)

Два металлических шарика одинакового радиуса а находятся в однородной слабо проводящей среде с удельным сопротивлением . Найти сопротивление среды между шариками при условии, что расстояние между ними значительно больше а.

Решение:

I=4Пa²j из закона Ома: j=E/, где E=q/4П₀а² подставим: I=q/₀; U=₊+_-=2q/4П₀а

Тогда R=U/I= /2Па.

Задача 2.168. Два проводника произвольной формы находятся в безграничной однородной слабо проводящей среде с удельным сопротивлением  и диэлектрической проницаемостью . Найти значение произведения RC для данной системы, где R  сопротивление среды между проводниками, С  взаимная емкость проводников при наличии среды.

Решение: R= , a

C= , отсюда

RC=

Ответ: RC=

2.176 Длинный проводник круглого сечения радиуса сделан из материала, удельное сопротивление которого зависит только от расстояния до оси проводника по закону , где - постоянная. Найти:

1. сопротивление единицы длинны такого проводника;

2. напряжённость электрического поля, при которой в проводнике будет протекать ток .

Решение: copyright 2001 Андрюха, 13РФ.

1. Пусть – сопротивление такого проводника длины . Разобьём проводник на вложенные цилиндры толщины 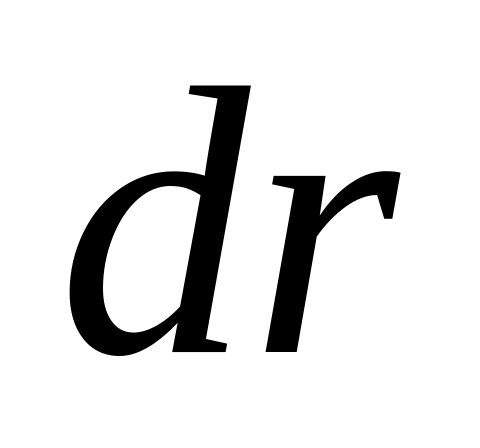. Проводник можно рассматривать как совокупность таких цилиндров, соединённых параллельно. Тогда имеем ; ; .

2. .

N-2.177.

Конденсатор С=400 пФ подключили через сопротивление R=650 Ом к источнику

Постоянного напряжения .Через сколько времени напряжение на конденсаторе

Станет U= ?

Решение :

I=dQ/dt; Q=Cφ; RI=ε-φ; dQ/dt+Q/RC=ε/R

d(Q-εC)/dt + (Q-εC)/RC=0 ;

Решая получаем :

Q= εC+Aexp(-t/τ);

(A – постоянная интегрирования , из условия T=0, Q=0; A=- εC );

Q= εC(1-exp(-t/τ)) ; По условию Q=Cφ=CU; ε=U ;

U=U - U exp(-t/τ)

exp(-t/τ)=( U - U)/ U =1- U/ U ; (τ=RC);

-t/RC=ln(1- U/ U ) t=-RCln(1- U/ U ) ;

Ответ : t=-RCln(1- U/ U ) .

2.178

Конденсатор, заполненный диэлектриком с проницаемостью ,1, теряет за время

мин половину сообщенного ему заряда. Считая, что утечка заряда происходит только через диэлектрическую прокладку, найти ее удельное сопротивление.

Решение:

 ;

;  ;  ;

; 

Ответ: .

2.179. Условие: Цепь состоит из источника  и последовательно подключенных к нему R и c. Внутреннее сопротивление источника мало. В момент времени t=0 ёмкость быстро уменьшили в раз. Найти ток в цепи как функцию от времени.

Решение: = R+ ;

q`R+(/c)q=/R; - линейное неоднородное дифференциальное уравнение.

q= +p , p=const, которую мы находим из начальных условий;

q₀=c/+p;

p=c ;

I=-p ;

I= *(/R) .

2.184

Резистор с сопротивлением R и нелинейное сопротивление, вольтамперная характеристика которого U=aI^1/2 , где a – постоянная, соединены последовательно и подключены к напряжению U₀ Найти ток в цепи.

Решение:

По закону Ома:

Ответ:

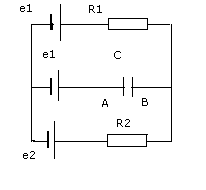
2.186. В схеме (рис 2.41) ξ₁=1,0 В, ξ₂=2,5 В, R₁=10 Ом, R₂=20 Ом. Внутренние сопротивления источников пренебрежимо малы. Найти разность потенциалов φ_a-φ_b, между обкладками конденсатора С.

Решение.

По правилам Киргофа:

(ξ₁-ξ₂)=I(R1+R₂);

I=(ξ₁-ξ₂)/(R₁+R₂);

Но с другой стороны для другого контура:

ξ₁+IR₁=ξ₁+(φ_A-φ_B);

φ_A-φ_B=(ξ₁-ξ₂)*R₁/(R₁+R₂);

Ответ: φ_A-φ_B=(ξ₁-ξ₂)*R₁/(R₁+R₂);

Задача №2.189.

Найти сопротивление и общую э.д.с. двух источников, соединенных параллельно, если э.д.с. каждого из них и , а также их сопротивления равны соответственно и ?

РЕШЕНИЕ:

Вначале найдем общее сопротивление полученной батареи. Так как наши источники соединены параллельно, получим:

;

Тогда для общего сопротивления запишем следующую формулу:

;

Для нахождения суммарной э.д.с. воспользуемся Законом Ома:

;

Сила тока определяется выражением:

;

В итоге получим:

.