
- •1. Экономико-математическая модель транспортной задачи.
- •2. Обща формулировка тз
- •3. Теорема (о ранге системы ограничений закрытой тз) и следствие из неё. Открытая тз.
- •4. Оценка свободной клетки, ее экономический смысл, критерий оптимальности базисного распределения поставок.
- •5. Теорема о потенциалах свободных клеток. Вычисление оценок свободных клеток методом потенциалов.
- •6. Понятие об игровых моделях.
- •7. Классификация игр.
- •8. Формальное представление игр.
- •9 .Принцип минимакса для антагонистических игр.
- •10.Фунд-ое нер-во для цен антагонистических игр.
- •11. Седловая точка. Теорема о седловой точке.
- •12. Понятие смешанной стратегии, чистой стратегии, активной стратегии.
- •14.Граф.Метод реш-ия игры 2х2 (формулы).
- •15.Доминирущие стратегии, заведомо невыгодные стратегии, упрощение игр.
- •16. Сведение игры mxn к двойственной задаче лп
- •17.Игры с природой: постановка задачи, матрица рисков.
- •18. Критерий принятия решений в условиях риска (Байеса 1 и 2). Лемма (показатели эффективности и неэффективности стратегии). Теорема об эквивалентности критериев Байеса.
- •19. Критерий принятия решений в условиях неопределенности: критерий Лапласа и Сэвиджа
- •20. Критерий принятия решений в условиях неопределенности: критерий Вальда и Гурвица
- •21.Общая постановка задачи динамического программирования (дп). Особенности задачи дп
- •22. Принцип оптимальности и уравнение Бэллмана
- •23. Задача о распределении средств между n предприятиями (основные уравнения)
- •25. Понятие маршрута, цепи, простой цепи, цикла для графа. Связные, несвязные графы. Дерево, лес.
- •26. Планарные и плоские графы. Изоморфные графы. Полные графы.
- •27. Эйлеровы графы. Критерий существования эйлерова цикла в графе. Полуэйлеров граф. Задача о Кенигсбергских мостах.
- •28. Гамильтонов граф. Достаточные признаки существования гамильтонова цикла (связь с полнотой цикла, теоремы Оре и Дирака). Полугамильтонов граф.
- •29.Орграфы, турниры. Предки и потомки вершин. Алгоритм Фалкерсона разбиения орграфа на слои.
- •30.Комбинаторная постановка задачи коммивояжера.
- •31. Постановка задачи коммивояжера в виде задачи целочисленного программирования. Условие наличия одного цикла.
- •32. Постановка задачи коммивояжера на языке теории графов.
- •33. Теорема о приведения матрицы расстояний в зк. Оценка маршрута снизу (нижняя граница).
- •34. Ветвление, оценки нулевых переходов, уточнение нижней границы маршрута.
- •35. Метод ближайшего соседа: эвристический алгоритм. Верхняя граница маршрута.
33. Теорема о приведения матрицы расстояний в зк. Оценка маршрута снизу (нижняя граница).
34. Ветвление, оценки нулевых переходов, уточнение нижней границы маршрута.
Метод ветвей и границ для решения задачи о коммивояжере – один из наиболее эффективных и быстрых методов решения задачи о коммивояжере, был разработан Литтлом, Мерти, Суини, Кэрелом в 1963 г. Представляет собой итеративную схему неявного (улучшенного) перебора, который состоит в отбрасывании заведомо неоптимальных решений и является одной из самых эффективных процедур в группе методов ветвей и границ.
Алгоритм метода.
Метод состоит из предварительного этапа и общего, который повторяется необходимое число раз.
Предварительный
этап.
Приведение матрицы затрат
![]() ,
вычисление нижней оценки стоимости
маршрута r.
,
вычисление нижней оценки стоимости
маршрута r.
Вычисление наименьшего элемента по каждой строке (константы приведения):
![]() ,
,
![]() .
(3.15)
.
(3.15)
Переход к новой матрице с элементами:
![]() .
(3.16)
.
(3.16)
Вычисление наименьшего элемента по каждому столбцу (константы приведения):
![]() ,
,
![]() .
(3.17)
.
(3.17)
Переход к новой матрице с элементами:
![]() .
(3.18)
.
(3.18)
Вычисление нижней оценки стоимости маршрута (сумма констант приведения):
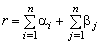 .
(3.19)
.
(3.19)
В
результате выполнения предварительного
этапа получаем матрицу
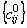 в
каждой строке и в каждом столбце которой
есть хотя бы один нулевой элемент.
в
каждой строке и в каждом столбце которой
есть хотя бы один нулевой элемент.
Общий этап.
1.
Вычисление штрафа “за неиспользование”
![]() для
каждого нулевого элемента приведенной
матрицы
.
для
каждого нулевого элемента приведенной
матрицы
.
Если
ребро (h,k) не включается в маршрут, то в
него входит некоторый элемент строки
h и столбца k. Следовательно, стоимость
«неиспользования» (h,k) во всяком случае,
не меньше суммы минимальных элементов
строки h и столбца k, исключая сам элемент
![]() .
Отсюда
.
Отсюда
 .
(3.20)
.
(3.20)
2.
Выбор нулевого элемента, которому
соответствует максимальный штраф. Если
таких элементов несколько, то выбирается
любой из них. Разбиение множества всех
допустимых маршрутов
![]() на
два подмножества: подмножество содержащее
ребро (h,k) –
на
два подмножества: подмножество содержащее
ребро (h,k) –
![]() ;
подмножество, не содержащее ребро (h,k)
–
;
подмножество, не содержащее ребро (h,k)
–
![]() .
.
Примечание: максимальный штраф означает, что исключение из решения переезда, соответствующего нулевому элементу, приведет к максимальному увеличению стоимости оптимального маршрута.
3. Вычисление оценок затрат по всем маршрутам, входящим в каждое подмножество.
3.1.
Обозначим за
![]() минимальную
оценку стоимости маршрутов, вошедших
в множество
,
т.е. не содержащих ребро (h,k). Для
оценка
затрат:
минимальную
оценку стоимости маршрутов, вошедших
в множество
,
т.е. не содержащих ребро (h,k). Для
оценка
затрат:
![]() .
(3.21)
.
(3.21)
3.2.
При вычислении оценки затрат для
учитывают,
что, если ребро (h,k) входит в маршрут, то
ребро (k,h) не может входить в маршрут,
поэтому принимаем:
![]() ;
если в маршрут включено ребро (h,k), то ни
одно другое ребро, начинающееся в пункте
h или заканчивающееся в пункте k не может
входить в маршрут, поэтому строка h и
столбец k вычеркиваются. Полученная
матрица приводится, т.е. выполняется
предварительный этап алгоритма. Пусть
сумма приводящих констант матрицы:
;
если в маршрут включено ребро (h,k), то ни
одно другое ребро, начинающееся в пункте
h или заканчивающееся в пункте k не может
входить в маршрут, поэтому строка h и
столбец k вычеркиваются. Полученная
матрица приводится, т.е. выполняется
предварительный этап алгоритма. Пусть
сумма приводящих констант матрицы:
![]() .
Тогда оценка затрат:
.
Тогда оценка затрат:
![]() .
(3.22)
.
(3.22)
4.
Из множеств
и
для
дальнейшего ветвления выбирается
множество, имеющее меньшую оценку. При
выборе
нужно
вернуться к шагу 1, используя на этом
шаге приведенную матрицу, полученную
на шаге 3.2. При выборе
нужно
вернуться к матрице
![]() ,
принять
,
принять
![]() и
привести полученную в результате
матрицу, после чего перейти к шагу 2,
используя на нем эту приведенную матрицу.
Если несколько множеств имеют равную
минимальную оценку, то дальнейшее
ветвление производится для всех множеств
с минимальной оценкой. Таким образом
метод ветвей и границ позволяет находить
все оптимальные решения.
и
привести полученную в результате
матрицу, после чего перейти к шагу 2,
используя на нем эту приведенную матрицу.
Если несколько множеств имеют равную
минимальную оценку, то дальнейшее
ветвление производится для всех множеств
с минимальной оценкой. Таким образом
метод ветвей и границ позволяет находить
все оптимальные решения.
Алгоритм
продолжается до тех пор, пока в подмножестве
маршрутов с наименьшей оценкой не
останется всего один маршрут. В расчетах
это соответствует ситуации, когда
исследуемая матрица имеет размерность
![]() .
.
