26. Планарные и плоские графы. Изоморфные графы. Полные графы.

Граф называется планарным, если он может быть изображен на плоскости таким образом, что его ребра будут пересекаться только в планарных вершинах

Существует правило изображение графов на поверхности: рёбра графа должны пересекаться только своими концами, то есть в точках, представляющих вершины графа. Граф, изображённый подобным образом называется плоским графом.

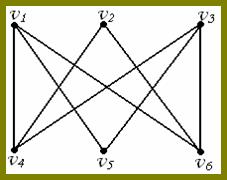
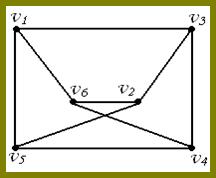
Графы G’ и G’’ называются изоморфными, если существует взаимно-однозначное соответствие (биекция) между их ребрами и вершинами, причем ребра соединяют соответствующие вершины

Изоморфизм графов означает, что можно так переобозначить вершины первого графа, что в новых обозначениях вершины и ребра будут совпадать со вторым графом

ПРИМЕР ИЗОМОРФНЫХ ГРАФОВ

Граф называется полным, если любая пара вершин соединена одним ребром

27. Эйлеровы графы. Критерий существования эйлерова цикла в графе. Полуэйлеров граф. Задача о Кенигсбергских мостах.

Эйлеров путь (эйлерова цепь) в графе — это путь, проходящий по всем рёбрам графа и притом только по одному разу. (ср. Гамильтонов путь)

Эйлеров цикл — это эйлеров путь, являющийся циклом.

Эйлеров граф — граф, содержащий эйлеров цикл.

Эйлеров цикл/путь существуют только в связных графах или в графах, которые после удаления всех одиночных вершин превратятся в связные.

В неориентированном графе

Кроме того, согласно теореме, доказанной Эйлером, эйлеров цикл существует тогда и только тогда, когда граф связный и в нём отсутствуют вершины нечётной степени.

Эйлеров путь в графе существует тогда и только тогда, когда граф связный и содержит не более чем две вершины нечётной степени. Ввиду леммы о рукопожатиях, число вершин с нечётной степенью должно быть четным. А значит Эйлеров путь существует только тогда, когда это число равно нулю или двум. Причём когда оно равно нулю, эйлеров путь вырождается в эйлеров цикл.

В ориентированном графе

Ориентированный граф содержит эйлеров цикл тогда и только тогда, когда он сильно-связан и для каждой вершины графа её полустепень захода равна её полустепени исхода, то есть в вершину входит столько же ребер, сколько из неё и выходит.

Полуэйлеров граф — граф, содержащий эйлеров путь (цепь).

Задача о Кенигсбергских мостах. Однажды великому математику Леонарду Эйлеру был задан вопрос: можно ли обойти все семь мостов, стоявших тогда в городе Кёнигсберге (современный Калининград, Россия), побывав на каждом по одному разу? Рассмотрев эту задачу, в 1736 году Эйлер доказал, что это невозможно, причем он рассмотрел более общую задачу: какие местности, разделенные рукавами рек и соединенные мостами, возможно обойти, побывав на каждом мосту ровно один раз, а какие невозможно.

28. Гамильтонов граф. Достаточные признаки существования гамильтонова цикла (связь с полнотой цикла, теоремы Оре и Дирака). Полугамильтонов граф.

Граф называется гамильтоновым, если для каждой вершины графа найдется маршрут начинающейся и заканчивающей в этой вершине и проходящий через все вершины только один раз. Такой маршрут называется гамильтоновым циклом.

Условия существования

Необходимое условие

Если неориентированный граф G содержит гамильтонов цикл, тогда в нём не существует ни одной вершины x(i) с локальной степенью p(x(i)) < 2. Доказательство следует из определения.

Условие Дирака (англ.) (1952)

Пусть p — число вершин в данном графе; если степень каждой вершины не меньше, чем  , то граф называется графом Дирака. Граф Дирака — гамильтонов.

Условие Оре (1960)

Пусть p — количество вершин в данном графе. Если для любой пары несмежных вершин x,y выполнено неравенство  , то граф называется графом Оре (словами: степени любых двух несмежных вершин не меньше общего числа вершин в графе). Граф Оре — гамильтонов.

Полугамильтонов граф — граф, который содержит простую цепь, проходящую через каждую его вершину. Всякий гамильтонов граф является полугамильтоновым