9 .Принцип минимакса для антагонистических игр.

B1 B2 …Bn min

A1 P11 P12…P1n α1

A2 P21 P22…P2n α2

. . . . .

Am Pm1 Pm2 ..Pmn αm

max β1 β2… βn

Игр А выб.стр. миним.затрат какую бы стр.не выбрал игр В.

α=maxαi=max(minpij)-макс.-нижняя цена,

β=minβj=min (maxpij)-миним.-верхняя цена.

10.Фунд-ое нер-во для цен антагонистических игр.

α< β

α β

Если α= β, то говорят, что игра имеет цену:

1) Ư(ню блять)=α=β

2) игра без седловой точки

3) она имеет решение в чистых стратегиях

если α < β

1) α<Ư<β

2)Игра без седловой точки

3) решение в смешанных стратегиях – чередование чистых стратегий случайным образом.

B1 B2 B3 min

A 1 10 11 8 8

A 2 14 16 9 9

7 9 6 6

max 14 16 9 α=9

β=9

Игра имеет цену

Ư(ню блять)=9

А*=А2

B*=B3

11. Седловая точка. Теорема о седловой точке.

Седловая точка-это значение, минимальное в своем столбце и максимальное в своей строке.

Теорема о седловой точке: Пара {x∗, u∗} удовлетворяет условию глобальной оптимальности тогда и только тогда, когда она является седловой точкой функции Лагранжа

12. Понятие смешанной стратегии, чистой стратегии, активной стратегии.

Смешанная стратегия является указанием вероятности каждой чистой стратегии. Это означает, что игрок выбирает одну из чистых стратегий, в соответствии с вероятностями заданными смешанной стратегией. Выбор осуществляется перед началом каждой игры и не меняется до её конца. Каждая чистая стратегия является частным случаем смешанной, когда вероятность данной чистой стратегии 1 и у всех других нулевая вероятность.

Чистая стратегия даёт полную определённость каким образом игрок продолжит игру. В частности, она определяет результат для каждого возможного выбора, который игроку может придётся сделать.

Активная стратегия-

13. Теорема об активных стратегиях: Если один из игроков придерживается своей оптимальной смешанной стратегии, то выигрыш остается неизменным и равным цене игры v, если второй игрок не выходит за пределы своих активных стратегий.

S_A=(p₁,p₂…p_m)

S_B=(q₁,q₂…q_n)

14.Граф.Метод реш-ия игры 2х2 (формулы).

Рассмотрим игру без седловой точки типа 2 x 2 с платежной матрицей

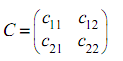
и найдем оптимальную стратегию игрока А.

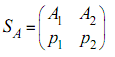
эта стратегия обеспечивает игроку A выигрыш, равный цене игры V, даже если игрок B не выходит за пределы своих полезных стратегий. В данной игре обе чистыетстратегии игрока B являются полезными, поскольку в противном случае игра имела бы решение в области чистых стратегий, т.е. была бы игрой с седловой точкой.

Отсюда вытекает, что неизвестные V, удовлетворяют следующей

системе из трех линейных уравнений

решение которой имеет вид

Аналогичным образом можно найти оптимальную стратегию

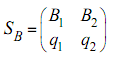
игрока B. В этом случае неизвестные V, удовлетворяют системе урав-

нений

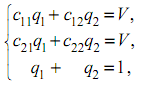
решение которой имеет вид

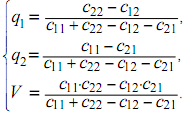
Применим теперь полученные формулы к карточной игре типа "веришь

- не веришь".

15.Доминирущие стратегии, заведомо невыгодные стратегии, упрощение игр.

Доминирующая стратегия. Простейшим примером стратегии является так называемая доминирующая стратегия. Такое положение возникает, когда один из игроков обладает лучшей стратегией независимо от того, какой стратегии следуют другие игроки.

Если у каждого из игроков имеется доминирующая стратегия, то исходом такой игры будет доминирующее равновесие.

Заведомо невыгодные стратегии.

Платежную матрицу нужно упростить до матрицы (2 × n) или (m × 2), для этого ищем заведомо невыгодные стратегии. Для игрока А, если все элементы одной стратегии почленно меньше или равны элементам какой-нибудь другой стратегии (так как игрок А максимизирует выигрыш), то такая стратегия заведомо невыгодна и ее нужно удалить. Для игрока В все элементы заведомо невыгодной стратегии больше или равны элементам другой стратегии (так как игрок В минимизирует проигрыш).

Упрощение игр.

Если платежная матрица игры не содержит седловой точки, то задача определения оптимальной смешанной стратегии тем сложнее, чем больше размерность матрицы. Поэтому для игр с платежными матрицами большой размерности отыскание решения можно упростить, если уменьшить их размерность путем вычерчивания дублирующих изведомо невыгодных стратегий, а также замены некоторых групп чистых стратегий смешанными.  Опр.: Если в матрице   игры все элементы строки(столбца) равны соответствующим элементам другой строки(столбца), то соответствующие строкам(столбцам) стратегии называются дублирующими.  Опр.: Если в матрице   игры все элементы некоторой строки определяют стратегию   игрока I не больше соответсвующих элементов другой строки, то стратегия  называется заведомо невыгодной.  Опр.: Если в матрице   игры все элементы некоторого столбца, определяющие стратегию   игрока II не меньше соответствующих элементов другого столбца, то стратегия  называется заведомо невыгодной.