
Методические указания по выполнению лабораторной работы
«Решение нелинейных уравнений»
Оглавление
Общие положения 1
1 этап. 1
2 этап. 3
Метод половинного деления (дихотомии) 3
Метод хорд 6
Метод Ньютона (касательных). 10
Общие положения
Решением или корнями уравнения Y(x)=0, называются такие значения аргумента х, при которых значение функции Y(x) становится равным нулю (равенство обращается в верное тождество). Только 2 класса уравнений – линейное ax + b = 0 и квадратное ax2 + bx + c = 0 – имеют в общем случае аналитическое решение в виде формул. Все остальные классы уравнений имеют аналитические решения только в некоторых частных случаях.
В данной лабораторной работе мы познакомимся с численными методами нахождения корней для любых классов уравнений. При этом определять значение корня мы будем с некоторой заданной точностью .
Вычисление корня нелинейного уравнения осуществляется в 2 этапа:
1 этап. Определение промежутков локализации [a, b]. Промежуток локализации [a, b] это такой промежуток обязательно есть корень функции, причем только один. Определение промежутков локализации выполняется с помощью построения таблицы значений и графика функции;
2 этап. Уточнение корней из выбранных промежутков локализации. На этом этапе применяются методы метод половинного деления (дихотомии) , касательных (Ньютона), хорд и другие.
1 Этап.
Промежуток [a, b], на котором следует искать корень функции должен удовлетворять 2 условиям:
- функция Y(x) должна быть непрерывна на этом промежутке [a, b]:
- значения функции Y(x) на концах промежутка в точках a и b должны иметь разные знаки Y(a) * Y(b) < 0
Рассмотрим уравнение x3 -5x + 3 = 0. функция Y(x) = x3 -5x + 3 является непрерывной при любом х, так что первое условие выполняется всегда. Для определения промежутков, где функция меняет знак, построим таблицу значений функции. См. рисунок 1.
X |
Y(x)=x3-5x +3 |
|
|
|
|
-3 |
-9 |
|
|
|
|
-2.5 |
-0.125 |
первый корень в
промежутке [-2.5, -2]
|
|||
-2 |
5 |
||||
-1.5 |
7.125 |
|
|
|
|
-1 |
7 |
|
|
|
|
-0.5 |
5.375 |
|
|
|
|
0 |
3 |
|
|
|
|
0.5 |
0.625 |
второй корень в
промежутке [0.5, 1]
третий корень в
промежутке [1, 1.5]
|
|||
1 |
-1 |
||||
1.5 |
-1.125 |
||||
2 |
1 |
||||
Рис. 1
Поскольку на промежутке от -2.5 до -2 функция Y(x) поменяла знак, (Y(-2.5)=-0.125, Y(-2.0)=5) и функция непрерывна, то где-то на этом промежутке она принимает значение 0, то есть на этом промежутке у функции Y(x) = x3 -5x + 3 есть корень. У кубической функции должно быть 3 корня, что и обнаруживается при дальнейшем анализе таблицы.
На рисунке 2 представлен график этой функции, иллюстрирующий промежутки локализации корней.
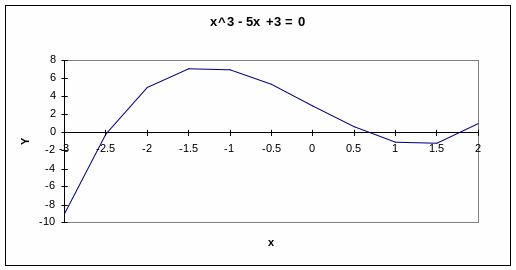
Рис. 2
Рассмотрим другой пример: tg(x) – x + 2 =0, левую часть уравнения обозначим Z(x)= tg(x) – x + 2. Как известно, tg(x) имеет разрывы в точках x= /2 n. Построим таблицу значений функции Z(x), как показано на рисунке 3.
x |
tg(x)-x+2 |
|
|
|
|
|
-2.5 |
5.247 |
На промежутке [
-2, -1.5] разрыв функции
|
||||
-2 |
6.185 |
|||||
-1.5 |
-10.601 |
Корень на промежутке
[ -1.5 до -1.0]
|
|
|
|
|
-1 |
1.443 |
|
|
|
|
|
-0.5 |
1.954 |
|
|
|
|
|
0 |
2.000 |
|
|
|
|
|
0.5 |
2.046 |
|
|
|
|
|
1 |
2.557 |
|
|
|
|
|
1.5 |
14.601 |
На промежутке [
1.5, 2.0] разрыв функции
|
||||
2 |
-2.185 |
|||||
2.5 |
-1.247 |
|
|
|
|
|
3 |
-1.143 |
|
|
|
|
|
Рис. 3.
Первое изменение знака функции Z(x) мы видим на промежутке [-2.0, -1.5], однако в точке x= -/2 = -1.5759 имеется разрыв функции, нарушено условие непрерывности, поэтому на промежутке [-2.0, -1.5] корня нет. На промежутке [-1.5, -1.0] опять изменился знак функции, при чем на этом промежутке функция Z(x) непрерывна, поэтому промежуток [-1.5, -1.0] является промежутком локализации и содержит корень функции. Дальнейший анализ таблицы значений показывает, что на промежутке [1.5, 2.0] снова происходит смена знака функции, но в точке x= /2 = 1.5759 имеется разрыв функции, следовательно корня на этом промежутке нет.
Рисунок 4 показывает график функции Z(x)= tg(x) – x + 2. На рисунке видно, что на промежутках [-2.0, -1.5] и [1.5, 2.0] не может быть корней функции Z(x).
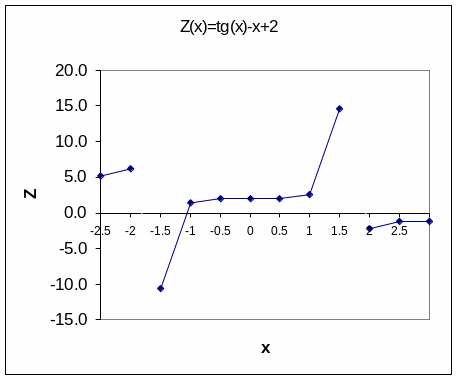
Рис. 4.
