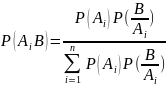Правила вычисления вероятностей

Условная вероятность – вероятность одного события при условии, что другое событие уже произошло.

Суммой двух случайных событий А и В наз события, состоящие в появлении события А, или события В, или обоих этих событий (лог «или»).

Суммой нескольких случайных событий наз событие, которое состоит в появлении хотя бы одного из этих событий.

Произведением двух случайных событий А и В наз событие, состоящее в совместном двух этих появлении (лог «и»).

Произведением нескольких случайных событий наз событие, состоящее в повялении всех этих событий одновременно.

Теорема сложения вероятностей несовместных событий

Теорема: Вероятность суммы конечного числа несовместных событий равна сумме вероятностей этих событий

P

Док-во

Докажем эту теорему для случая суммы двух несовм соб 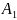и . Пусть соб благоприятствуют элементарных исходов, а событию - исходов. Так как соб и по условию несовместны, то соб + благоприятствуют + элементарных исходов из общего числа n-исходов =>

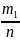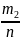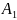P( + )= = + =P( , где P( – вероябтность события ; - вероятн соб .

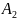Теорема сложения вероятностей совместных событий

Теорема: Два соб наз совместными, если появление одного из них не исключает появления другого в одном и том же опыте. Р(А+В)=Р(А)+Р(В)-Р(АВ)

Док-во

Событие А+В наступит, если наступат одно из трех несовместных событий А , В, АВ. По теореме сложения вероятностей несовм соб имеем Р(А+В)=Р(А)+Р(В)-Р(АВ) (1)

Событие А произойдет, если наступит одно из двух несовм соб: А , АВ. Вновь применяя теоремы сложения вероятн несовм соб, получим Р(А)=Р(А )+Р(АВ) (2)

Откуда Р(А )=Р(А)-Р(АВ) (3) Р(В)=Р( В)+Р(АВ) (4) Ан-но для второго события. Откуда: Р( В)=Р(В)-Р(АВ) (5)

Подставив 3 и 4 в 5, получим: Р(А+В)=Р(А)+Р(В)-Р(АВ)

Теорема умножения вероятностей для двух произвольных событий

Теорема: Вероятность произведения двух соб равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое имело место. Р(АВ)=Р(А)Р( )=Р(В)Р( )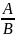

Док-во

Предположим, что из n всевозможных элементарн исходов событию А благоприятствуют m исходов, из которых k исходов благоприятствуют соб В. Тогда вероятность соб А будет Р(А)= , условная вероятность соб В относительно соб А будет Р( )=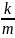 . Произведению событий А и В благоприятствуют только те исходы, которые благоприятствуют и соб А и событию В одновременно, то есть k исходов. Поэтому вероятность произведения соб А и В равна: Р(АВ)= .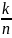

Умножим числитель и знаменатель дроби на m. Получим: Р(АВ)= =Р(А)Р( )

Ан-но док и формула: Р(АВ)=Р(В)Р( )

Теорема умножения вероятностей двух независимых событий

Теорема: Теорема произведения конечного числа событий равна произведению их условий вероятностей относительно произведения предшествующих событий.

Так как события независимые, то верно равенство: (В)=Р(В) => Р(АВ)=Р(А)Р(В)

Формула полной вероятности

Предположим, что событие В может осуществляться только с одним из несовместных событий .

P(B)=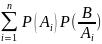

Формула Байеса

Пусть событие В происходит одновременно с одним из n несовместных событий . Требуется найти вероятность события , если известно, что событие В произошло. На основании теоремы о вероятности произведения двух событий можно написать:

P( B)=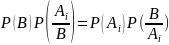 =>