
- •Ядерный магнитный резонанс.
- •1.Ядерный магнетизм.
- •2.Ларморовская прецессия спина.
- •3.Ядерный парамагнетизм.
- •4.Ядерный ферромагнетизм.
- •5.История развития методов ямр в медицине .
- •6.Ямр первого рода.
- •7.Ямр второго рода.
- •8.Уравнение Блоха для установления статистического равновесия.
- •9.Импульсные последовательности в ямр-томографах.
- •10.Устройство томографа.
6.Ямр первого рода.
Рассмотрим следующую установку:

1 – постоянные магниты (создают однородное магнитное поле B0).
2 – дуанты (создают низкочастотное магнитное поле B1).
 (6.1)
(6.1)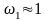 Гц,
Гц,
 сонаправлен с
.
сонаправлен с
.
3 – атомные ядра (вещество,в которые они входят).
4 – катушка.
5 – амперметр.
6 – источник
высокочастотных напряжений В’:
 (6.2)
(6.2)
При включенном
напряжении в катушке возникает
высокочастотный ток, а значит и
высокочастотное магнитное поле В’.
Частота меняется: где
- ларморовская частота прецессии
атомных ядер во внешнем магнитом поле
В0.
где
- ларморовская частота прецессии
атомных ядер во внешнем магнитом поле
В0.
Когда
возникает резонанс. Кванты высокочастотного
магнитного поля
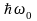 начинают
поглощаться ядром, а значит, в ядре
происходят переходы на более высокие
положения:
начинают
поглощаться ядром, а значит, в ядре
происходят переходы на более высокие
положения:

Наблюдаем следующие явления: увеличение эффективного сопротивления, уменьшение тока и добротности. По уменьшению тока мы судим о наличии резонанса.
Если бы отсутствовали
дуанты, то
 ,
(частота должна быть подобрана очень
точно).
,
(частота должна быть подобрана очень
точно).

Г (ширина уровня) мала, поэтому тяжело попасть в резонанс. Дуанты же создают переменное магнитное поле.
 (6.3)
(6.3)
амплитуда достаточно большая и за период можем 2 раза попасть в резонанс.
Такой ядерный резонанс позволят очень точно мерить поля в тканях и органах.
1-ый тип ЯМР – энергетический тип (осуществляется через энергетические потери).
Магнитный резонанс приводит к повороту спина ядра, а через управление спином ядра и проводится ядерная магнитная томография.
7.Ямр второго рода.
Для описания прецессий магнито-дипольного момента ядер выгодно перейти во вращающуюся систему координат. Уравнение изменения любого вектора во вращающейся системе координат:
 (7.1)
(7.1)
где w – вектор угловой скорости , с которой вращается система координат, A’ - вектор во вращающейся системе координат, A - вектор в лабораторной системе координат.
В качестве вектора
A возьмем вектор
магнито-дипольного момента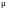 .
.
 (7.2)
(7.2)
где - гиромагнитное отношение,
- гиромагнитное отношение,
 - изменение магнито-дипольного момента
во внешнем однородном поле B0.
- изменение магнито-дипольного момента
во внешнем однородном поле B0.
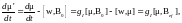 (7.3)
(7.3)
где
 (7.4) – эффективное магнитное поле.
(7.4) – эффективное магнитное поле.
Частота ларморовской
прецессии ,
значит
,
значит (7.5)
(7.5)
Если выберем w=w0
то (на магнито-дипольный момент не действует
никаких пар сил, он не изменяется
(на магнито-дипольный момент не действует
никаких пар сил, он не изменяется
 = const). Переход во вращательную
систему координат позволяет
скомпенсировать внешнее магнитное
поле
= const). Переход во вращательную
систему координат позволяет
скомпенсировать внешнее магнитное
поле
 .
.
 (7.6)
(7.6)
Где В0 - постоянное однородное магнитное поле, В’ - высокочастотное поле.
 (7.7)
(7.7)
где
 и
и
 соответственно
амплитуда и частота изменения поля.
соответственно
амплитуда и частота изменения поля.
 содержит
2 компоненты (вращение с частотой
и
содержит
2 компоненты (вращение с частотой
и ):
):
 (7.8)
(7.8)
Если система координат
вращается с угловой скоростью
,
то в этой системе вращение, связанное
с членом пропадает (происходит остановка
вращения для этого члена). Второй член
будет вращаться с удвоенной частотой.
пропадает (происходит остановка
вращения для этого члена). Второй член
будет вращаться с удвоенной частотой.
Явление резонансного
поглощения кванта магнитного поля
происходит в том случае, если
 ,
тогда первый член осуществляет переход
под влиянием возмущения, зависящего
от времени.
,
тогда первый член осуществляет переход
под влиянием возмущения, зависящего
от времени.
Резонансный член Вторая экспонента в резонанс не попадает.

Резонанс происходит , если переход осуществляется вверх. У второго члена этого перехода нет, поэтому пренебрегаем им, сохраняя член .
Наложим на ядерную
систему два поля
и
 и перейдем во вращательную систему
координат с частотой
,
тогда в этой системе высокочастотное
поле останавливается и внешнее
магнитное поле становится постоянным
полем
.
и перейдем во вращательную систему
координат с частотой
,
тогда в этой системе высокочастотное
поле останавливается и внешнее
магнитное поле становится постоянным
полем
.
Если сделаем частоту (условие резонанса), то вращение полностью компенсирует поле .
На магнито-дипольный момент будет действовать постоянное магнитное поле .
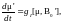 (7.9)
(7.9)
начнется прецессия вокруг поля .
Направим поле
по
оси х, тогда магнито-дипольный момент
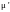 будет прецессировать вокруг поля
.
будет прецессировать вокруг поля
.

При этом прецессия
будет иметь постоянное направление
вдоль х.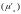
Если в мы имели намагниченность ядер вдоль B0 (по оси z), то, включив высокочастотное магнитное поле и перейдя во вращательную систему координат получили отличную от нуля компоненту µ, направленную вдоль х. ( разворачивается на 90°).
Если перейти обратно в лабораторную систему координат, то будет вращаться с угловой скоростью вокруг поля (оси z). испытывает двойное вращение , иксовая компонента сохраняется.
Решим задачу в общем
случае:
 направлено
вдоль х (перпендикулярно
),
тогда
направлено
вдоль х (перпендикулярно
),
тогда
 (7.10) где
(7.10) где
 –
вектор во вращательной системе
координат.
–
вектор во вращательной системе
координат.
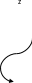
 (7.11)
(7.11)
где a
– эффективная частота,
 (7.12)
где
(7.12)
где (7.13)
(7.13)
Пусть в момент времени t=0 магнито-дипольный момент был ориентирован по оси z.

Нужно найти угол
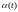 –
угол между В и осью z.
–
угол между В и осью z.
 (7.14).
(7.14).
Рассмотрим скалярное
произведение, у
 выделим две компоненты, первая из
которых направлена вдоль ОС, а вторая
компонента – на АС, тогда:
выделим две компоненты, первая из
которых направлена вдоль ОС, а вторая
компонента – на АС, тогда:
 ,
,
 ,
,
Рассмотрим несколько
предельных случаев: в общем случае
будем рассматривать
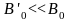 (то есть амплитуда высокочастотного
поля гораздо меньше амплитуды постоянного
магнитного поля), а значит, для
ларморовских частот имеем:
(то есть амплитуда высокочастотного
поля гораздо меньше амплитуды постоянного
магнитного поля), а значит, для
ларморовских частот имеем:
 .Первый
случай, случай далекий от резонанса,
то есть
.Первый
случай, случай далекий от резонанса,
то есть
 ,
тогда
,
тогда
 ,
мы пренебрегли
,
мы пренебрегли
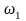 их
начального условия, значит
их
начального условия, значит
 ,
тогда
,
тогда
 ,
,
 ,
то есть угол
,
то есть угол
 мал, поэтому
мал, поэтому
 ,
мы учли что
,
мы учли что
 ,
значит максимальное значение
,
значит максимальное значение
 .
.
Окончательно получили,
что
 ,
а при малых
,
а при малых
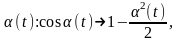
 .
.
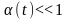 ,
значит
,
значит
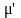 при прецессии будет слабо уходить от
оси z.
при прецессии будет слабо уходить от
оси z.
Второй случай,


Когда
 можем
набирать любые углы и значит
можем
набирать любые углы и значит
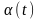 принимает
любые значения, и можем повернуть
принимает
любые значения, и можем повернуть
 под
любым углом к z. А, если
под
любым углом к z. А, если
 ,
то направление
на ось x, если же угол
,
то направление
на ось x, если же угол
 -
инверсия.
-
инверсия.
И третий случай,
случай чистого резонанса:

 прецессия
относительно 0x, вращение
с ларморовской частотой.
прецессия
относительно 0x, вращение
с ларморовской частотой.
В случае резонанса, если намагничиваем ядерную систему в направлении поля , когда направлено параллельно оси 0z, при включении высокочастотного поля, направленного вдоль 0x, можем повернуть вектор на любой угол.
Рассмотрим какие
времена нужны, чтобы получать разные
направления
.
Направленный вдоль 0x
 с
направлением прецессии вдоль y
выберем таким, когда
с
направлением прецессии вдоль y
выберем таким, когда
 где
где
 -
время за которое угол α станет равным
π/2. Это случай
-
время за которое угол α станет равным
π/2. Это случай
 .
.
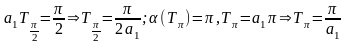 -
инверсия. При переходе в лабораторную
систему координат, которая вращается
со скоростью
-
инверсия. При переходе в лабораторную
систему координат, которая вращается
со скоростью
 относительно
вращательной системы координат,
относительно
вращательной системы координат,

 направленно
вдоль x. Выключим поле и
перейдем в лабораторную систему
координат со скоростью
направленно
вдоль x. Выключим поле и
перейдем в лабораторную систему
координат со скоростью
 ,
параллельно 0z, а, значит,
прецессия идет в плоскости xy.
Направление поляризации было вдоль 0z,
,
параллельно 0z, а, значит,
прецессия идет в плоскости xy.
Направление поляризации было вдоль 0z,
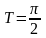 .
При переходе получили абсолютный
поворот (
.
При переходе получили абсолютный
поворот ( вращается
в плоскости xy). Если
вращается
в плоскости xy). Если
 направлен вдоль 0z во
вращательной системе координат, значит,
при переходе в лабораторную систему
координат ничего не меняется и вектор
остался инверсионным – абсолютная
инверсия.
направлен вдоль 0z во
вращательной системе координат, значит,
при переходе в лабораторную систему
координат ничего не меняется и вектор
остался инверсионным – абсолютная
инверсия.
Неэнергетический принцип – принцип резонанса по вращению.
