Ядерный магнитный резонанс.

1.Ядерный магнетизм.

Атомные ядра со спином не равным нулю могут иметь магнитный дипольный момент.

, (1.1)

Где ядерный магнетон, - масса протона, спин, полное гиромагнитное отношение, состоящее из – орбитального гиромагнитного отношения и – спинового гиромагнитного отношения, где , .

Для основных состояний четно-четных ядер спин равен нулю. Для нечетных ядер спин равен спину последнего неспаренного нуклона. Для нечетно-нечетных ядер спин равен сумме нечетных p и нечетных n.

Ядро водорода – протон, он обладает большими значениями . В атомных ядрах гиромагнитное отношение достигает десятков.

Системы атомных ядер со спином не равным 0 обладают ядерным магнетизмом.

Существуют следующие виды магнетиков: диамагнетики, парамагнетики, ферромагнетики, сверхпроводники, антиферромагнетики. У систем атомных ядер магнетизм парамагнитного типа. В системах атомных ядер при понижении температуры может возникнуть ферромагнетизм.

Пусть внешнее магнитное поле 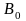действует на систему ядер. Во внешнем магнитном поле с ядром происходят следующие эффекты: 1) появляется дополнительная потенциальная энергия (потенциальная функция).

,(1.2)

А также рассмотрим силы, действующие на ядро. 2) Обычная сила.

_(1.3)

_{Уравнение Ньютона для обычной силы (уравнение движения под действием силы): в гамильтониановой форме : . Где -обобщенные координаты, - обобщенный импульс.( для поля, неоднородного по α).}

3)Ядро может вращаться, т. е. обобщенными координатами будут являться углы.

– угол поворота. По отношению к обобщенной силой является пара сил .

, (1.4)

Где µ - магнитный дипольный момент (1.1).

Обобщенный импульс для угла – момент количества движения. Уравнение Ньютона для вращения: полный момент количества движения ядра – спин: (1.5).

Изменение спина ядра во внешнем магнитном поле (из (1.1) и (1.5)): (1.6), получили ларморовскую прецессию спина (вращение спина).

2.Ларморовская прецессия спина.

1. Решаем уравнение классически.

, .

Векторное произведение: где

Получаем систему: Z-овая проекция - константа.

,(2.2)

(2.1.2)*i + (2.1.1) и учтем (2.2) (2.3) – ларморовская частота, где - ядерный магнетон.

Напишем действительную и мнимую часть величины А:

Вращение происходит в плоскости перпендикулярной плоскости z. X и y меняются по законам вращения. Вращение с ларморовской частотой. Вектор спина вращается вокруг поля .

2. Решаем уравнение квантово - механически.

(2.4), спин принимает дискретные значения.

Собственные значения

значит число различных проекций спина на z :

Если до включения магнитного поля все состояния ядра со спином I были вырождены (энергия не зависела от ), то при включении происходит вырождение по

Спектр ядра в этом случае (для ):

Без магнитного поля уровни имели одинаковую энергию, затем произошло расщепление по уровням, при этом расстояние между уровнями:

(2.5)

Где - ларморовская частота (2.3).

Если Т=0 (абсолютный ноль), то при этой температуре все ядра в основном состоянии (I_z=I). (Когда направление спина ядра направлено по полю В₀). При этом происходит полная поляризация (сильнейший уровень поляризации).

При Т≠0 наблюдается ядерный парамагнетизм.