1.1.2. Электропроводность собственного полупроводника

Количественная оценка электропроводности в полупроводниках и, в частности, в собственном полупроводнике, основана на статистике Ферми-Дирака (Э.Ферми – итал., 1901–1954; П.Дирак – англ., 1902–1984), устанавливающей закон распределения носителей заряда по уровням в ВЗ и ЗП при данной температуре. Согласно этой статистике, функция Ферми-Дирака характеризует вероятность заполнения энергетических уровней частицами (электронами), которая фактически эквивалентна среднему числу этих частиц в уровнях , т. е.

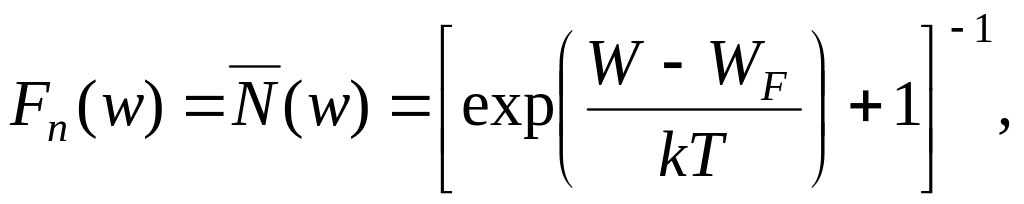(2)

где k=1,38·10^-23Дж/К = 8,62·10^-5эВ/К – постоянная Больцмана (Л. Больцман – австр., 1844-1906); Т – температура, К; – энергия уровня Ферми; кТ – величина, характеризующая среднее значение энергии теплового движения электронов, которая при комнатной температуре (условно при 300К)

Это распределение в случае собственного полупроводника, которое для наглядности совмещено со схемой энергетических зон, показано на рис. 3,а.

Из рисунка видно, что при Т=0К функция , т. е. все уровни ВЗ полностью заполнены с вероятностью, равной единице, в то время как вероятность заполнения любого уровня ЗП (прямые 1), что соответствует об отсутствии проводимости кристалла [8].

При комнатной температуре (Т≈300К) за счет термогенерации носителей и их переброса из ВЗ в ЗП функция , а и появляется электропроводность (кривая 2). При дальнейшем повышении температуры ( ) вероятность любого разрешенного уровня стремится к величине (прямая 3).

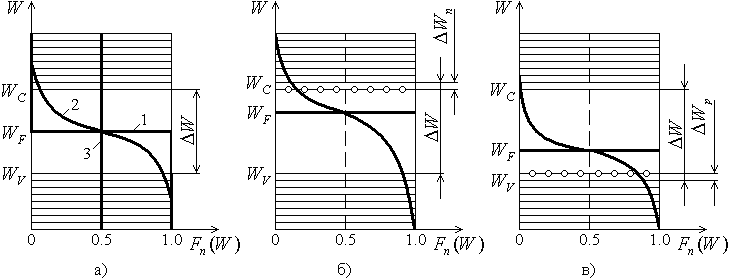
Рис. 3. Зонная модель и функция Ферми-Дирака в полупроводниках а – собственном; б – примесном n-типа; в – примесном p-типа

Из (2) следует, что при функция Ферми-Дирака

(3)

т.е. становится очевидным определение уровня Ферми как энергетического уровня, для которого при любой температуре вероятность занятия (или незанятия) его электронами составляет 0,5, т. е. 50 %.

Положив в (2) , получим

(4)

где – ширина запрещенной зоны.

Для количественной оценки электропроводности необходимо знать полное число электронов в зоне проводимости, т. е. их концентрацию. Теоретический анализ собственной электропроводности полупроводников показывает, что при термическом возбуждении в кристалле при постоянной температуре устанавливается статическое равновесие между числом переходов электронов в ЗП (генерацией пар электрон-дырка) и числом обратных переходов электронов в ВЗ (рекомбинацией носителей) [9]. При этом установившаяся равновесная концентрация электронов n в ЗП и дырок p в ВЗ характеризуется известным уравнением действующих масс:

(5)

где – концентрации электронов и дырок в чистом (собственном) полупроводнике; и – соответственно эффективные плотности энергетических уровней в зонах проводимости и валентной, которые примерно равны в германии 5·10¹⁹см = 5·10²⁵м^-3; в кремнии 2·10¹⁹см^-3 = 2·10²⁵м^-3.

Из соотношения (5) получим выражение для собственной концентрации носителей

(6)

Подставляя значение и в (6), получим уравнения, определяющие собственные концентрации носителей заряда в германии и кремнии:

(7)

(8)

При комнатной температуре .

Таким образом, собственная концентрация носителей, от которой зависит электропроводность, определяется шириной ЗЗ и температурой.

При отсутствии внешнего электрического поля никаких токов в полупроводнике нет, и он остается электронейтральным, так как все направления теплового движения носителей зарядов равновероятны [8]. Напротив, под действием приложенного электрического поля хаотическое тепловое движение электронов и дырок приобретает упорядоченное взаимнопротивоположное направление вдоль поля. Возникает общий, так называемый, дрейфовый ток (ток проводимости), плотность j которого равна сумме электронной и дырочной составляющих

(9)

Перемещение подвижных носителей под действием приложенного внешнего напряжения сопровождается многочисленными столкновениями их с атомами кристаллической решетки. В промежутках между столкновениями электроны приобретают энергию от электрического поля, а при столкновении ее теряют. В результате электрон движется с некоторой средней скоростью , пропорциональной напряженности электрического поля Е:

(10)

где - подвижность электрона (аналогично - подвижность дырки), равная средней скорости, приобретаемой носителем заряда в электрическом поле с единичной напряженностью Е [8,10]. Для германия , , а для кремния , .

Аналогично для дырок:

(11)

В соответствии с [2,8,9] плотность тока j равна общему заряду q электронов в единице объема с концентрацией n, проходящему через единичное сечение проводника. Поэтому с учетом (10) и (11) имеем для электронной и дырочной составляющих плотности:

(12)

(13)

Кроме того, в соответствии с законом Ома плотность тока определяется

(14)

где и – соответственно удельные электропроводность и сопротивление.

Из выражений (9), (12), (13) и (14) следует, что общая плотность дрейфового тока и удельная электропроводность определяются как

(15)

(16)

Для собственного полупроводника и тогда

(17)

(18)

Подставляя в (18) из уравнения (6), получаем окончательное выражение для собственной электропроводности полупроводника

(19)

где .

Соответственно для удельного сопротивления имеем:

(20)

где .

Таким образом, электропроводность собственного полупроводника зависит от концентрации носителей зарядов, их подвижности и температуры. Чем выше температура, тем удельная электропроводность выше, причем, эта зависимость носит экспоненциальный характер [11].