1

1).Химические превращения. Основные стехиометрические законы химии

Стехиометрия — раздел химии, в котором рассматриваются массовые или объемные соотношения между реагирующими веществами. Исключительное значение для развития химии имело установление основных стехиометрических законов.

1. Закон сохранения массы веществ (М. В. Ломоносов, 1748-1756 гг., А. Лавуазье, 1777 г.).

Масса веществ, вступивших в реакцию, равна массе веществ, получившихся в результате реакции.

Закон сохранения массы веществ может быть объяснен с точки зрения атомно-молекулярного учения так: при химических реакциях атомы не исчезают и не могут возникать из ничего; общее число атомов остается постоянным до и после реакции. Например, при взаимодействии двухатомных молекул водорода и хлора должно образоваться столько молекул НС1, чтобы число атомов водорода и хлора оставалось равным двум, т.е. две молекулы:

И поскольку атомы имеют постоянную массу, не меняется и масса веществ до и после реакции.

Закон сохранения массы веществ М. В. Ломоносов связывал с законом сохранения энергии (количества движения). Он рассматривал эти законы в единстве как всеобщий закон природы.

Таким образом, законы сохранения массы веществ и сохранения энергии — это две стороны единого закона природы — закона вечности материи и ее движения.

Взаимосвязь массы и энергии (она рассматривается в физике) выражают уравнением Эйнштейна:

E=mc2,

где E — энергия; m — масса; c — скорость света в вакууме.

Закон сохранения массы веществ дает материальную основу для составления уравнений химических реакций. Опираясь на него, можно проводить расчеты по химическим уравнениям.

2. Закон постоянства состава вещества (Ж. Л. Пруст, 1808 г.).

Каждое чистое вещество независимо от способа его получения всегда имеет постоянный качественный и количественный состав.

Атомно-молекулярное учение позволяет объяснить закон постоянства состава. Например, воду можно получить по любой из следующих реакций:

2Н2+О2=2Н2О

Са(ОН)2=СаО+Н2О

CuSO4•5Н2О=CuSO4+5Н2О

Химически чистая вода содержит 11,19% водорода и 88,81% кислорода, независимо от способа ее получения, то есть на один атом кислорода приходится два атома водорода. Иной состав свидетельствует либо о наличии примесей, либо о том, что это другое вещество (например, Н2О2).

Ж. Пруст писал: «От одного полюса Земли до другого соединения имеют одинаковый состав и одинаковые свойства. Никакой разницы нет между оксидом железа из Южного полушария и Северного. Малахит из Сибири имеет тот же состав, как и малахит из Испании».

В этой формулировке закона, как и в приведенном выше, подчеркивается постоянство состава соединения независимо от способа получения и места нахождения.

3.Закон кратных отношений (Д. Дальтон):

Если два элемента образуют между собой несколько молекулярных соединений, то масса одного элемента, приходящаяся на одну и ту же массу другого, относятся между собой как небольшие целые числа.

При взаимодействии азота с кислородом образуются пять оксидов. На 1 грамм азота в образующихся молекулах приходится 0,57, 1,14, 1,71, 2,28, 2,85 грамм кислорода, что соответствует отношением 2:1, 1:1, 2:3, 1:2, 2:5 в этих оксидах; их составы N2O, NO, N2O3, NO2, N2O5.

4.Закон простых объемных отношений (Ж. Гей-Люссак):

При равных условиях объемы вступающих в реакцию газов относятся друг к другу и к объемам образующихся газообразных продуктов, как небольшие целые числа.

Так, в реакции образования аммиака из простых веществ отношение объемов водорода, азота и аммиака составляет 3 : 1 : 2.

5.Закон Авогадро: В равных объемах любых газов, взятых при одинаковых условиях, содержится одинаковое число молекул.

Из закона Авогадро вытекают два следствия:

-Одинаковое количество молекул любых газов при одинаковых условиях занимают одинаковый объем.

-Относительная плотность одного газа по другому равна отношению их молярных масс.

Число Авогадро – число частиц в моле любого вещества; NA = 6,02?1023 моль–1.

Молярный объем – объем моля любого газа при нормальных условиях(температура 273 К, давление 101,3 кПа); равен 22,4 л?моль–1.

Молярная масса (M) – масса одного моля вещества, численно совпадающая с относительными массами атомов, ионов, молекул, радикалов и других частиц, выраженных в г?моль–1.

2

Современная модель атома является развитием планетарной модели. Согласно этой модели, ядро атома состоит из положительно заряженных протонов и не имеющих заряда нейтронов и окружено отрицательно заряженными электронами. Однако представления квантовой механики не позволяют считать, что электроны движутся вокруг ядра по сколько-нибудь определённым траекториям (неопределённость координаты электрона в атоме может быть сравнима с размерами самого атома).  Химические свойства атомов определяются конфигурацией электронной оболочки и описываются квантовой механикой. Положение атома в таблице Менделеева определяется электрическим зарядом его ядра (то есть количеством протонов), в то время как количество нейтронов принципиально не влияет на химические свойства; при этом нейтронов в ядре, как правило, больше, чем протонов (см.: атомное ядро). Если атом находится в нейтральном состоянии, то количество электронов в нём равно количеству протонов. Основная масса атома сосредоточена в ядре, а массовая доля электронов в общей массе атома незначительна (несколько сотых процента массы ядра).  Массу атома принято измерять в атомных единицах массы, равных 1⁄12 от массы атома стабильного изотопа углерода 12C.

Французский ученый Луи де Бройль (1892—1987), осознавая существующую в природе симметрию и развивая представления о двойственной корпускулярно-волновой природе света, выдвинул в 1923 г. гипотезу об универсальности корпускулярно-волнового дуализма. Де Бройль утверждал, что не только фотоны, но и электроны и любые другие частицы материи наряду с корпускулярными обладают также волновыми свойствами.

Итак, согласно де Бройлю, с каждым микрообъектом связываются, с одной сторо­ны, корпускулярные характеристики — энергия Е и импульс p, а с другой —волновые характеристики — частота  и длина волны . Количественные соотношения, связыва­ющие корпускулярные и волновые свойства частиц, такие же, как для фотонов:

                                             (213.1)

Смелость гипотезы де Бройля заключалась именно в том, что соотношение (213.1) постулировалось не только для фотонов, но и для других микрочастиц, в частности для таких, которые обладают массой покоя. Таким образом, любой частице, обладающей импульсом, сопоставляют волновой процесс с длиной волны, определяемой по формуле де Бройля:

                                                    (213.2)

Это соотношение справедливо для любой частицы с импульсом р.

Вскоре гипотеза де Бройля была подтверждена экспериментально. В 1927 г. американские физики К. Дэвиссон (1881—1958) и Л. Джермер (1896—1971) обнаружили, что пучок электронов, рассеивающийся от естественной дифракционной решетки — кри­сталла никеля, — дает отчетливую дифракционную картину. Дифракционные максимумы соответствовали формуле Вульфа — Брэггов (182.1), а брэгговская длина волны оказалась в точности равной длине волны, вычисленной по формуле (213.2). В даль­нейшем формула де Бройля была подтверждена опытами П. С. Тартаковского и Г. Томсона, наблюдавших дифракционную картину при прохождении пучка быстрых электронов (энергия  50 кэВ) через металлическую фольгу (толщиной 1 мкм).

Так как дифракционная картина исследовалась для потока электронов, то необходимо было доказать, что волновые свойства присущи не только потоку большой совокупности электронов, но и каждому электрону в отдельности. Это удалось экспериментально подтвердить в 1948 г. российскому физику В. А. Фабриканту (р. 1907). Он показал, что даже в случае столь слабого электронного пучка, когда каждый электрон проходит через прибор независимо от других (промежуток времени между двумя электронами в 10⁴ раз больше времени прохождения электроном прибора), возникающая при длительной экспозиции дифракционная картина не отличается от дифракционных картин, получаемых при короткой экспозиции для потоков электронов, в десятки миллионов раз более интенсивных. Следовательно, волновые свойства частиц не являются свойством их коллектива, а присущи каждой частице в отдельности.

Впоследствии дифракционные явления обнаружили также для нейтронов, протонов, атомных и молекулярных пучков. Это окончательно послужило доказательством нали­чия волновых свойств микрочастиц и позволило описывать движение микрочастиц в виде волнового процесса, характеризующегося определенной длиной волны, рас­считываемой по формуле де Бройля (213.2). Открытие волновых свойств микрочастиц привело к появлению и развитию новых методов исследования структуры веществ, таких, как электронография и нейтронография, а также к возникновению новой отрасли науки — электронной оптики.

Экспериментальное доказательство наличия волновых свойств микрочастиц приве­ло к выводу о том, что перед нами универсальное явление, общее свойство материи. Но тогда волновые свойства должны быть присущи и макроскопическим телам. Почему же они не обнаружены экспериментально? Например, частице массой 1 г, движущейся со скоростью 1 м/с, соответствует волна де Бройля с  = 6,6210^–31 м. Такая длина волны лежит за пределами доступной наблюдению области (периодических структур с периодом d10^–31 м не существует). Поэтому считается, что макроскопические тела проявляют только одну сторону своих свойств — корпускулярную — и не проявляют волновую.

Представление о двойственной корпускулярно-волновой природе частиц вещества углубляется еще тем, что на частицы вещества переносится связь между полной энергией частицы  и частотой  волн де Бройля:

                                                                      (213.3)

Это свидетельствует о том, что соотношение между энергией и частотой в формуле (213.3) имеет характер универсального соотношения, справедливого как для фотонов, так и для любых других микрочастиц. Справедливость же соотношения (213.3) вытекает из согласия с опытом тех теоретических результатов, которые получены с его помощью в квантовой механике, атомной и ядерной физике.

Подтвержденная экспериментально гипотеза да Бройля о корпускулярно-волновом дуализме свойств вещества коренным образом изменила представления о свойствах микрообъектов. Всем микрообъектам присущи и корпускулярные, и волновые свойства; в то же время любую из микрочастиц нельзя считать ни частицей, ни волной в классическом понимании. Современная трактовка корпускулярно-волнового дуализма может быть выражена словами академика В. А. Фока (1898—1974): «Можно сказать, что для атомного объекта существует потенциальная возможность проявлять себя, в зависимости от внешних условий, либо как волна, либо как частица, либо промежуточным образом. Именно в этой потенциальной возможности различных проявлений свойств, присущих микрообъекту, и состоит дуализм волна—частица. Всякое иное, более буквальное, понимание этого дуализма в вида какой-нибудь модели неправильно».

Формула Планка — выражение для спектральной плотности мощности излучения абсолютно чёрного тела, которое было получено Максом Планком. Для плотности энергии излучения u(ω,T):

Уравнение Шредингера

Волновая функция

    Волновая функция (или вектор состояния) – комплексная функция, описывающая состояние квантовомеханической системы. Её знание позволяет получить максимально полные сведения о системе, принципиально достижимые в микромире. Так с её помощью можно рассчитать все измеряемые физические характеристики системы, вероятность пребывания её в определенном месте пространства и эволюцию во времени. Волновая функция может быть найдена в результате решения волнового уравнения Шредингера.      Волновая функция ψ(x, y, z, t) ≡ ψ(x,t) точечной бесструктурной частицы является комплексной функцией координат этой частицы и времени. Простейшим примером такой функции является волновая функция свободной частицы с импульсом   и полной энергией Е (плоская волна)

.

    Волновая функция системы А частиц содержит координаты всех частиц: ψ( ₁, ₂,..., _A,t).     Квадрат модуля волновой функции отдельной частицы |ψ( ,t)|² = ψ*( ,t)ψ( ,t) дает вероятность обнаружить частицу в момент времени t в точке пространства, описываемой координатами  , а именно, |ψ( ,t)|²dv ≡|ψ(x, y, z, t)|²dxdydz это вероятность найти частицу в области пространства объемом dv = dxdydz вокруг точки x, y, z. Аналогично, вероятность найти в момент времени t систему А частиц с координатами  ₁, ₂,..., _A в элементе объема многомерного пространства дается величиной |ψ( ₁, ₂,..., _A,t)|²dv₁dv₂...dv_A.     Волновая функция полностью определяет все физические характеристики квантовой системы. Так среднее наблюдаемое значение физической величины F у системы дается выражением

,

где   - оператор этой величины и интегрирование проводится по всей области многомерного пространства.     В качестве независимых переменных волновой функции вместо координат частиц x, y, z могут быть выбраны их импульсы p_x, p_y, p_z или другие наборы физических величин. Этот выбор зависит от представления (координатного, импульсного или другого).     Волновая функция ψ( ,t) частицы не учитывает ее внутренних характеристик и степеней свободы, т. е. описывает ее движение как целого бесструктурного (точечного) объекта по некой траектории (орбите) в пространстве. Этими внутренними характеристиками частицы могут быть её спин, спиральность, изоспин (для сильновзаимодействующих частиц), цвет (для кварков и глюонов) и некоторые другие. Внутренние характеристики частицы задаются специальной волновой функцией её внутреннего состояния φ. При этом полная волновая функция частицы Ψ может быть представлена в виде произведения функции орбитального движения ψ и внутренней функции φ:

Ψ = φψ,

поскольку обычно внутренние характеристики частицы и её степени свободы, описывающие орбитальное движение, не зависят друг от друга.      В качестве примера ограничимся случаем, когда единственной внутренней характеристикой, учитываемой функцией  , является спин частицы, причем этот спин равен 1/2. Частица с таким спином может пребывать в одном из двух состояний - с проекцией спина на ось z, равной +1/2 (спин вверх), и с проекцией спина на ось z, равной -1/2 (спин вниз). Эту двойственность описывают спиновой функцией   взятой в виде двухкомпонентного спинора:

Тогда волновая функция Ψ^+1/2 = χ^+1/2ψ будет описывать движение частицы со спином 1/2, направленным вверх, по траектории, определяемой функцией ψ , а волновая функция Ψ^-1/2 = χ^-1/2ψ будет описывать движение по той же траектории этой же частицы, но со спином, направленным вниз.     В заключении отметим, что в квантовой механике возможны такие состояния, которые нельзя описать с помощью волновой функции. Такие состояния называют смешанными и их описывают в рамках более сложного подхода, использующего понятие матрицы плотности. Состояния квантовой системы, описываемые волновой функцией, называют чистыми.

Электронные облака - орбитали

Е динственный электрон атома водорода образует вокруг ядра сферическую орбиталь - шарообразное электронное облако, вроде неплотно намотанного клубка пушистой шерсти или ватного шарика.

Сферическую атомную орбиталь ученые договорились называть s-орбиталью. Она самая устойчивая и располагается довольно близко к ядру.

Чем больше энергия электрона в атоме, тем быстрее он вращается, тем сильнее вытягивается область его пребывания и наконец превращается в гантелеобразную p-орбиталь:

Э лектронное облако такой формы может занимать в атоме три положения вдоль осей координат пространства x, y и z. Это легко объяснимо: ведь все электроны заряжены отрицательно, поэтому электронные облака взаимно отталкиваются и стремятся разместиться как можно дальше друг от друга. 

Все вместе три электронных облака, которые называют p_x-, p_y- или p_z-орбиталями, образуют симметричную геометрическую фигуру, в центре которой находится атомное ядро. Она похожа на шестиконечный помпончик или на тройной бант - кому как нравится.

Итак, p-орбиталей может быть три. Энергия их, конечно, одинакова, а расположение в пространстве - разное.

К роме s- и p-орбиталей, существуют электронные орбитали еще более сложной формы; их обозначают буквами d и f. Попадающие сюда электроны приобретают еще больший запас энергии, двигаются по сложным путям, и в итоге получаются сложные и красивые объемные геометрические фигуры.

Все d-орбитали (а их может быть уже пять) одинаковы по энергии, но по-разному расположены в пространстве. Да и по форме, напоминающей перевязанную лентами подушечку, одинаковы только четыре.  А пятая - вроде гантели, продетой в бублик.

3

Правило Гунда определяет порядок заполнения орбиталей определённого подслоя и формулируется следующим образом: суммарное спиновое число электронов данного подслоя должно быть максимальным.

Это означает, что в каждой из орбиталей подслоя заполняется сначала один электрон, а только после исчерпания незаполненных орбиталей на эту орбиталь добавлется второй электрон. При этом на одной орбитали находятся два электрона с полуцелыми спинами противоположного знака, которые спариваются (образуют двухэлектронное облако) и, в результате, суммарный спин орбитали становится равным нулю.

Другая формулировка: Ниже по энергии лежит тот атомный терм, для которого выполняются два условия. 1. Мультиплетность максимальна 2. При совпадении мультиплетностей суммарный орбитальный момент L максимален.

При́нцип Па́ули (принцип запрета) — один из фундаментальных принципов квантовой механики, согласно которому два тождественных фермиона не могут одновременно находиться в одном квантовом состоянии.

В атоме каждый электрон располагается так, чтобы его энергия была минимальной (что отвечает наибольшей связи его с ядром).

Энергия электрона в основном определяется главным квантовым числом n и побочным квантовым числом l, поэтому сначала заполняются те подуровни, для которых сумма значений квантовых чисел n и l является наименьшей. Например, энергия электрона на подуровне 4s меньше, чем на подуровне 3d, так как в первом случае n + 1 = 4 + 0 = 4, а во втором n + l = 3 + 2 =5; на подуровне 5s (n + l = 5 + 0 = 5) энергия меньше, чем на 4d (n + l = 4 + 2 = 6); на 5р (n + l = 5 + 1 = 6) энергия меньше, чем на 4f (n + l = 4 + 3 = 7) и т.д.

Правило Клечковского (также Правило n+l; также используется название правило Маделунга) — эмпирическое правило, описывающее энергетическое распределение орбиталей в многоэлектронных атомах.

Второе правило Клечковского, согласно которому при одинаковых значениях суммы (n+l) орбитали заполняются в порядке возрастания главного квантового числа n.

орбитальная энергия последовательно повышается по мере увеличения суммы , причём при одном и том же значении этой суммы относительно меньшей энергией обладает атомная орбиталь с меньшим значением главного квантового числа . Например, при орбитальные энергии подчиняются последовательности , так как здесь для -орбитали главное квантовое число наименьшее , для -орбитали ; наибольшее , -орбиталь занимает промежуточное положение .

Или же:

При заполнении орбитальных оболочек атома более предпочтительны (более энергетически выгодны), и, значит, заполняются раньше те состояния, для которых сумма главного квантового числа и побочного (орбитального) квантового числа , т.е. , имеет меньшее значение.

Электронную структуру атома можно схематически представить электронно-точечным символом, в котором электроны внешней оболочки ( или внешнего октета) указывают точками, а ядро вместе с внутренними электронами обозначают химическим символом данного элемента. Электронно-точечный символ лития ( Li -) показывает только внешний электрон, который называют валентным электроном. [4]

Электронную структуру атома можно схематически записать в виде электронно-точечных символов, в которых электроны внешней оболочки ( или внешнего октета) представляются точками, а ядро и внутренние электроны обозначаются химическим символом данного элемента. Электронно-точечный символ лития Li показывает только внешний электрон, называемый валентным. [5]

Вся электронная структура атома: общее число электронов в атоме, число электронных оболочек, число электронов в каждой электронной оболочке и число электронов в самой наружной электронной оболочке, оказывающее наибольшее влияние на химические свойства элемента, - вся эта структура в конечном счете определяется величиной положительного заряда ядра атома. Величина эта, как мы знаем, выражается порядковым номером элемента. Таким образом, величина заряда ядра является тем основным свойством элемента, от которого зависят другие его свойства. Следовательно, не масса атома ( его атомный вес) определяет свойства элемента, как считали Д. И. Менделеев и современные ему ученые, а величина положительного заряда его ядра. 

Порядок заполнения электронных оболочек (орбиталей с одинаковым значением главного квантового числа n) определяется правилом Клечковского, порядок заполнения электронами орбиталей в пределах одного подуровня (орбиталей с одинаковыми значениями главного квантового числа n и орбитального квантового числа l) определяется Правилом Хунда.

4

Квантовые числа — энергетические параметры, определяющие состояние электрона и тип атомной орбитали, на которой он находится.

1. Главное квaнтовое число n определяет общую энергию электрона и степень его удаления от ядра (номер энергетического уровня); оно принимает любые целочисленные значения, начиная с 1 (n = 1, 2, 3, . . .)

2. Орбитальное (побочное или азимутальное) квантовое число l определяет форму атомной орбитали. Оно может принимать целочисленные значения от 0 до n-1 (l = 0, 1, 2, 3,..., n-1). Каждому значению l соответствует орбиталь особой формы. Орбитали с l = 0 называются s-орбиталями, l = 1 – р-орбиталями (3 типа, отличающихся магнитным квантовым числом m), l = 2 – d-орбиталями (5 типов), l = 3 – f-орбиталями (7 типов).

3. Магнитное квантовое число m определяет ориентацию орбитали в пространстве относительно внешнего магнитного или электрического поля. Его значения изменяются от +l до -l, включая 0. Например, при l = 1 число m принимает 3 значения: +1, 0, -1, поэтому существуют 3 типа  р-АО:  р_x,  р_y,  р_z.

4. Спиновое квантовое число s может принимать лишь два возможных значения +1/2 и -1/2. Они соответствуют двум возможным и противоположным друг другу направлениям собственного магнитного момента электрона, называемого спином (от англ. веретено). Для обозначения электронов с различными спинами используются символы: 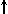и .

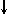Волновая функция (или вектор состояния) – комплексная функция, описывающая состояние квантовомеханической системы. Её знание позволяет получить максимально полные сведения о системе, принципиально достижимые в микромире. Так с её помощью можно рассчитать все измеряемые физические характеристики системы, вероятность пребывания её в определенном месте пространства и эволюцию во времени. Волновая функция может быть найдена в результате решения волнового уравнения Шредингера.      Волновая функция ψ(x, y, z, t) ≡ ψ(x,t) точечной бесструктурной частицы является комплексной функцией координат этой частицы и времени. Простейшим примером такой функции является волновая функция свободной частицы с импульсом   и полной энергией Е (плоская волна)

.

    Волновая функция системы А частиц содержит координаты всех частиц: ψ( ₁, ₂,..., _A,t).     Квадрат модуля волновой функции отдельной частицы |ψ( ,t)|² = ψ*( ,t)ψ( ,t) дает вероятность обнаружить частицу в момент времени t в точке пространства, описываемой координатами  , а именно, |ψ( ,t)|²dv ≡|ψ(x, y, z, t)|²dxdydz это вероятность найти частицу в области пространства объемом dv = dxdydz вокруг точки x, y, z. Аналогично, вероятность найти в момент времени t систему А частиц с координатами  ₁, ₂,..., _A в элементе объема многомерного пространства дается величиной |ψ( ₁, ₂,..., _A,t)|²dv₁dv₂...dv_A.     Волновая функция полностью определяет все физические характеристики квантовой системы. Так среднее наблюдаемое значение физической величины F у системы дается выражением

,

где   - оператор этой величины и интегрирование проводится по всей области многомерного пространства.     В качестве независимых переменных волновой функции вместо координат частиц x, y, z могут быть выбраны их импульсы p_x, p_y, p_z или другие наборы физических величин. Этот выбор зависит от представления (координатного, импульсного или другого).     Волновая функция ψ( ,t) частицы не учитывает ее внутренних характеристик и степеней свободы, т. е. описывает ее движение как целого бесструктурного (точечного) объекта по некой траектории (орбите) в пространстве. Этими внутренними характеристиками частицы могут быть её спин, спиральность, изоспин (для сильновзаимодействующих частиц), цвет (для кварков и глюонов) и некоторые другие. Внутренние характеристики частицы задаются специальной волновой функцией её внутреннего состояния φ. При этом полная волновая функция частицы Ψ может быть представлена в виде произведения функции орбитального движения ψ и внутренней функции φ:

Ψ = φψ,

поскольку обычно внутренние характеристики частицы и её степени свободы, описывающие орбитальное движение, не зависят друг от друга.      В качестве примера ограничимся случаем, когда единственной внутренней характеристикой, учитываемой функцией  , является спин частицы, причем этот спин равен 1/2. Частица с таким спином может пребывать в одном из двух состояний - с проекцией спина на ось z, равной +1/2 (спин вверх), и с проекцией спина на ось z, равной -1/2 (спин вниз). Эту двойственность описывают спиновой функцией   взятой в виде двухкомпонентного спинора:

Тогда волновая функция Ψ^+1/2 = χ^+1/2ψ будет описывать движение частицы со спином 1/2, направленным вверх, по траектории, определяемой функцией ψ , а волновая функция Ψ^-1/2 = χ^-1/2ψ будет описывать движение по той же траектории этой же частицы, но со спином, направленным вниз.     В заключении отметим, что в квантовой механике возможны такие состояния, которые нельзя описать с помощью волновой функции. Такие состояния называют смешанными и их описывают в рамках более сложного подхода, использующего понятие матрицы плотности. Состояния квантовой системы, описываемые волновой функцией, называют чистыми.