11. Полная механическая энергия системы. Закон сохранения механической энергии

Механическая энергия системы тел равна сумме их кинетических энергий и потенциальной энергии взаимодействия этих тел друг с другом и с внешними телами:

Е = Е_к + Е_п.

Приращение механической энергии системы определяется работой всех неконсервативных сил (внешних и внутренних):

.

Закон сохранения механической энергии: механическая энергия системы тел, на которые действуют только консервативные силы, остается постоянной.

Полной механической энергией системы тел называется сумма кинетической и потенциальной энергий:

E = E_к + E_п.

Какие причины могут изменить полную механическую энергию?

Р ассмотрим систему тел, в которой действуют следующие силы:

	fпот.с. - внутренняя потенциальная сила;
	fнепот.с. - внутренняя непотенциальная сила;
	Fвнеш.с. - внешняя сила.

12. Вращательное движение твердого тела. Момент инерции материальной точки и твердого тела относительно неподвижной оси. Кинетическая энергия вращающегося тела. Теорема Штейнера

И з основного закона динамики вращательного движения следует: если результирующий момент сил равен нулю, соответственно dL/dt=0, то означает суммарный момент импульса остаётся постоянным. Таким образом, если на систему не действуют ни ускорение, ни тормозящие моменты сил, то величина и направление момента импульса остаются постоянными.

J₁₁= J₂₂, если J₁ >J₂ ₂ >₁

L₁=L₂

§5.6 Вычисление момента инерции.

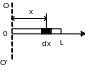Теорема Штейнера: Момент инерции тонкого стержня

dJ=dmx²

=m/ L – линейная плотность

dm=dx

d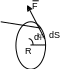 J= x²dx

Моменты инерции тел:

1) Материальная точка J=mR²

2) Обруч J=mR²

3) Диск (цилиндр) J=1/2mR²

4) Шар J=2/5mR²

5) Тонкий стержень J=1/12mL²

6) Полый цилиндр J=1/2(R₁²+R₂²)

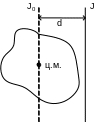
Если известен момент инерции относительно оси, проходящей через центр инерции J₀ , то момент инерции J относительно другой оси, параллельной первой, можно вычислить по формуле J=J₀ + md²

.7 Работа и кинетическая энергия при вращательном движении.

Вращение тела осуществляется тангенсальной составляющей силой, действующей на тело. Эта же сила совершает работу, величина которой на dS определяется соотношением:

dA=FdS

учитывая dS=dR, получаем dA=F_Rd

dA=Md

(при М-const), то результирующая работа определяется соотношением:

P=dA/dt=M

Кинетическая энергия вращательного тела равна сумме кинетических энергий его частиц:

Если тело участвует одновременно в поступательном и вращательном движении, то скорость его точки будет складываться из скорости центра масс и линейной скорости:

_i = _C +_i (_C – поступательная скорость центра, _I – линейная скорость вращения)

13. Работа, совершаемая при вращении твердого тела. Момент силы, относительно точки и оси вращения. Основное уравнение динамики вращательного движения твердого тела.

Момент силы от-но непод т-ки вращения- векторная величина= векторному произведению радиус-вектора в т-ке приложения силы на верток силы. М=r×F. Момент силы от-но непод оси вращения- скалярная величина = проекции на эту ось момента силы, определенного относительно произвольной т-ки этой оси. М_z=Mcosφ. М_z не зависит от выбора т.О на оси. Рассмотрим неподвиж тв тело,которое может вращаться вокруг неподвиж оси z,проходящей ч\з центр инерции тв тела. В некоторый момент времени на ТВ тело начинает действовать постоянная сила F,приложенная к т.В на расстоянии r от оси вращения