
- •1 Механическое движение. Элементы кинематики материальной точки: радиус-вектор, перемещение, скорость.
- •2. Ускорение точки. Нормальное и тангенциальное ускорение. Проекции ускорения на координатной оси.
- •3. Кинематика вращательного движения. Угловая скорость и ускорение.
- •Задачи динамики для свободной и несвободной мате риальной точки.
- •5. Инерциальные системы отсчета. Принцип относительности Галилея. Преобразование Галилея.
- •Формула преобразования скоростей
- •6.Силы внутренние и внешние. Замкнутая система отсчета. Закон сохранения импульса.
- •[Править]Центры масс однородных фигур
- •[Править]в механике
- •[Править]Центр масс в релятивистской механике
- •[Править]Центр масс системы материальных точек
- •8. Работа. Работа переменной силы. Мощность
- •Энергия. Кинетическая энергия материальной точки и тела, движущегося поступательно. Связь между изменением кинетической энергии и работой, действующих на тело сил.
- •10 Понятие силового поля. Силы консервативные и неконсервативные. Потенциальная энергия и ее связь с силой, действующей на материальную точку.
- •11. Полная механическая энергия системы. Закон сохранения механической энергии
- •§5.6 Вычисление момента инерции.
- •13. Работа, совершаемая при вращении твердого тела. Момент силы, относительно точки и оси вращения. Основное уравнение динамики вращательного движения твердого тела.
- •Основное уравнение динамики вращательного движения.
- •14. Момент импульса материальной точки и твердого тела относительно неподвижной оси вращения. Закон сохранения момента импульса
- •15. Предмет молекулярной физики и термодинамики. Термодинамические параметры системы. Идеальный газ. Уравнение состояния идеального газа.
- •16. Основное уравнение молекулярно-кинетической теории идеального газа для давления. Следствие из основного уравнения молекулярно-кинетической теории.
- •17. Скорости газовых молекул. Закон Максвелла для распределения молекул идеального газа по скоростям. Наиболее вероятная ,средняя квадратичная и средняя арифметическая скорости молекул.
- •18. Барометрическая формула. Распределение молекул в поле силы тяжести. Распределение Больцмана
- •19. Внутренняя энергия системы. Работа газа при изменениях его объема. Количество теплоты. Первое начало термодинамики.
- •20. Число степеней свободной молекулы. Закон равномерного распределения энергии по степеням свободы молекул. Внутренняя энергия идеально газа.
- •21. Теплоемкость. Зависимость теплоемкости идеального газа от вида процесса. Классическая теория теплоемкости идеального газа и ее ограниченность
- •22. Применение первого начала термодинамики к изопроцессам в газах.
- •23. Применение первого начала термодинамики к адиабатическому процессу. Политропический процесс.
- •[Править]Первое начало термодинамики
- •[Править]Уравнение Пуассона
- •[Править]Показатель адиабаты
- •24. Поверхностный слой жидкости. Поверхностное натяжение. Коэффициент поверхностного натяжения и его зависимость от температуры и примесей пав
- •25. Давление под изогнутой поверхностью жидкости. Формула Лапласа. Капиллярные явления
- •Формула Лапласа
- •26. Явления смачивания. Краевой угол. Свойства тонких пленок.
[Править]Центры масс однородных фигур
У отрезка — середина.
У многоугольников (как сплошных плоских фигур, так и каркасов):
У параллелограмма — пересечение диагоналей.
У треугольника — точка пересечения медиан (центроид).
У правильного многоугольника — центр поворотной симметрии.
[Править]в механике
Понятие центра масс широко используется в физике.
Движение твёрдого тела можно рассматривать как суперпозицию движения центра масс и вращательного движения тела вокруг его центра масс. Центр масс при этом движется так же, как двигалось бы тело с такой же массой, но бесконечно малыми размерами (материальная точка). Последнее означает, в частности, что для описания этого движения применимы все законы Ньютона. Во многих случаях можно вообще не учитывать размеры и форму тела и рассматривать только движение его центра масс.
Часто бывает удобно рассматривать движение замкнутой системы в системе отсчёта, связанной с центром масс. Такая система отсчёта называется системой центра масс (Ц-система), илисистемой центра инерции. В ней полный импульс замкнутой системы всегда остаётся равным нулю, что позволяет упростить уравнения её движения.
[Править]Центр масс в релятивистской механике
В случае высоких скоростей (порядка скорости света) (например, в физике элементарных частиц) для описания динамики системы применяется аппарат СТО. В релятивистской механике (СТО) понятия центра масс и системы центра масс также являются важнейшими понятиями, однако, определение понятия меняется:
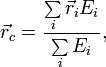
где
— радиус-вектор центра масс,
— радиус-вектор i-й частицы системы,
![]() — энергия i-й
частицы (E=Епок+Ek)
— энергия i-й
частицы (E=Епок+Ek)
Во избежание ошибок следует понимать, что в СТО центр масс характеризуется не распределением массы, а распределением энергии. В курсе теоретической физики Ландау и Лившица предпочтение отдается термину «центр инерции». В западной литературе по элементарным частицам применяется термин «центр масс» (center-of-mass). Оба термина эквивалентны.
[Править]Центр масс системы материальных точек
В системе материальных точек координаты центра масс могут быть определены по формулам:
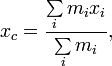
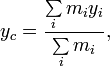
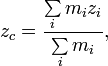
где ![]() -
суммарная масса системы;
-
суммарная масса системы; ![]() ,
, ![]() и
и ![]() —
координаты i-й
материальной точки;
—
масса i-й
материальной точки.
—
координаты i-й
материальной точки;
—
масса i-й
материальной точки.
8. Работа. Работа переменной силы. Мощность
Работа – это физическая величина, характеризующая процесс превращения одной формы движения в другую. В механике принято говорить, что работа совершается силой.
Элементарной
работой силы
называется величина, равная скалярному
произведению силы на элементарное
перемещение :
:
 ,
,
где
 –
элементарный путь точки приложения
силы за время dt,
– угол между векторами
и
.
–
элементарный путь точки приложения
силы за время dt,
– угол между векторами
и
.
Если на систему действуют несколько сил, то результирующая работа равна алгебраической сумме работ, совершаемых каждой силой в отдельности. Работа силы на конечном участке траектории или за конечный промежуток времени может быть вычислена следующим образом:
 .
.
Если
=
const, то А=
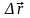 .
.
При вращательном движении работа определяется проекцией момента сил на направление угловой скорости:
 ,
,
если М = const, то А = М.
Быстроту совершения работы характеризует мощность. Мощностью называется скалярная величина, равная работе, совершаемой в единицу времени:
 – средняя
мощность;
– средняя
мощность; – мгновенная мощность.
– мгновенная мощность.
При вращательном движении мощность определяется следующим образом:
 .
.
Мощность — физическая величина, равная отношению работы, выполняемой за некоторый промежуток времени, к этому промежутку времени.
-
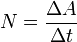 —
средняя
мощность
—
средняя
мощность
-
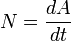 —
мгновенная
мощность
—
мгновенная
мощность
Так как работа является мерой изменения энергии, мощность можно определить также как скорость изменения энергии системы.
