10.Дисперсионный анализ

Дисперсионный анализ (ДА) широко применяется для изучения источников рассеивания СВ. В его основе лежит метод разложения общего рассеивания на компоненты, которые обусловлены факторами и случайной ошибкой наблюдения. Такое свойство ДА впервые было обнаружено Фишером в 1920 году.

Методы ДА позволяют отделить компоненты рассеивания, связанные с ошибкой наблюдения, от компонент, связанных с действующими факторами.

Пример. Однофакторный ДА (модель связана с источником рассеивания для одного фактора).

Пусть изучается рассеивание СВ Y, выборочное значение которой можно классифицировать по группам. Результаты сводятся в следующую таблицу:

Уровни факторов	1	2	…	j	...	k
1			…		…		_
2			…		…		_
...	…	…	…	…	…	…	_
i			…		…		_
...	…	…	…	…	…	…	_
			…		…		_
сумма			…		…
среднее			…		…

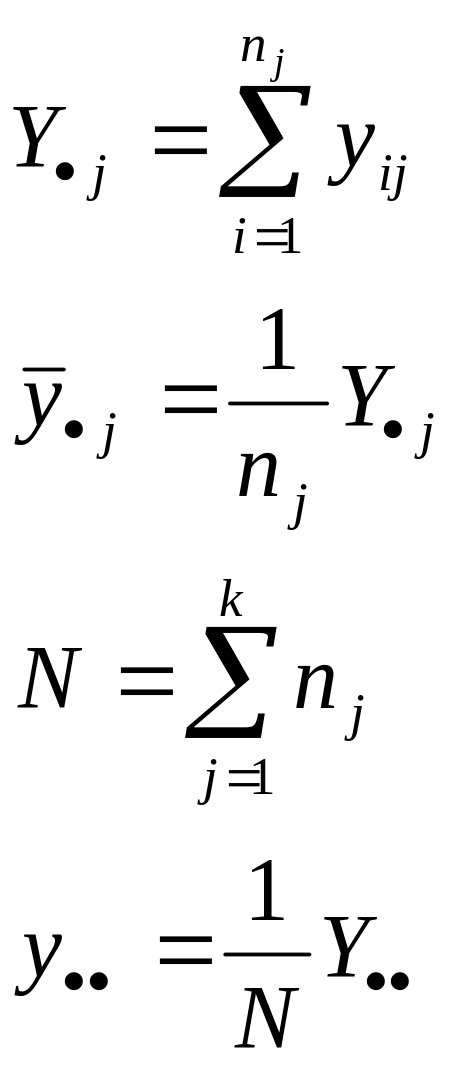
Рассмотрим следующие формулы:

где левая часть – уклонение наблюдаемого от среднего по таблице, первая скобка справа - уклонение среднего по уровню от среднего по таблице, вторая скобка справа – уклонение среднего наблюдаемого от среднего по уровню.

В результате основное тождество ДА показывает, что сумма квадратов уклонений наблюдаемого от среднего по таблице можно разделить на две составляющих:

1. одна связана с рассеиванием среднего по уровням от среднего по таблице;

2. вторая связана с рассеиванием частных средних.

SSобщ = SSур + SSост

SS – сумма квадратов отклонений;

S – оценка дисперсий.

Основному тождеству ДА соответствует основное тождество степеней свободы:

N-1 = (K-1) + (N-K)

Если разделить соответствующую SSобщ на (N-1), получим выражение для оценки дисперсии:

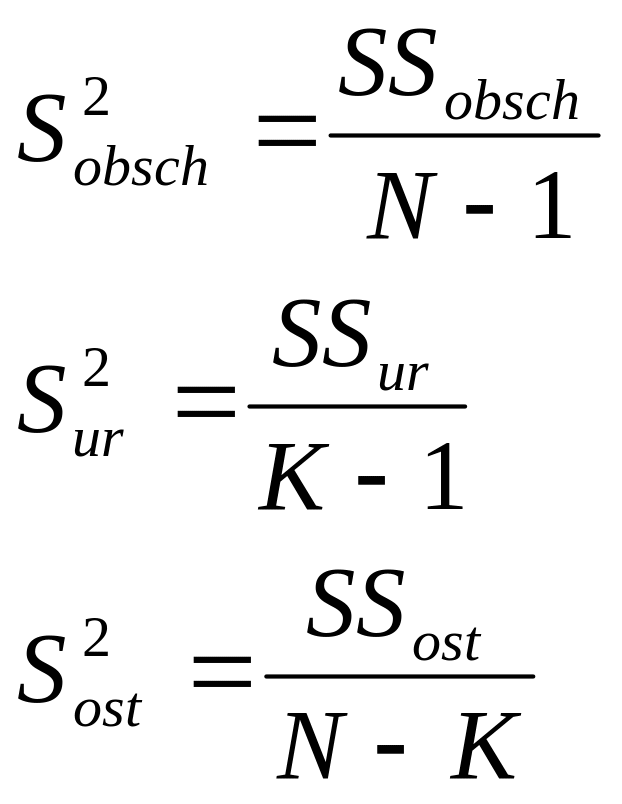
11.Статистическая обработка результатов дисперсионного анализа

Для статистической обработки результатов дисперсионного анализа используются методы проверки статистических гипотез. При решении задач такого рода проводится проверка статистических решений о параметрах генеральной совокупности выбранных моделей.

Всякое предположение о генеральных параметрах или о типе модели называется статистической гипотезой. Проверка статистической гипотезы осуществляется на основе выборочных данных. При этом ищется ответ на вопрос: «согласуются ли выборочные данные с гипотезой или нет».

Обычно гипотеза выдвигается относительно параметров, которые могут иметь одно или несколько значений. Одно значение – простая гипотеза, несколько – сложная. Правило, по которому отвергается или принимается гипотеза – критерий проверки.

Модель дисперсионного анализа может быть представлена следующим образом:

- математическое ожидание генеральной совокупности,

- эффект j-го уровня признака классификации,

- частное математическое ожидание генеральной совокупности для j-го уровня,

- ошибка наблюдения.

Выдвигаем нулевую гипотезу . В двухфакторном ДА альтернативная гипотеза не рассматривается.

Рассмотрим, какие статистики используются в качестве критерия проверки гипотезы. Они основаны на статистике выборочной оценки дисперсии, которая подчиняется распределению хи-квадрат. Из математической статистики известно, что распределение выборочной дисперсии как СВ имеет теоретическое распределение хи-квадрат, зависящее от числа степеней свободы и уровня значимости ил и доверительной вероятности.

Для проверки статистической гипотезы в ДА вычисляют оценки двух дисперсий: общей и дисперсии уровней.

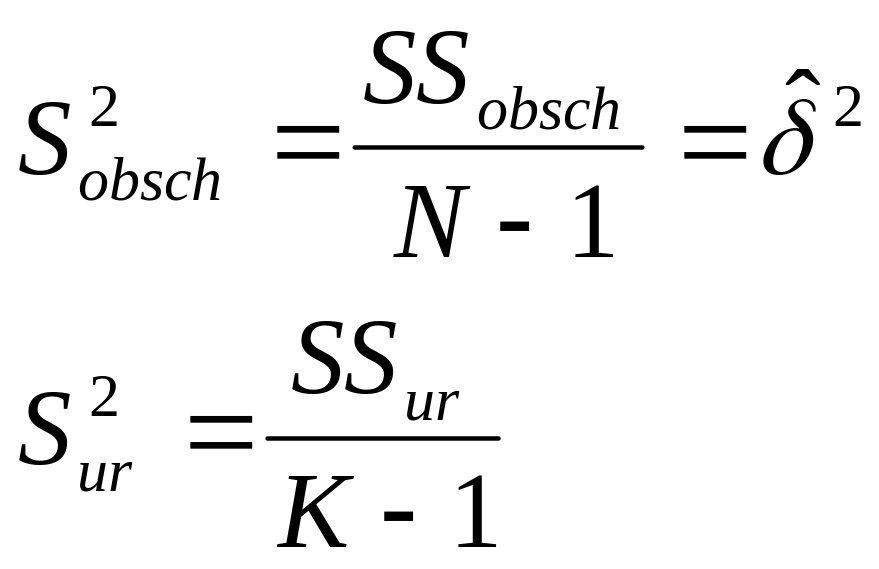
Если различия между группами классификации отсутствуют, то оценка дисперсии уровней будет такой же, как и общей, и остаточной дисперсий:

Чтобы сравнивать дисперсии между собой используется отношение дисперсий. Известно, что эта статистика имеет распределение Фишера. Использование статистики Фишера и его распределения позволяет проверить статистическую гипотезу о равенстве двух дисперсий.